Departments:
  1. Communication Engineering
Softwares:
  1. MATLAB

Convolution calculator in matlab
Hello friends, hope you all are fine and having fun with your lives. In today's post, I am gonna design a Convolution Calculator in MATLAB. We all know about convolution but if you don't know then here's the wiki page for convolution which has a detailed description of Convolution. In simple words, convolution is a mathematical operation, which applies on two values say f and g and gives a third value as an output say v. In convolution, we do point to point multiplication of input functions and gets our output function.

Convolution is an important technique and is used in many simulating projects. It has a vital importance in image processing. So, today we are gonna do convolution in MATLAB and will check the output. You should also check Image Zooming with Bilinear Interpolation in MATLAB in which we have used correlation technique which is quite similar to convolution. It will give you a better idea of convolution, I recommend you to read their difference. Anyways, coming back to our today's Convolution Calculator, let's start its designing:

Convolution Calculator in MATLAB

  • MATLAB has a built in command for convolution using which we can easily find the convolution of two functions.
  • Syntax of this builtin convolution command is v=conv(x,h) where x and h are the input functions while v is our output.
  • In my code I have used this builtin function as well as I have also design a small algorithm for calculating the convolution using its formula.
  • After finding both the convolutions, I have simply compared them by plotting them on graph so that we can also verify that our result is correct.
  • You can use this convolution calculator to find convolution of any two functions.
  • So, first of all, copy this code and paste it in your m file and run it in your MATLAB:
clc
close all
clear all


x=input('enter the sequence, x(n)=')
h=input('enter the sequence, h(n)=')

m=length(x);
n=length(h);
subplot(4,1,1)
stem(1:m,x,'fill','r')
grid on;
title('input sequence, x(n)=')
xlabel('time n------>')
ylabel('amplitude----->')

subplot(4,1,2)
stem(1:n,h,'fill','r')
grid on;
title('impulse sequence, h(n)=')
xlabel('time n------>')
ylabel('amplitude----->')
%------linear convolution using inbuilt command------------------------%
v=conv(x,h)
l=m+n-1;
subplot(4,1,3)
stem(1:l,v,'fill','r')
grid on;
title('output sequence using inbuilt command, v(n)=')
xlabel('time n------>')
ylabel('amplitude----->')
%--------linear convolution using 'for' loop------------------------------%
X=zeros(1,l);
H=zeros(1,l);
X(1:m)=x;
H(1:n)=h;
for i=1:l
    Y(i)=0;
    for j=1:i
        Y(i)=Y(i)+X(j)*H(i-j+1);
    end
end
Y
subplot(4,1,4)
stem(1:l,Y,'fill','r')
grid on;
title('output sequence using loop, Y(n)=')
xlabel('time n------>')
ylabel('amplitude----->')
  • The above code for convolution calculator is quite self explanatory but let me explain it a little.
  • First of all, I am asking for inputs from user and they are saved in variables named as x and h.
  • After that I am plotting them using stem function.
  • In the next section, I have used the default MATLAB command for Convolution and calculated the convolution of x and h and saved it in v.
  • Next I applied my simple algorithm and calculated convolution of x and h and saved it in Y and also plotted it.
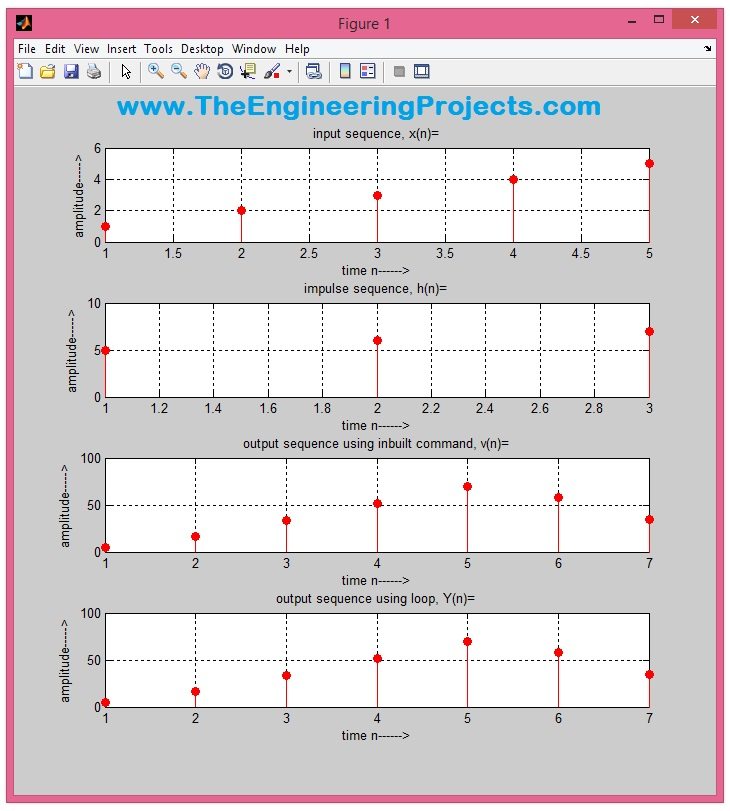
  • Once you run the simulation and give your input functions, you will get the below results:
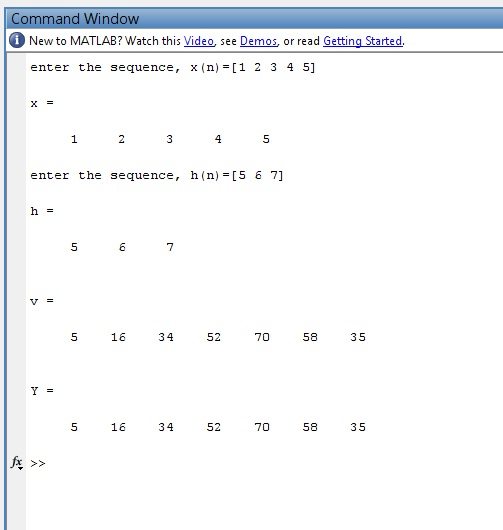
Convolution calculator in matlab,Convolution calculator, convolution in matlab, convolution code in matlab, matlab convolution code
  • You can see in the above figure that I have given two inputs x and h and MATLAB Convolution Calculator calculated the convolution and gave us v and Y.
  • v is calculated by default MATLAB command while the Y is calculated by our small convolution algorithm.
  • Their graph representation is shown in the below figure:
Convolution calculator in matlab,Convolution calculator, convolution in matlab, convolution code in matlab, matlab convolution code
  • You can see in the above figure that we have plotted all the four signals, two inputs and two outputs and you can see both the outputs are same.
  • Here's the video for this convolution calculator in MATLAB:
That's how you can design a convolution calculator in MATLAB. Let me know about your experience with this convolution calculator. I am planning to design a GUI for this calculator and will add it in this post.