Hello learners welcome to the next tutorial on MATLAB where we are learning about this excellent environment in detail without skipping anything. Last time, you have seen the data types and their detail through practical implementation and this time, you will get information about the operators used in MATLAB and the text-related information in an efficient way. By the end of this lecture, you will be able to answer the following questions:
What are the operators and can we use operators in MATLAB?
How can you implement the arithmetic operators in your MATLAB?
What is the significance of the relational operator?
What is the detail of the logical operators in MATLAB?
What are bit-wise operators?
How can you give a brief introduction to the short circuit operators?
All of these are important questions not only in programming in the MATLAB language but this is also related to other mathematics and related fields. In order to understand well, I’ll suggest you open your MATLAB software and practice every case on your own because it is super easy to work with the operators in MATLAB even if you are new to this programming environment.
Introduction to Operators in MATLAB
An operator is a symbol that instructs the compiler to perform numerical or logical operations. MATLAB is designed to work primarily with whole matrices and arrays. As a result, MATLAB functions can operate on both scalar and non-scalar data. For a detailed introduction, have a look at the statement given next:
"The term operator refers to a symbol in computer programming and mathematics that is used to perform specific logical and mathematical operations. It can also be defined as a personification of an action."
So, we can say, you have used the operators knowingly or unknowingly hundred or thousands of times in different software and today, we are just relating all the procedures to MATLAB and will learn what can we do with these operators.
As we have used the basic operations on the matrix many times so, we will be more involved in a little advanced example this time.
Using Operators in MATLAB
The procedure to use different operators is somehow the same as in the real life when we use them in our notebook in mathematics or related subjects. Basically, we divide the operators in MATLAB into the following categories:
Arithmetic operators
Relational operators
Logical operators
Bitwise operators
All of these will be discussed in detail and we believe that most of them are known to you so for your practice, we will have more focus on the examples of each case. In addition, you can also make your own matrices and arrays in addition to my example to have fine practice and it is also fun.
Arithmetic Operator
The first and the easiest operator is, as you can guess, the arithmetic operation in which we use the basic operations of mathematics through these operators and therefore, this will be easy for you to understand. But here, the new thing is, the arithmetic operations are categorized into two classes:
Matrix arithmetic operators
Array arithmetic operators
The introduction of both of these are self-explanatory but when we talk about the difference between them, we come to know that if the operator is applied to the matrix then it is the matrix arithmetic operation and vice versa. Another point that differentiates between these two is, we use array arithmetic operation, then we use a dot between the symbols of the array to highlight the procedure. The detail of each operator is now given below:
Addition Operator
As you can guess, this operator is denoted by a plus sign between the two values to be added and it is the simplest and most frequently used operator. The condition is applied on this operator according to which, both the values (either in MATLAB or simple additional values) must be of the same size if they both are vectors otherwise, if one quantity is a scaler, then it will be added to every member of the matrix.
Subtraction Operator
The subtraction operator is the same as the subtraction in the real world done by us. It also follows the same condition as the additional operation. But you must know, it also includes the negative values in it because many times, the larger value is subtracted from the smaller one we get the negative values in matrices or arrays.

Matrix Multiplication Operator
Here comes a slightly different operator than the simple arithmetic operation of the daily world. We can use this operator if and only if the number of rows of one matrix is equal to the other to be multiplied. Otherwise, the same as the other operators, the results are impossible to get.
If A and B are two matrices then C, which is the resultant of the multiplication can get as
C=A*B
The reason why we are checking the formula of this operation will be clear to you when you will read the next section.
Array Multiplication Operator
There is a bit of difference between this operator and the one discussed before. In this case, each and every element is multiplied by the corresponding element of the other. It is denoted by the dot between the signs of the matrices.
If we take the same example as given above, we will denote the array multiplication as:
C=A.*B
Matrix Right Division
The right division of the matrix can be explained well with the help of the example that if A and B are two metrics then their right division is obtained by the following expression:
C=B/A=B*inv(A)
Array Right Division
Just like the array multiplication, the array right division method includes the dot sign between the arrays and we can understand this concept while looking at the expression given next:
C=B./A

Matrix Left Division
Let’s say that if A is the nth order matrix and B is a single column metric then their division, denoted by C=A\B is equivalent to CA=B.
Array Left Division
In this type of MATLAB operatorA.B is the matrix with elements B(i,j) a(I,j), where A and B must be the same size.
Power of the Matrix
The power of the Matrix is obtained when each Element in the matrix is multiplied by itself equal to the number of the power written just at the upper right corner of the matrix. You can perform this operation by using the A^n sign where n is the power of the matrix.
Transpose of the Matrix
You know the transpose of the matrix and its procedure. But in MATLAB, it's more simple and you can easily get the transpose of the Matrix by Using the A’ command where the A is a matrix.
Relational Operations in MATLAB
A relational operator determines the relationship between each element and two arrays. If a relation exists, the value is returned as true or false.

The operator returns an array of the same size with the values true or false depending on the outcome of an operation. These operators can operate on both scalar and non-scalar data:
< is called Less than
<= is called less than equal to
> is the sign of greater than
>= is a sign greater than or equal to
== can be stated as equal to
~= refers to not equal to
Logical Operations in MATLAB
The logical operations are somehow different from the first two types. In these types of operations, only two possibilities are there. Either you get 0 or 1. We hope you are aware of the boolean expressions and by connecting the discussion with them, we get the idea that:
"The logical operations in MATLAB follow the logic of the boolean operations and therefore, the results in such calculations are always either 0 or 1 and therefore, we get the true or false conclusion."
If we talk purely about MATLAB, we come to know that there are three types of logical operators and functions listed below:
Element-wise logical operations
Bit-wise logical operations
Short circuit logical operations
Element-Wise Logical Operations
These are the operations that take the elements of all the cases and perform the procedures separately. Three types of procedures are listed in this type and operators used for different processes are & (AND), |(OR), and ~ (NOT). Moreover, XOR operation is also included in the same category. This will be clear when you will see the representation and the quick revision of the results related to these operators. Suppose we have two elements with the following values:
X=[0 1 1 0 1];
Y= [1 1 0 0 1];
Then, the result of each element-wise logical operation will be:

Operator Name |
Symbol |
Description |
Result |
AND |
& |
It gives the value 1 only if both the elements are one, otherwise gives zero. |
X & Y= 01001 |
OR |
| |
It gives the value 1 every time when any of the elements are one, otherwise gives zero. |
X | Y = 11101 |
NOT |
~ |
It gives the opposite result all the time and it is a unary operation. |
~X = 10010 |
XOR |
⊕ |
It gives the value 1 every time when the elements have the same value. If they have opposite values, then it is always zero. |
X⊕Y=xor(X,Y)=10100 |
One thing that has been noticed here is, as we said earlier, the values in the logical functions are always 0 and 1 therefore, we have also used only these two numbers in the elements and got the results with the same results.

I hope you now have the best idea about the calculations. Let’s move towards the next type.
Bit-Wise Operator
The bit-wise operation, as the name suggests itself, is used when there is a need of bit by bit calculations. Same as in the previous case, the functions are shown with the help of signs and by looking at the table explained below, you can get an idea of the working of each operator.
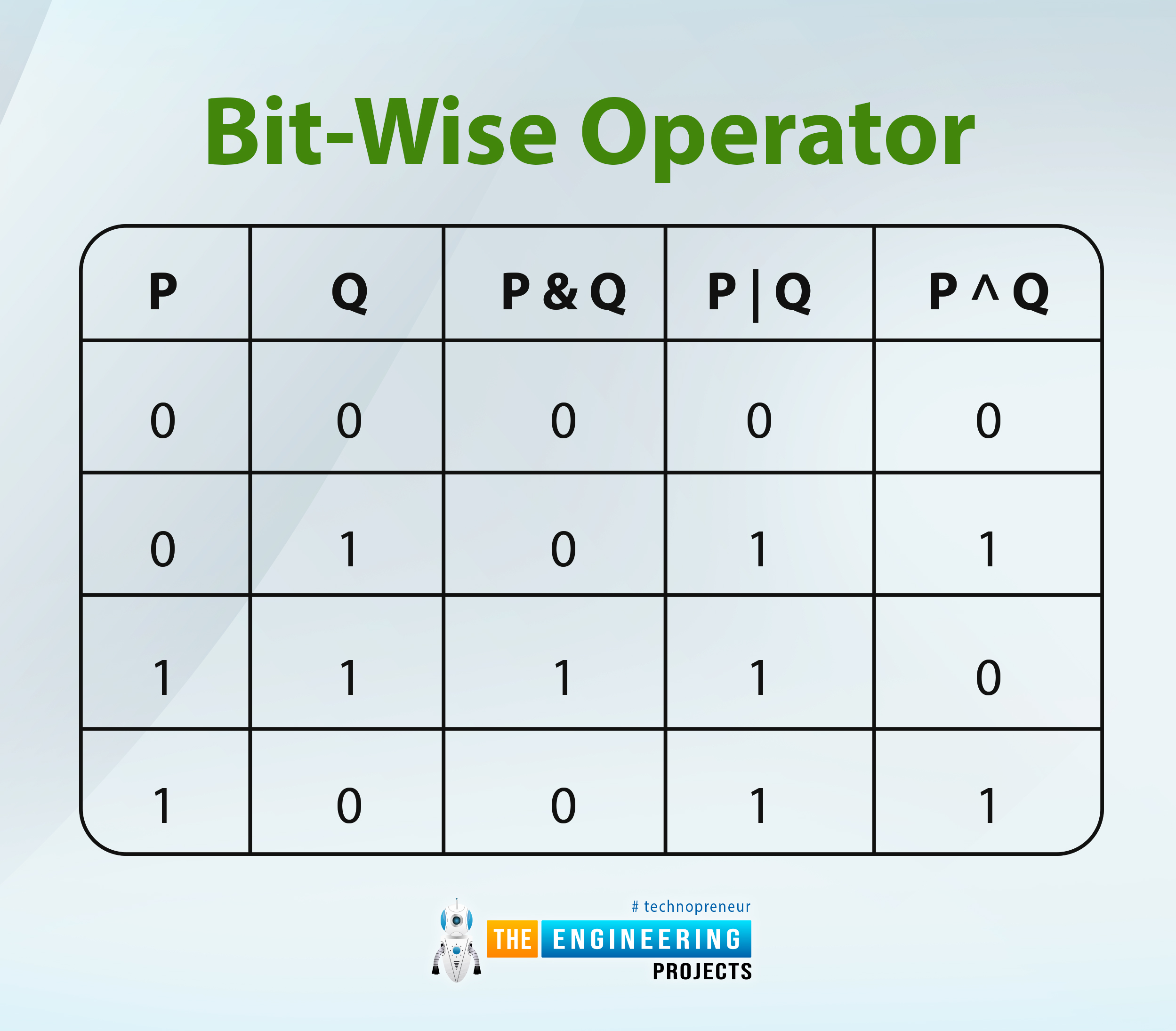
P |
Q |
P & Q |
P | Q |
P ^ Q |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
Matlab provides the following bitwise operators:
bit and (a,b) – Bitwise AND (integers a and b).
Bitmap (a) – It is used to bitwise the compliment of a.
Bitget (a , pos) – Get bit at a specified position, in the array a
Bitset (a , pos) – set bit at a specified location of a
bitShift (a,k) – It is used to get the equivalent results as multiplied by 2k. Therefore, if k is negative, it shifts right, on contrary to this, if k is positive, it shifts to the left position.
bitor(a, b) – The operation of this operation is Bit-wise XOR of integers a and b
Short Circuit Operator
In addition to the general operator describe before, we have some more interesting operators as well. The operators listed below perform AND and OR operations on logical expressions, including scalar values. They are short-circuiting operators because their second operand is calculated only when the first operand does not fully determine the output.
&&
It gives the value of 1 only if both operators give the result 1 otherwise it is zero.
||
It gives the value 1 if either or both inputs are one. We get the contrary results otherwise.
Trus, we have seen a lot of operators today that are helpful to understand the introduction of the operators in MATLAB. Many of these have the same symbol and representation of the operators and results. We have seen arithmetic operators, relational, logical, bit-wise, and short circuit operators. It is important to mention here that other operators such as set operators are also included in this learning but I have not mentioned them because these are less known and less used operators in MATLAB. We’ll discuss them in some other tutorial. For now, it is enough to have this information and your homework is to perform all the remaining operators that I have not shown you in MATLAB.







































 MATLAB
MATLAB syedzainnasir
syedzainnasir 0 Comments
0 Comments

















