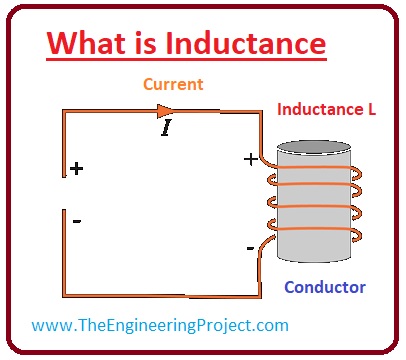
What is Inductance

In today’s tutorial, we will discuss What is Inductance. In 1886 first time in the world the word inductance was used by the English scientist Oliver

Posted at: 10 - Oct - 2019

Category: Tutorials

Author: zahidali

0 Comments

Hello friends, I hope you all are doing great. In today’s tutorial, we will discuss What is Inductance. In 1886 first time in the world the word inductance was used by the English scientist Oliver Heaviside. The symbol for the inductance is L that was indicated due to the scientist Heinrich Lenz who gave famous Lenz's law. In system international (SI) the unit of the inductance is Henry. It can be defined as if one volt is provided to the coil and 1A current passes through coil than flux induced in the coil is one weber the inductance of the coil will be one Henry. Henry name is used due to American scientist Joseph Henry who find the phenomena of the self-inductance. In today's post, we will have a look at different parameters of the inductance and its working. So let's get started with What is Inductance.

What is Inductance

Inductance is the property of any conductor due to that it resists any variation in the current passing through it.
The current passing through the conductor generates the field about it, the magnitude of the field depends on the strength of the current.
The variation in the magnitude of the field, with the variation in the current, produce emf in the conductive element, this emf resists the voltage that is varying the current.

Inductance can also demonstrate as it is the multiple of the ratio of the voltage produce with the variation in the current.

V = -L(di/dt) V

Inductance is of two types first one is the self-inductance and second is mutual induction.
If current passing through any inductor induced a voltage in that conductor is known as the self-inductance.
If voltage induces in the second conductor that is closer to first then this phenomenon is known as the mutual induction.

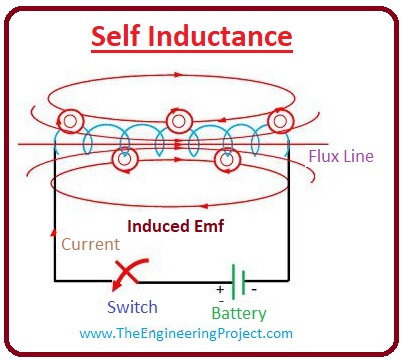
Self Inductance

When current moving through the current induced voltage in that conductor it is known as the seld inductance.

L =N(ø/I)

In this equation.
- L is the self-inductance of the conductor.
- N is the no of turns.
- ø is the flux.
- I is the current flowing through the conductor.
Due to the flux induced in that conductor, current variation produced electromotive force in this conductor.
Due to this electromotive force, there is another current produces in the current in reverse direction of the current supplied by the external power source.
The variation in this current resists the alteration in the first current.
If the value of the first current is enhancing, the second current will resists the increment in the first current.
The overall effect of this is to minimise the magnitude of the alternating current flowing in the inductor and also eliminate the magnitude of the voltage provided to the conductor.

Mutual Induction

If the current is passing through the one coil and its flux also linking with the nearby second coil than due to variation of the flux voltage induced in the 2nd coil this phenomenon is known as the mutual induction.

For a practical understanding of the mutual induction, let's discuss the given figure.
There are 2 coils X and Y are located closer to one another. When we close the switch current starts to flow through the coil X and voltage induced in that coil.
The flux of the coil is also linking with the Y coil, if we vary the current at X coil there will be also flux variations in the second coil that induced a voltage in the coil it is due to the phenomenon of the mutual induction.
Now we mathematically find the value of the mutual induction in the two coils.

Em = M (dI1/dt)

M = (Em)/ (dI1/dt)------(A)

This equation is used when we know the value of the induced voltage in the second coil and the current variation in the first coil is known.
If we have the value of the one volts and (dI1/dt) is also one ampere then by adding these values to the equation (A) then we find the mutual inductance that is one henry.
From the above-given equation, we can explain mutual inductance as, if one volt is provided to the first coil and current passing through the second coils is at the rate one ampere per second then it has a mutual inductance of one henry.
Mutual induction can also be described in by this equation.

Em = M(dI1/dt)= d/dt (MI1)--- (B)

Em =N2(dØ12/dt)= d/dt (N2Ø12)---(C)

By using equation B and C we have.

MI1 = N2Ø12

M = (N2Ø12 /I1)

This equation of the mutual induction can work only when the flux interaction with the second coil (N₂f₁₂) due to the current (I1) of the ist coil is already known.
From the above-given equation of the mutual induction, we can conclude that it depends on these given below factors.
- No of the turns in the second coil.
- Area of the coils.
- The distance among the coils.

Energy Stored in an Inductor

Now we discuss the phenomena of energy storing in the inductive coil.
The energy stored in the inductor in the form of the magnetic field.
The field of the inductor is directly proportionate to the current provided to the inductor.
Given below formula explains the energy stored in the inductor in the form of the magnetic field.
E = 1/2 LI²
In this equation.
- E is the amount of energy stored in the inductor.
- L is the self-inductance of the conductor.
- I is the current passing through that conductor.

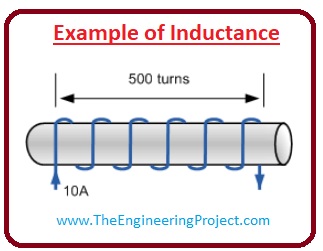
Example of Inductance

In the given diagram, the coils have five hundred no of turns, and it is made by the cooper.
When we applied ten ampers of direct current to the coils then the flux of ten milli-weber is produced in that coil. Now we find the value of the self-inductance.
As we know that the formula for the self-inductance is.

L =N (Ø/I)

If we put the values of the no of turns, flux and current then we have inductance value.

=500x (0.01/10)

= 500 milli-henry

It is the detailed article on the inductance I have written almost each and everting related to the inductance in this post. If you have any question ask in comments. Thanks for reading.