

Classification of Systems

Hello Pupils, We are learning about signals and systems, and till now we have learned some basic information regarding signals, but we know a little about systems till now. We have learned about the system in our previous lectures. To have a clear concept, we have arranged this tutorial in which we are studying the systems and their classification. Have a quick glance at today’s topics:
What is a system?
What are the various types of systems?
What is the principle of homogeneity?
What is the principle of superposition?
How can we compare each type while keeping their differences in mind?
To keep things simple, we’ll also have examples of some of these signals. Yet, the first thing that we are going to do is to revise the basic definition of the system so that we may move forward.
What is a System in Signal and Systems?
A system is a closed connection between the input signal and the output. All the procedures and techniques required to convert the input into output are called the system, and if we talk critically, then the basic definition of a system is:
“A system is a collection of components that, when interconnected, provide a signal that is proportional to the signal that was fed into the system.”
To understand, keep in mind, that the system has the input where the data is fed, then different procedures take palace on that data, and as a result of this procedure, we get the output from the system.

Classification of Systems
As with signals, systems also have some types, and these types are clearly classified for convenience. We will go through some basic types and will try to have a clear concept through discussion and examples.
Linear and Non-Linear System
There are different ways to define the linearity of the system, but the easiest one is, that a system is called linear only if it follows:
Principles of homogeneity
Principle of Superposition
We’ll define both of them one after the other in detail.
Principles of Homogeneity
According to the concept of homogeneity, a system that produces an output y(t) for an input x(t) must also provide an output ay(t) for an input ax. This is the condition that must be met for the system to be considered homogeneous (t).
Principle of Superposition
According to the concept of superposition:
“A system that produces an output of y1(t) for the input of x1(t) and output of y2(t) for the input of x2(t) must create an output of [y1(t) + y2(t)] for the input of [x1(t) + x2(t)]. Similarly, [y1(t) + y2(t)] for the input of [x1(t)], and implies any number of different signals in the system. "
Well, is it confusing? Do not worry because we are discussing it in simple words. Consider the case when the system has more than one signal in it. If we provide it with 3 signals (let’s say) at the input, then the output contains the collective effect of all the signals that we were expecting from each and every signal by adding them.
It may make no sense at the time because every person, after using their commonsense, can make this decision on their own, but keep in mind that these types of principles are highly effective in solving the complex problem of calculations.
As a result, when we plot the graph of a linear system, we find a simple and clear graph that is usually straight in line. It is the reason behind calling them “linear”. It is usually easy to deal with the linear system as compared to the other type that is non-linear. The reason behind this will be discussed in just a bit. Before that, have a look at the diagram given below:
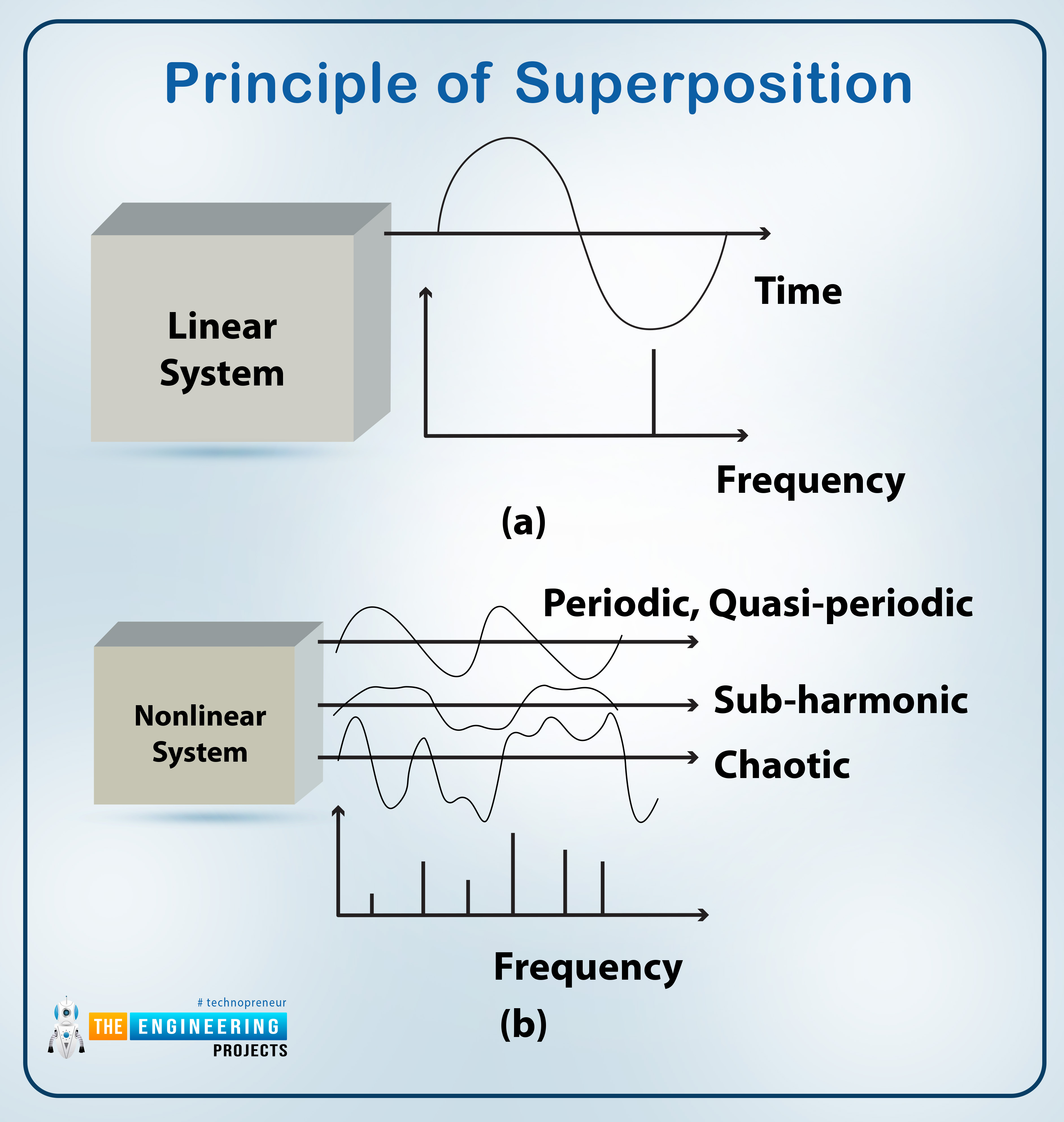
Non-Linear System
On the other hand, if the system does not obey the principles of superposition and homogeneity, then it is called non-linear. It is not possible to develop a general differential equation of finite order that can be utilized as the mathematical model for all systems when dealing with nonlinear systems; this is because such an equation would be impossible to solve. This is due to the fact that there are numerous distinct paths via which nonlinearities might emerge, and these paths cannot all be mathematically expressed using the same form. In addition to this, it is essential to keep in mind that the concept of superposition cannot be applied to nonlinear systems.
Continuous-Time System
Let’s talk about a very simple and obvious type of system. A system is called a continuous-time signal if the input given to it, and the output obtained from it, both are continuous-time signals. The operations done on the input do not change the form of the input signals and hence the output is not affected in its shape and type.
Example
A simple example of a continuous-time signal is an amplifier in which the input is analog in the form of voice. Different procedures occur inside the system (amplifier), and from the output, an amplified voice (analog signal) is obtained from it.
Discrete-Time System
As you are expecting, a discrete-time system is one in which the input given to the system and the output obtained from the system, after different procedures, are in the form of discrete-time signals. If in any case, the system changes the signal from discrete to continuous, then it will not be a discrete-time system.
Example
Micro-processor is an example of a discrete-time signal because all the processes that occur in the micro-processor are based on just two numbers that are zero and one and the output, after different operations, remains in the same format.
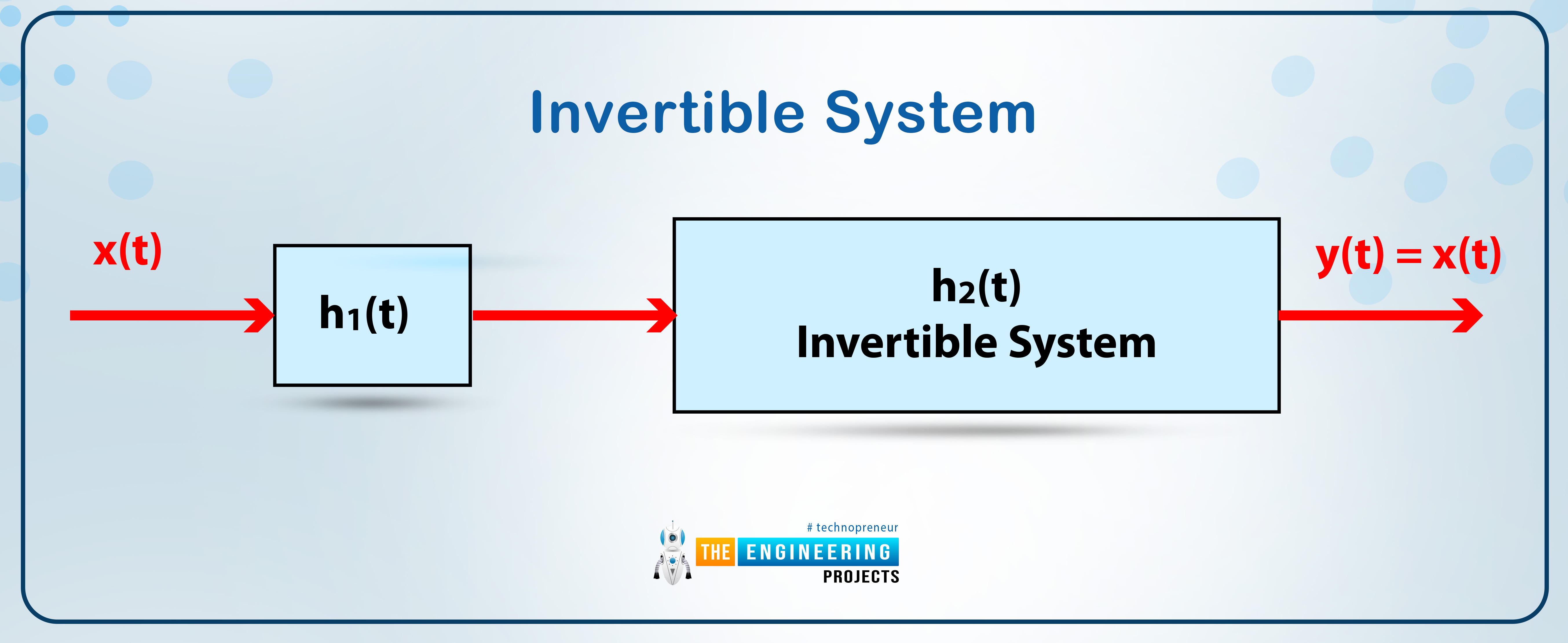
Invertible System
In some cases, the same results can be obtained from the output of the system that was fed into its input signal, and such systems are termed invertible systems, as the name implies. We define them as:
“A system is said to be an invertible system if it is designed in such a way that the input, that is fed into the system goes through some changes and these changes can be converted into the original signal again by using the different procedure and the input is equal to the output.”
Practically, an invertible system is obtained by using a system in which, in addition to the simple system, an inverter or any other device, that has the opposite mechanism is cascaded to obtain the same input and output.
Non-invertible System
The system in which the input and output are not equal is called non-insertable. We define them as:
“A system is said to be non-invertible if the effect of the system, exerted on the input signal, can not be inverted. No matter which procedure you are following inside the system, you will get different inputs and outputs. “
Time-Variant Systems
Time-Variant systems are those whose output depends upon time. We know that every signal has time on the x-axis but keep in mind, in a time-variant system, a signal depends upon the change in time.
Example
The example given below represents the case of a time-variant system:
y(n)= x(-n)
Time-invariant System
The system is said to be time-invariant if the output of the system does not depend upon the time of the system.
Example
Consider an example in which the output is called y(t) and the input is represented as x(t). Then the equation given below presents the time-invariant system:
y(t)=x(t)+x(t-1)
Static System
Here is another type of system. We all know that static means motionless or unchanging condition. A static system is one that depends upon a particular result at a particular time and it does not have any relationship with the previous or future results.
“A static system is the one that depends upon the present situation only and does not have any mechanism to store the past or future value because it does not need to store these values”.
Example
𝑐(𝑡) = 𝑟(𝑡)
𝑐(𝑡) = 2𝑟2(𝑡)
In these examples, the whole system depends upon the time at a particular instant, and it does not have any concern with the previous or upcoming value. This will be more clear when you look at the example of the dynamic signal in just a bit.
Dynamic System
Dynamic means anything that is not stationary. In the case of signals, the dynamic signals are the ones that depend upon the present, past, and future values of the signals. Have a look at the definition:
“A dynamic system is one that can not be achieved by using the present values of the signals only; instead, they also depend upon the future and past values, and therefore, they require memory to store the previous results."
Example
A simple example of a dynamic system is the capacitive system. The capacitor is used to store the charges, so they are also used to store the memory in computers, and the discharging process depends on the number of charges stored an instant before. Therefore, we consider it a dynamic system. More examples are inductive circuits, delay circuits, accumulators, etc.
Casual System
Have a deep look at these signals. These are the ones that totally depend upon the present and past values of the signal but do not have any concern with the future values.
Keep in mind, that these are not the same as the static or dynamic system, but are slightly different from them.
Non-casual System
In non-casual systems, the system depends upon the past, present, and future values, and if any of them is missing, the system is not able to work properly.
Summary
We are going to end by discussing the summary of the whole article. We have ready many types of signals and, similarly, systems also have some classification. Most types of systems have an opposite type as well and for convenience, we have discussed them one after the other so that you may compare them and have a clear idea about them. We have discussed some common types of systems and the key points of each type are given below.
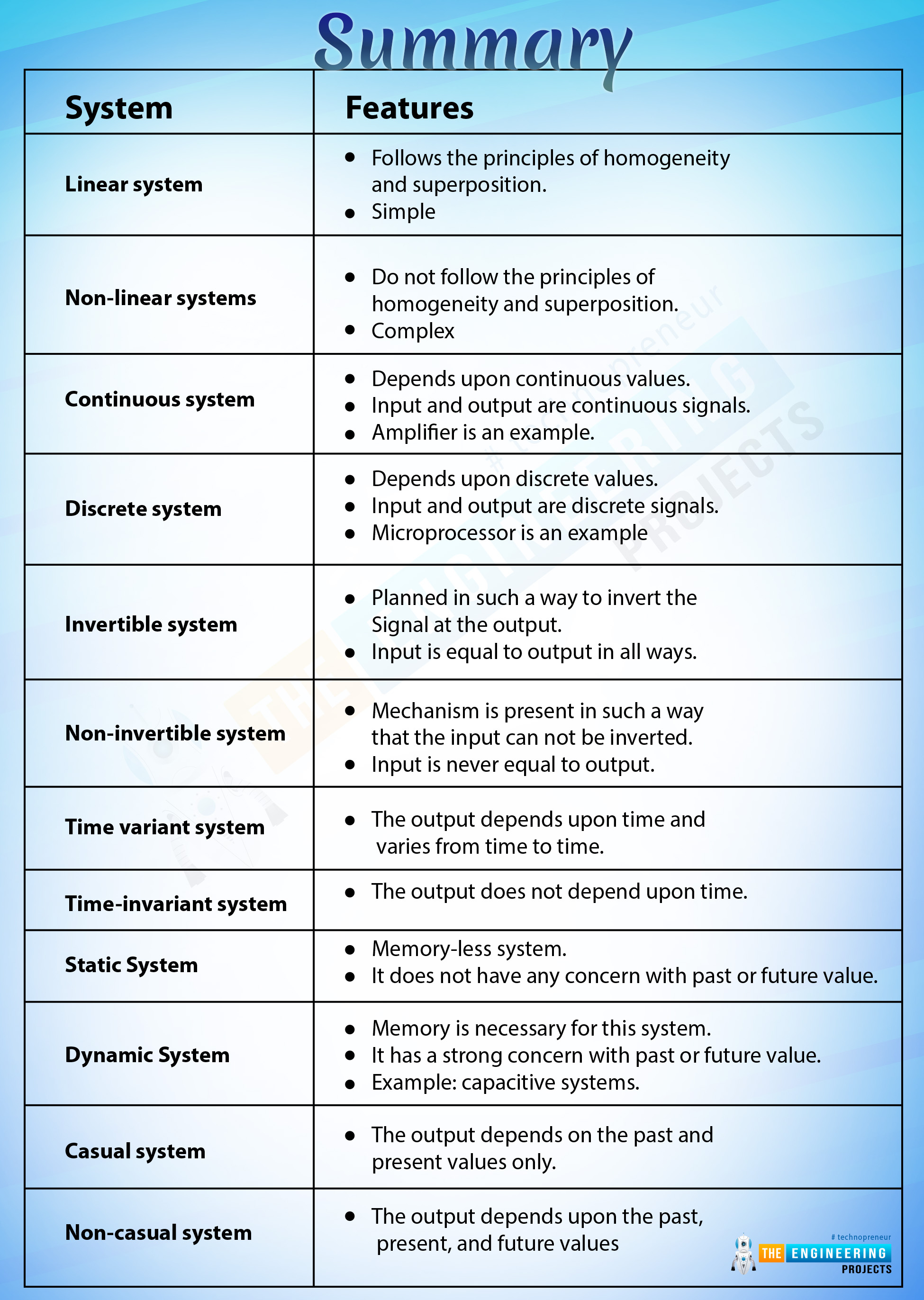
System |
Features |
Linear system |
|
Non-linear systems |
|
Continuous system |
|
Discrete system |
|
Invertible system |
|
Non-invertible system |
|
Time variant system |
|
Time-invariant system |
|
Static System |
|
Dynamic System |
|
Casual system |
|
Non-casual system |
|
Conclusion
There are numerous types of systems in which the type of input and the type of output are strongly examined to know the particular type of system. For the best understanding, keep the difference between each of them in mind. There may be other types as well yet for this course, these types are more than enough. You should go through them and find the examples of each of them by summing up your concepts and common sense. You must keep in mind, that a system can be of more than one type at a time. We will go through the next topic in the next step.








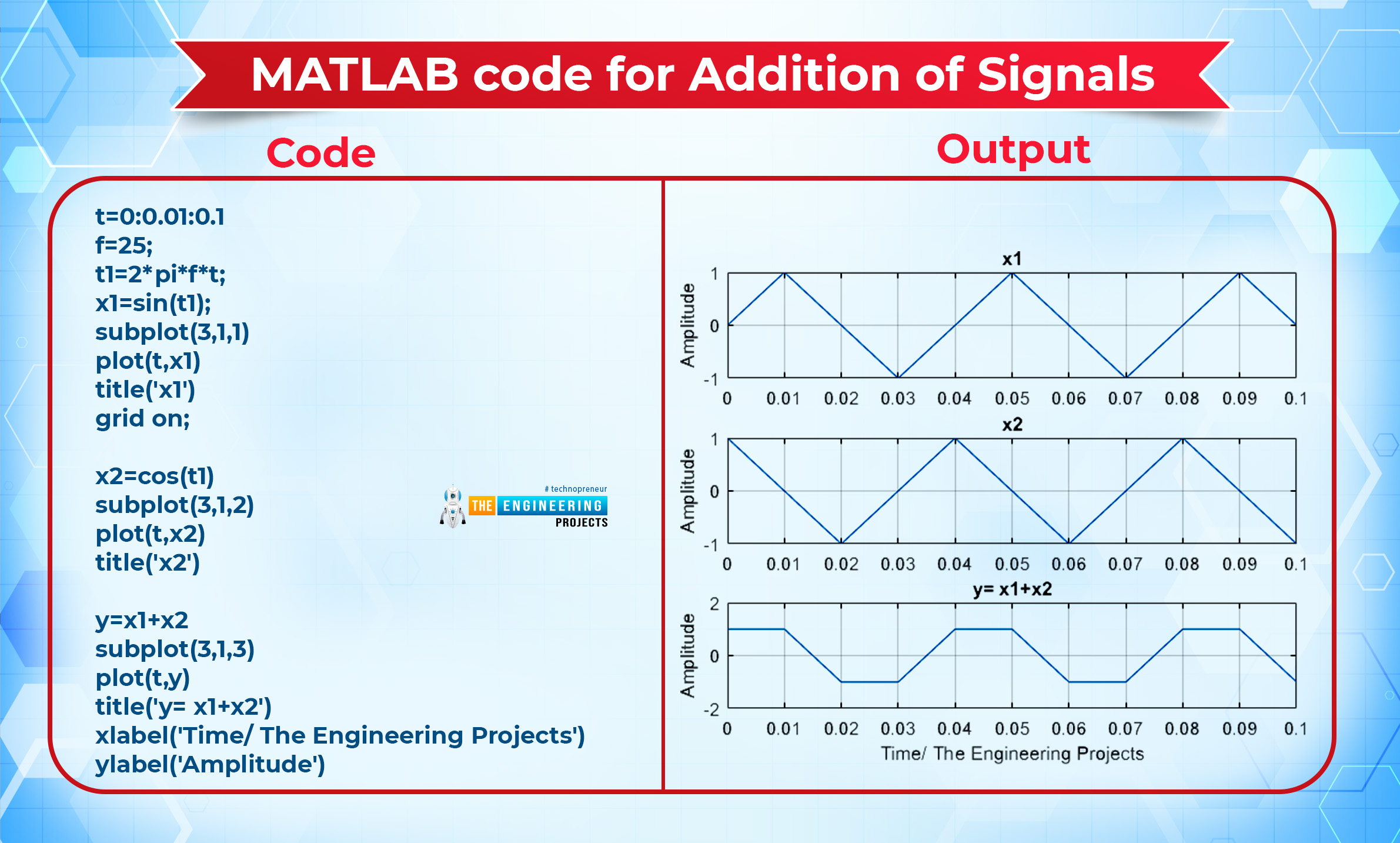
 MATLAB
MATLAB
 0 Comments
0 Comments















 basics of systems
what is system
system in singal and systems
types of systems
invertible system
basics of systems
what is system
system in singal and systems
types of systems
invertible system
 Wednesday, August 31, 2022
Wednesday, August 31, 2022 Prev Page
Prev Page






 RSS
RSS
 YT
YT
 FB
FB
 TW
TW




















