Properties of z-Transform in MATLAB

Hello, readers. Welcome to another lecture on signals and systems where, on the previous day, we studied the transforms. A Z transform is used to change the domain of a signal or function. It is used to convert the signal from the time domain into the z plane. Now we are going a little deep into the discussion. Have a quick promo of the topic of today:

• What are the properties of z transform?

• What is the unit impulse of z transform?

• What is the unit ramp of z transform?

• What is the difference equation and how is it related to the z transform?

• What are some important applications of z transform?

We’ll go through each of these topics in detail, so stay with us to learn about all of them.

Properties of z Transform

Till now, we have seen the introduction of z transform along with some basic information. It's time to discuss some properties of z transform in this lecture. We always mention the properties of the topic if possible to clearly describe the nature and workings of that particular topic. It will be correct to say that while discussing the properties of a mathematical tool, we provide you with a wide domain of learning and experimenting about that particular topic. 

Linearity of the z transform

The z transform is always linear. It means, if we have two statements and apply the z transform individually on both of them, then we always get the linear results. Mathematically,

If

 F(z) = Z{fn}

and 

G(z) = Z{gn}

Then

Z{afn + bgn} = aF(z) + bG(z)

Time Shifting Property

When we talk about the time shifting property of z transform, we come to know that while passing through the time shifting process while we are performing the z transform, we get the following results:

 x(n)⟷Z.TX(Z)

If we take n-m instead of n in the property given above, we’ll find the results in which the signal in the z plane multiplies with the z complex number having the exponential power equal to the m with a negative sign with it. 

Time Reversal Property of z Transform

The time reversal property of z transform states that if we have the following condition:

x(n)⟷Z.TX(Z)x(n)⟷Z.TX(Z)

Then after applying the z transform, we will get

x(−n)⟷Z.TX(1/Z)

You can see that after the application of z transform, we get the z in that is present in the denominator of the resultant X value. Therefore, this property is named the reversal property.

Convolution of z Transform

Convolution is an important process in signals and systems and we have also read great detail about it in this course. While merging the concept of convolution and z transform, we get to know that if, 

x(n)⟷Z.TX(Z)x(n)⟷Z.TX(Z)

and 

y(n)⟷Z.TY(Z)y(n)⟷Z.TY(Z)

Then we can easily guess that 

x(n)∗y(n)⟷Z.TX(Z).Y(Z)x(n)∗y(n)⟷Z.TX(Z).Y(Z)

Keep in mind, the convolution is not same as the multiplication of the signal. It is the process in which two signals are overlapped in such a way that they form the third signal that has a mix of the properties of both the signals that are convoluted. 

Corelation of z Transform

If you have studies about the convolution, you will surely have the information of correlation as well. This property of z transform states that if we have 

x(n)⟷Z.TX(Z)x(n)⟷Z.TX(Z)

and 

y(n)⟷Z.TY(Z)

Then after the process of correlation while you are using z transform, you will get the following results:

x(n)⊗y(n)⟷Z.TX(Z).Y(Z−1)

If you are new to the correlation then you must gpo to our previous lecture about correlation where we have descried this briefly. 

Initial Value Theorem

Based on different experiments and studies, a theorem has been introduced and the initial theorem is one of them. This theorem is used to find the initial value of of the statement without using the inverse z transform and it states that:

x(0)=limz→∞X(z)

This theorem is only applicable to casual signals. 

Final Value Theorem

This is another theorem that is usually introduced while discussing the initial value theorem. It states that if:

x(∞)=limz→1[z−1]X(z)

It is also used in cases where you do not want to apply the inverse z transform and use the alternative way.

Z Transform of Unit Impulse Function

The unit impulse function is used in physics and mathematics. It indicates the function that has zero width and a unit area that is the area of value 1. Unit step function using z transform is simple and easy and it results in the sequential series. Suppose we have the following function:

Then after applying the z transform of this statement, we get a geometric series. Recall that geometric series is the one in which every value is the result of the multiplication of the previous value with a particular constant depending upon the condition given for the geometric constant. 

Z transform and Unit Ramp Signal

A unit ramp function is one that after the implementation of different operations, provides a graph that has a straight slope. Such functions are widely used in the formation of complex operations. While using the z transform, it is defined as:

x(n)=r(n)={n For n≥0 0 For n<0 }

Then we can solve this by using the procedure of z transform as:

Multiplication Property of z Transform

The multiplicative property of z transform is also called the complex convolution property of z transform. It is because, it results by the multiplication of two signals of time domain that corresponds to the complex number of z domain. You can have the idea of this property with the help of the code given nex that is the extension of the code that we have worked with before. 

Z Transform and Difference Equation

The difference equation is somehow a special case in the equation and the z transform is used to solve this in an effective way. It is defined as:

“The difference equation is the special type of equation in which there exists a difference (minus operation) of different variables. These show the relationship between an independent variable and the consecutive difference of a dependent variable.

These are not complex equations, and usually they depend upon arithmetic operations. Here is a simple example of the difference equation:

y(n)− 34y(n−1)+y(n−2)=x(n)+x(n−3)

Another example of the difference equation is:

𝒚-(𝒏+𝟐)−𝟔𝒚-(𝒏+𝟏)+𝟗𝒚-𝒏=𝟐^𝒏

There are certain steps that are used to solve the difference equation, and these are given next:

• Convert the difference equation into the algebraic equation using the specific procedure of the z transform. 

• Calculate the solution of the resultant equation in the z domain. 

• Take the time domain equation of the result by using the inverse z transform (that we learned in the previous lecture).

Difference Equation in MATLAB

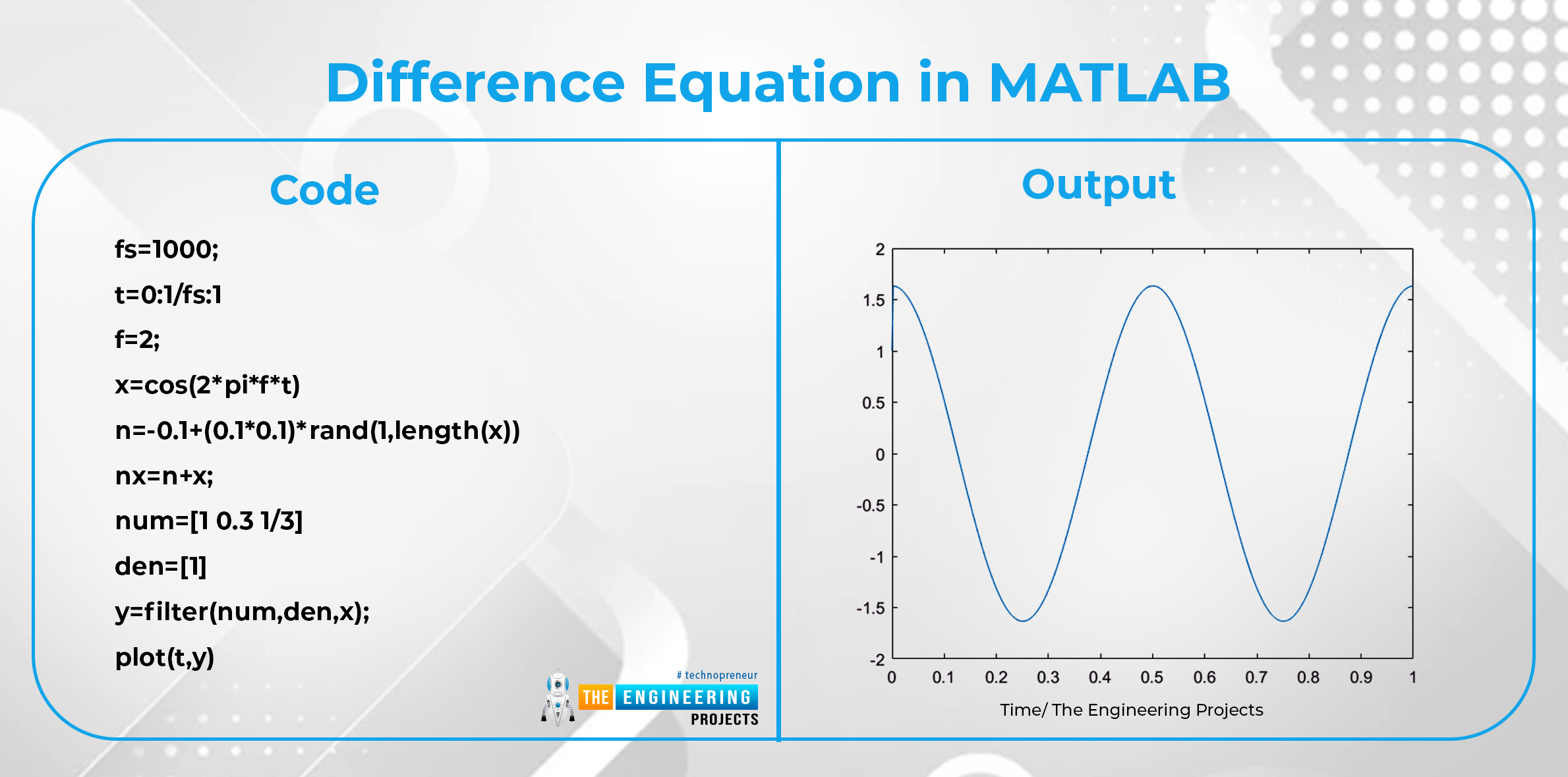
Here, you can see that we have used the plot command to see the signal graphically. You can skip it if you want to have the numerical values only. By changing the frequency value, you can have different types of results. Other parameters that qwe have used are the same that we have described in the previous sections of this series. 

Applications of z Transform

Z transform has great significance in the mathematical field, especially in the signal and system and other branches where the signals have a fundamental role. Till now, we have learned a lot of things about this transform and therefore, we expect that you will understand the reason why this transform is used in almost every field of mathematics. 

Analysis of Digital Filters

As we have said earlier, z transform deals with discrete-time signals. This is the main reason z transform is used in the process of digital filter analysis. The interesting fact is, laplace transform can not be used in this regard because they can not work on the discrete signals. 

The digital filters are the mathematical algorithms that are mainly used in the implemetnatation of digital input signals to obtain the digital output signals.

Analysis of Linear Discrete System

One of the property that we have learned till now is the linearity of z transform and this property is also used in the analysis process of linear discrete system. The are the system that takes the discrete system as input and after different operations, it also restun us the discrete signals again. Z transform is used to maintain the stability of the result throughout the system.

Frequency Response

We all know that the z transform is used to obtain the result in the z plane. It converts the signal with the time domain into other formats, such as the frequency domain. Therefore, while working with the signals, the z transform is used in finding the frequency response. 

Telecommunication

In the field of telecommunication, all systems are based upon the transfer of a number of bits from one place to another. Z transform is used there to stabilize the flow of the bits as they are in the form of discrete signals. Other techniques are also useful for the same purpose, but while using the z transform, it becomes easy to predict the results and the time at which the communication will occur. 

Feedback Control Problems

A Z transform is used to overcome the feedback control problems of the system. It is done by using different types of signals, including continuous time and discrete time signals. This transform can be used differently when practically implemented.

Identification of the Signals

In operations where experts want to know the exponentially changing values of the signals, they prefer to work with the z transform according to the nature of the signal.

Usage of complex number z in z transform

As we have learned previously, there is a z value that is used in the work of z transform. This is an important feature of the z transform because of its complex nature. It is used to perform complex calculations easily, which were not possible with the Laplace transform.

Signal Processing

Z transform is widely used in signal processing ( as we are reading it from the start). Basically, it is a signal processing tool that is efficiently used in the analysis and interaction of different signals. The poles and zeros used in this type of transform help to recognize the nature of the signal; that is, is it casual, stable, or inverse in nature?

It was a long article based upon interesting facts about the z transform. We were having the discussion of the z transform from our previous session where we saw the basics of the z transform. We saw the properties of the z transform and discussed the important points to clarify our concepts. We also use MATLAB for the implementation of a difference equation. In the end, we learned the simple description of the z transforms application to make our minds about the importance of this topic. If you want to learn more, you can find examples of each property and Use them as your homework. The next lecture is also going to be a little bit complex yet interesting because we are going to learn another transform, which is the Fourier transform.