
Hello friends, I hope you are all doing well. In this article, we can talk about the precision and accuracy of the measurement. Both of these are used to analyze errors in the measurements which can be calculated. In the era of science and modern technology, accuracy and precision are essential to depict the quality of the measurements. To measure the error in the measurement precision and accuracy techniques can be used because both are used for comprehensive measurement analysis.
To calculate or describe the random errors precision of measurement can be used but if we want to describe the systematic error, accuracy of measurements can be used. Now the details of precision and accuracy, their definition, differences, examples, and their application in different fields are given below:

Difference between precision and accuracy:
The main differences between precision and accuracy are given below:

| Precision | Accuracy |
Definition: The reproducibility which can be measured in the measurement is known as precision. On the other hand, precision can also be defined as the set of repeatability measurements and all measurements are close to each other but we precise the closest value. Because highly precise measurements can convey the best and very similar results. |
Definition: The value that we can measure is close to the true value of the measurement is known as accuracy. Another definition of accuracy is that the value that can be measured is approximately equal or close to the accepted and the true value of the measured object. Because accuracy provides the correct measurement of the object which can we measured. If the measurement that we can calculate is close to the standard value of measurement then it can be an accurate measured value. |
Accurate: The measurements that can be calculated are precise but they can't be accurate because high precision can cause low accuracy. |
Precision: The measurements that we can calculate are accurate but they are not precise because high accuracy affects the precision and causes low precision measurement.
|
Determined: To determine the precision we can calculate the object measurement many times and from a set of measured measurements we can determine the precise measurement value. |
Determined: Accuracy can be determined from a single measurement of an object which can be measured. |
Random error: Random error can affect the precise measurement which we can determine. |
Systematic error: The accuracy of the measurement can be affected by systematic error. |
Accurate: The measurements that we can measure are precise but not correct every time. |
Precision: The measurements that can be measured are accurate but these measurements are not correct anyway. |
Reproducibility: Precision can give a degree of reproducibility. |
Conformity: Accuracy provides the degree of conformity of measurements. |
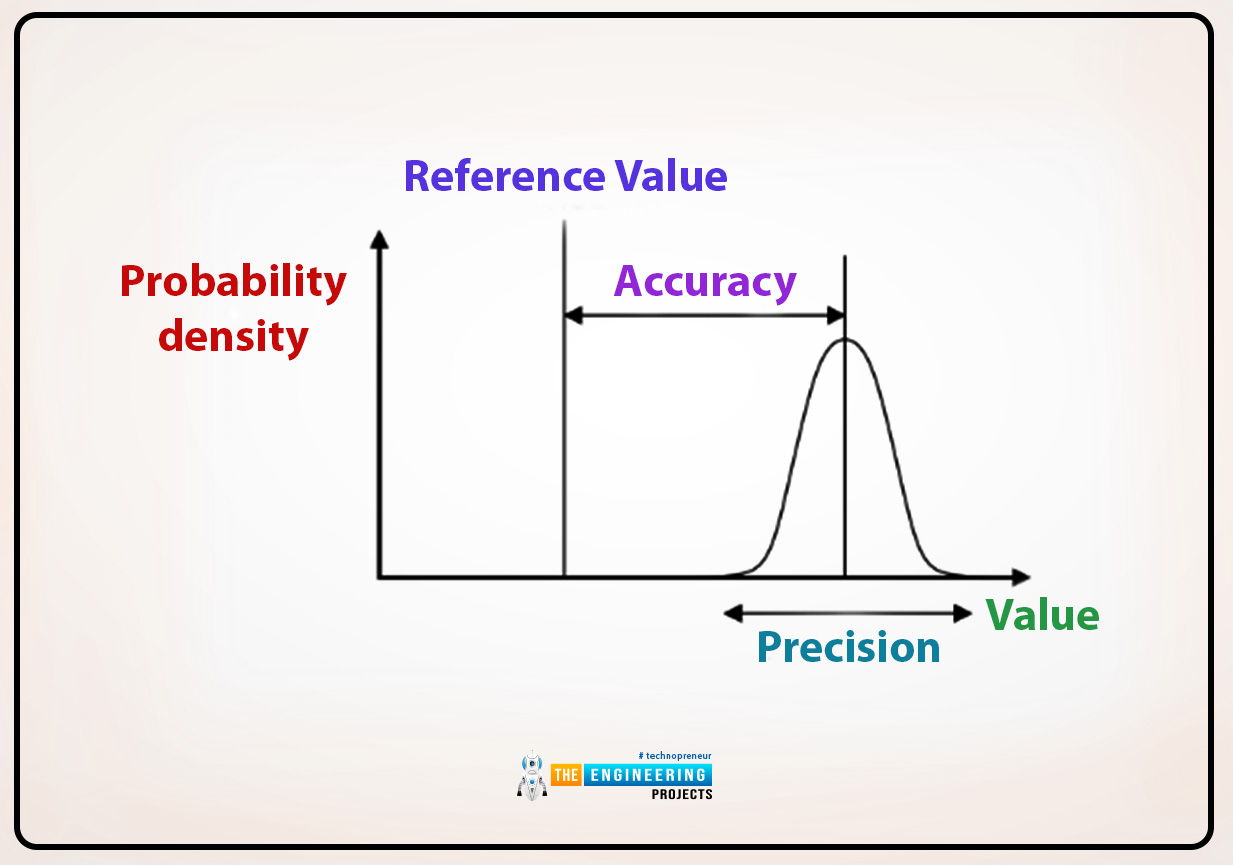
Relationship between the accuracy and precision:
The terms precision and accuracy are different from each other, but somehow they are related to each other. Because when we measure the object or any quantity measurement then it may be accurate but not to be precise but if we determine the periscred measurement then it not to be accurate so that why both terms are not present in the measurements at the same time.to understand the relation and the difference between the accuracy and measurement and to improve the measurement techniques some common points are given there:
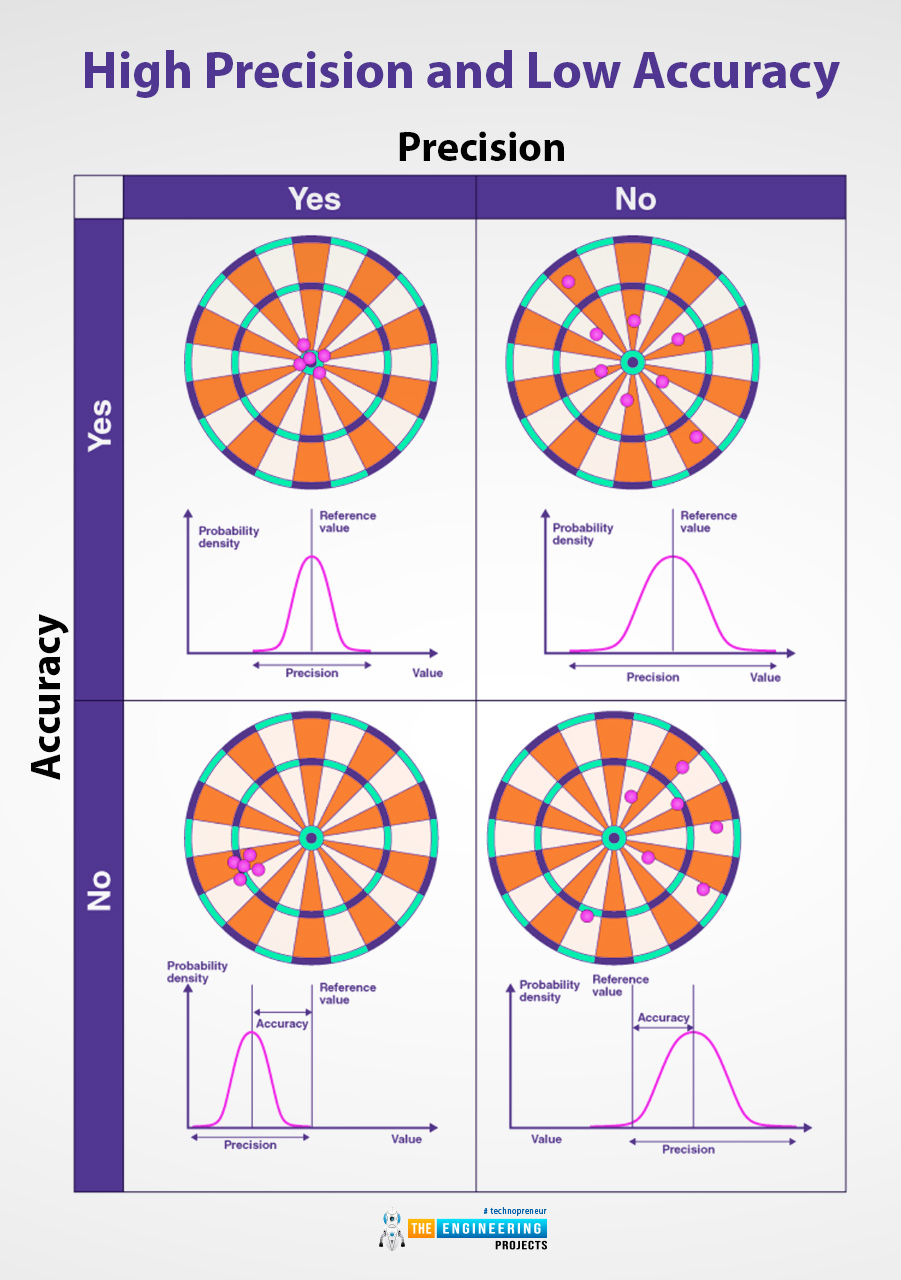
- Low precision and high accuracy
- Low precision and low accuracy
- High precision and high accuracy
- High precision and low accuracy

Low precision and high accuracy:
When the measurements that we can calculate are close to the standard or true value but the measured values are not similar to each other then they have high accuracy but low precision because the measurements are not matched to each other. Some examples are given below:
The measurement of the field which we can calculate is 80 cm, 99.90 cm, and 100.02cm but the true or standard value is 100.10 cm so the values are accurate but they can’t be precise.
If we can calculate the length of an object and the measured value is 70.01m, 80.67m, and 90.01m, the true value is 80.67 then the all values are not precise but they are accurate.
Low precision and low accuracy:
The measured values that can be calculated through measurements are not close to the true value and also the set of measurements are not close to each other all the measurement values are different which means they have low precision and low accuracy. Some examples are given below:
The measurements of the yields are 75.00 cm, 100.00 cm, and 112.00cm but the true value is 120.00cm. These values are not close to each other and neither one value is close to the true value so that is why they have low accuracy and low precision.
For instance, if the measurement is 95.00 cm, 106.00 cm, and 101.00cm but the true value is 105.07cm then they have both low accuracy and low precision.
High precision and high accuracy:
If the measured values that we can measure are close to the true and the standard value and the set of measurements that we can calculate are close to each other then we can say that the measurements which we can be calculated have high accuracy and also have high precision. Some examples of highly accurate and highly precise measurements are given below:
The measurement of the length of the cylinder is 101m, 102m, and 103m and the true or standard value or accuracy is 102m then these values are precise and close to each other and they are also accurate because the measurement is close to the true value.
The measurement of the yield is 80cm, 82cm, 83cm, and 85cm or the true value is 83cm then they have high accuracy and high precision because the values are close to the true value and all sets of measurements are close to each other.
High precision and low accuracy:
The measured measurements are similar or close to each other but these measurements are not close to the true or standard value. some examples of these measurements which have high precision but low accuracy are given below:
- Measurement which we can measure is 79.01, 79.02, 79.03, and 79.08 but the true value is 89.01 That is why the measured values are close to each other but they are not close to the true value so it means they have high precision but low accuracy.
- Another example is if we have measurements 56.8, 56.9, or 60 but the true value is 65.01 these measurements are close to each other but aren't close to the true value so these measurements have high precision but low accuracy.
Quantifying accuracy and precision:
The quantifying of accuracy and precision in detail are given below:
Accuracy:
By using the numerous different statistical measures we can quantify the accuracy. The steps which are involved in quantifying the accuracy are given there:
Root mean squared error
Absolute error
Mean absolute error
Relative error
Their details are given there:
Root mean squared error(RMSE):
When we take the square roots of the average squared errors then it is known as root mean squared error. The formulas which are used for root mean squared error are given below:
RMSE= 1ni=1n(measured valuei-true values)2
Absolute error:
Absolute errors are used to determine the difference between the true value and the measured value. The formulas which are used to determine the absolute error are given below:
Absolute error= measured value- true value
Mean absolute error(MAE):
In the set of measurements to calculate the average error in all the measurements mean absolute error formulas are used. The mean absolute error formula is given there:
MAE= 1ni=1nmeasured value- true value
Relative error:
To express the true value percentage with the absolute error we can use the relative error formula. The relative error formula is given there:
Relative error= (absolute errortrue value) 100
Precision:
By using the measure of variability we can quantify the precision. the steps which are included in the measure of variability are given there:
Coefficient of variation (CV)
Range
Variance
Standard deviation
Details of these points are given below:
Range:
Range is used to measure the difference between the maximum and the minimum values in the set of measured measurement values. The formula which can be used to measure the range is given below:
Range= Maximum value- minimum value
Standard deviation:
By using the mean values from the set of measurements to can measure the dispersion of the measurement set. The formulas which are used in standard deviation are given below:
Standard deviation: 1n-1i=1n(measured value-mean value)2
Variance:
The square root of standard deviation is termed variance. The formula of variance is given there:
Variance= 1n-1i=1n (mmeasured value- mean value)2
Coefficient of variation:
To express the ratio of the standard deviation we can use the formula of coefficient of variation. The formula for the coefficient of variation is given there:
Coefficient of variation: standard deviationmean value 100
Classification of accuracy and precision:
The classification of the accuracy and the precision are given below:
Binary classification:
To measure the statistical measurements we can use accuracy and we can use accuracy in the binary classification to determine or identify the conditions of measurements. By using the accuracy to can determine the exact ratio of the true positive or the true negative.
Types of error that affect the precision and accuracy:
The two main types of errors that affect the precision and accuracy but these two types of error have also types two main types of errors are given below:
Systematic error
Random error
Details of these errors with their types are given there:
Systematic error:
Systematic error is defined as an error that occurs many times due to faulty equipment or may be due to an unskilled person's measurement techniques and many other reasons. But this type of error can directly affect the measurement which can be measured and give the inefficient or bad results of the measurements.
The sources that can cause the systematic error are given below:
Observational errors
Environmental errors
Theoretical errors
Instrumental errors
Observational errors:
Observational errors occur due to human mistakes. When they can read the reading and observe the reading efficiently then observational errors occur some examples are given below:
The reading that can be measured by a human is approximately 3.4cm but it can't observe the certainty and uncertainty within it and also can’t read the exact digits of the reading.
When the unskilled person tries to observe the readings of very small quantities then the observational error occurs maximum because to measure the small quantities skilled person is used to observe the readings.
Environmental errors:
The error occurs due to environmental factors like temperature, humidity, and the fluctuation in the electromagnetic interference and also due to the airflow which can move instruments during the measurements. Some examples of environmental errors are given below:
When we use the thermometer to measure the temperature changing continuously in temperature can cause errors in the measurements.
To measure the current when we used the galvanometer the needle of the galvanometer moved again and again due to the magnetic field these fluctuations can cause errors in the measurements.
Instrumental errors:
The error occurs due to the usage of imperfect or faulty instruments during measurements.
To measure the measurements without error firstly perfect instruments are essential because without this the measurement can't be correct when we measure anything. Some examples of instrumental errors are given below:
To measure the length of an object a ruler can be used but the readings on the ruler are visible clearly because it can be helped to measure the exact length.
A weight machine can be shown the weight of 2kg even if we can't put any object on it this is the instrumental error.
Theoretical error:
Theoretical errors occur when we assume the theory model but nothing can happen in reality according to these models. Theoretical misassumptions can cause different errors in the measurement and provide the un accurate or precise results. Some examples of theoretical errors are given there:
During physics quantities measurements the air resistance is considered negligible.
Random errors:
These errors occur due to various small unpredictable variables and these errors can’t be controlled because they occur in all measurements due to many different small or uncontrolled able variables. Some sources which can cause the random errors are given below:
Environmental variability
Instrumental vartibility
observer variability
Sample variability
Environmental variability:
The fluctuations that can be occurred in the environment at any time like fluctuations in the temperature. Some examples are given there:
The flow of air can distract the measuring instrument from its place and cause errors in the reading
Air currents can also cause errors in the measurements.
Instrumental varaitabity:
The changing that occurs in the instrument during the reading there are many different instruments present that can use the noise or changes in it during measurements. Some examples are given below:
During measuring the current the galvanometer changing the needle again and again can cause errors in the readings or measurements.
Observer variability:
When the numerous observer measured the measurement at the same time their readings were different from each other due to sight issues and many other issues. Some examples are given below:
When the numerous observed reading through the stopwatch and stopwatch couldn't stop at the same time slime gave them vision issues.
Sample variability:
When we can measure the same object but the different samples have changes naturally we can measure them. These natural changes can also cause errors in the measurements. Some examples are given below:
When taking different samples of the same thing or object naturally their width or thickness can be changed then different measurements come with errors.
Improving accuracy and precision:
The accuracy and the precision can be improved if we can follow the following steps which are given there:
For improving accuracy:
Environmental control
Calibration
Instrument maintenance
standardization
For improving precision:
Training
Environmental control
Reptation
Instrument quality
Application of precision and accuracy:
Application of precision and accuracy in different fields are given below:
Scientific research
In modern technology and sciences
In measurements
Healthcare fields
Monitoring environment
In mathematics calculations.
Conclusion:
Precision and accuracy both play vital roles in measurements because in modern physics scientists can measure very small quantities and these quantities of measurement can be accurate without error due to the accuracy and precision. Both terms are the fundamental p[art of measurement in the analysis of comprehensive measurement.
Precise and accurate measurements provide the quality of the measurements because without these terms in measurements, too many errors occur and they are not precise and accurate.



