Hi friends, I hope you are all well and doing good in your fields. Today we can discuss the vector quantities and how we can add the vector by rectangular components. Generally, there are two quantities one is scalar quantities and the other is vector quantity. Scalar quantities are those quantities that have only magnitude but vector quantities are those that can describe both magnitude and direction. So in physics or for complex quantities vectors are used because they can describe both magnitudes with direction.
Vectors can play a very fundamental role in the different fields of physics and mathematics because they can provide accurate and precise measurements. In rectangular components, we can add two or more vectors by breaking them according to their planes. The most efficient method for adding the vectors is adding vectors in rectangular components. Now in this article, we can start our detailed discussion about the vectors and their addition by the method of the rectangular component.
What are vectors?
Vectors can be defined as quantities that can describe both magnitude and direction but they can't provide a description about the position of a quantity. Vectors can be used to describe complex physical quantities like velocity, displacement, and acceleration. Vectors can also used to express the mathematical form of laws and in geometry firstly vectors are used. Some more examples of the vector quantities are given there.

Vectors which may be two or more two can be added by rectangular component because they are the cartesian coordinate system. now the main point about what are rectangular components and their mathematical expression are given there.
What are rectangular components?
In the graph or two-dimensional cartesian coordinate plane, there are axsis which are usually x and y these axsis are known as rectangular components for vectors. But if the cartesian coordinate plane is three-dimensional then the three planes and components are x, y, and z.
For example, if we have the vector A then their components on the two-dimensional cartesian plane are Ax and Ay. But if we have the vector B on the three-dimensional plane then their rectangular components are Bx, By and Bz
Notation:
A: represent vector A
Ax : represent the component of a vector A along with the x-axis
Ay : represent the component of a vector A along with the y-axis
And if they are three-dimensional then,
Az: it can represent the vector A along with the z-axis in the three-dimensional cartesian plane.
i, j and k : these are the unit vectors that can be used according to their rectangular components like i the unit vector of x- the x-axis rectangular component, j the unit vector of the y-axis of the rectangular component, and the unit vector k for the z-axis.
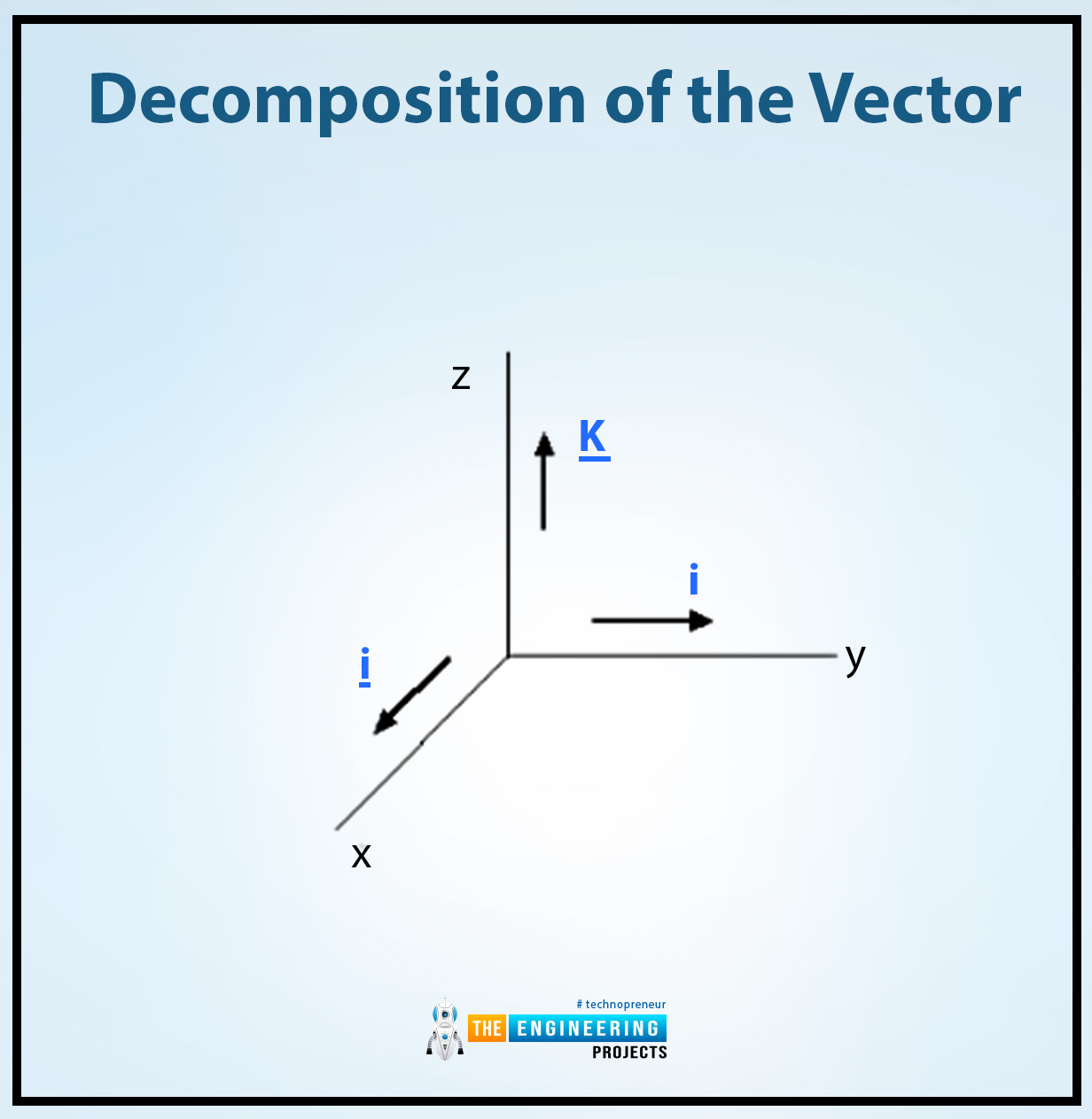
Decomposition of the vector:
Now we know about the rectangular components but if we want to add the vectors by using the rectangular component first we can decompose the vectors according to their component.
Two-dimensional decomposition:
In a dimensional cartesian plane, there are two components x and y so that is why the vector A has the magnitude A and also has the angle 𝚹 on the x-axis. Their decomposition equation is given there:
A = Axi + Ayj
Where,
Axi: A cos𝚹
Ayj : A sin𝚹
Three-dimensional decomposition:
In three three-dimensional cartesian planes the x, y, and z are the components for the vector A then there decomposition of rectangular components can be written as:
A = Axi + Ayj + Azk
Vector addition by rectangular component:
Vector addition by rectangular component is also known as the Analytic method of vector addition. This method can add the vectors efficiently and the chances of error are very low as compared to other methods like the head-to-tail rule or other graphical methods. Now we can start the vector addition by rectangular components.
Let's imagine we have two vectors one vector A or the other is a vector B now we can add them to the rectangular cartesian coordinate system and suppose their resultant is R and these vectors make an angle θ on the x-axis. By using the head-to-tail rule the resultant of two vectors which is A or B are R = A + B now we can resolve the vectors A, B and the resultant vector R into their rectangular components.
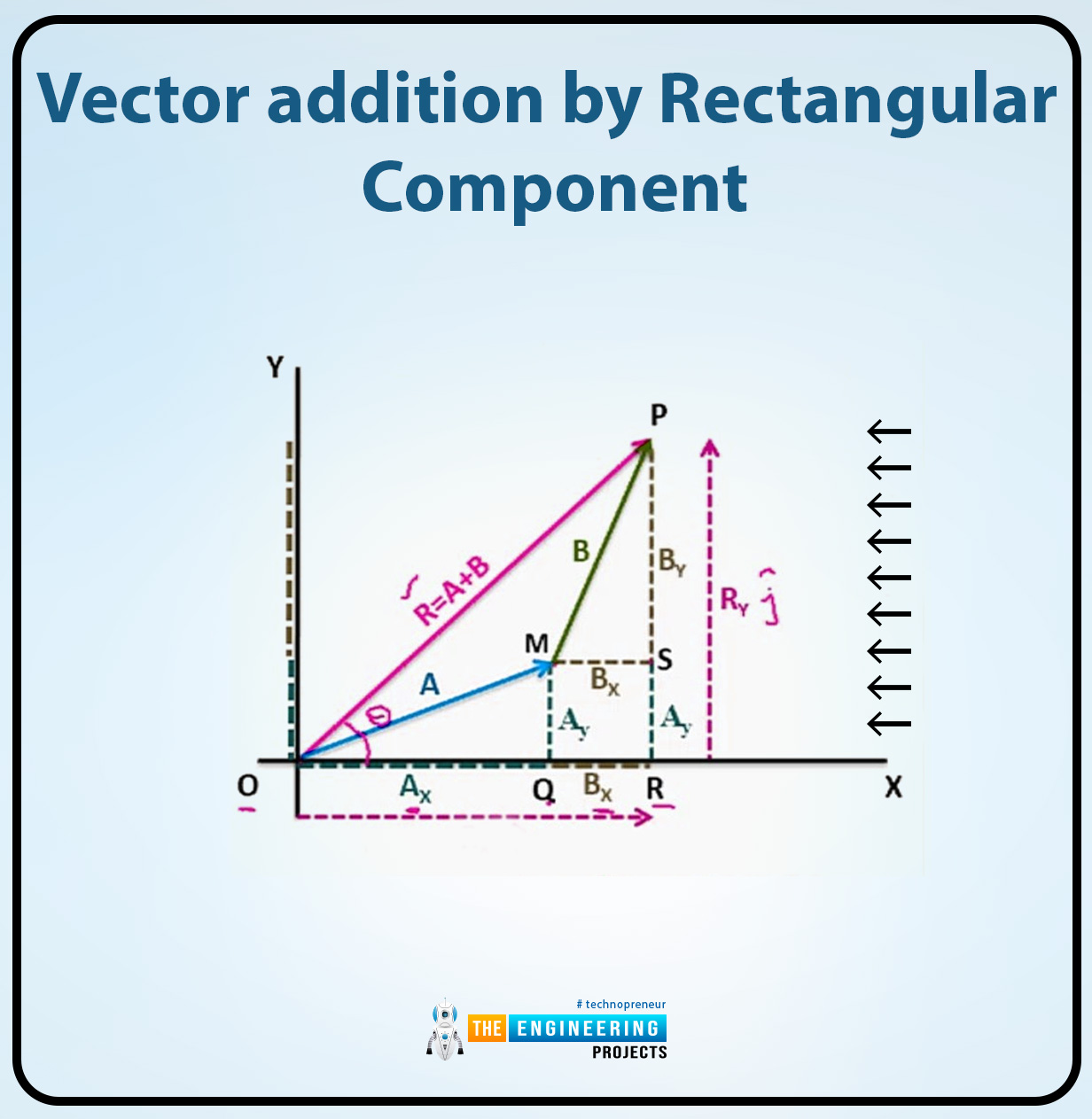
Now in this figure, the vector addition is shown and the rectangular components of the vector A, B and the resultant vector R are also shown now we can start our derivation to resolve the all vectors in the figure.
Firstly we can find the x component of the resultant and the y component of the resultant.
Resultant of the x components:
As shown in the figure,
- OQ is the magnitude of the vector A on the x component.
And,
- MS is the magnitude of the vector B on the x component.
then,
- OR is the magnitude of the resultant vector R on the x component all are shown in the given figure.
Then according to the given figure, we can write these magnitudes of the vector as:
OR = OQ + QR
Since the QR is also equal to the MS. we can write it as,
OR = OQ + MS
And according to the vectors it can be written as:
Rx = Ax + Bx ……………. (i) equation
The sum of the magnitude of the vector A and the vector B on the x component is equal to the magnitude of the resultant vector R on the x component which can be shown in the (i)equation.
Resultant of the y components:
As shown in the figure,
- QM is the magnitude of the vector A on the y component.
and,
- SP is the magnitude of the vector B on the y component.
then,
RP is the magnitude of the resultant vector R on the y component which is shown in the figure.
Then according to the given figure, we can write these magnitudes of the vector as:
RP = RS + SP
According to the given figure the RS is also equal to the QM so we can also write the equation as;
RP = QM + SP
Now this equation can be written according to the vectors as:
Ry = Ay + By ………… (ii) equation
The sum of the magnitude of the vector A and the vector B on the y component is equal to the magnitude of the resultant vector R on the y component which can be shown in the (ii)equation.
Unit vector:
Now we can write the resultant vector on the x component or y component with their unit vectors.
The resultant vector of the x component with its unit vector is written as Rx i.
The resultant vector of the y component with its unit vector is written as Ryj.
Then the resultant vector with its unit vector in the equation can be written as:
R = Rxi + Ryj
Addition of the x component and y component resultant:
Now we can put the values of Rxi or Ryj in the resultant vector R.
R = Rxi + Ryj
Putting the values from the equation (i) and equation (ii) and written as
R = ( Ax + Bx) i + ( Ay + By ) j
This equation is used to add the vectors on the rectangular components.
The magnitudes of the resultant vector R:
After adding the vectors on the rectangular component we can also find their magnitude by using some formula. The formula which we can use to find the magnitude of the resultant
R is given there:
R = Rx2 + Ry2
And if we want to find the magnitude of the vector A and vector B we can put the values of the resultant vector Rx and the resultant vector Ry in the given formula and we can write this formula as:
R = (Ax+Bx )2+ (Ay+By)2
This formula can be used to find the magnitude of the vectors that can be added to the rectangular component.
But if we can find the magnitude of the resultant R which has the vectors A and vector B then we can also use this formula which is given there :
R = A2 + B2 + 2ABcosӨ
Special cases:
There are some special cases in which the value of θ can be different so we can change some formulas. Some special cases are given there:
If the value of θ = 90° then,
R = A2 + B2
But if the value of θ= 0° then,
Rmax = A + B
And if the value of θ=180° then,
Rmax = A – B
Resultant vector R direction:
Vectors can describe the magnitude but they can also describe the direction so after finding the magnitude we can also find their direction by using the formula. To find the direction of the resultant vector R we can use the formula which is given below:
tanθ = RyRx
Also, it can be written as:
θ = tan-1 RyRx
But if we want to find the direction of the vectors A and B we can put the values of Rx and Ry. and it can be written as:
θ = tan-1 AY+ByAx+Bx
These all formulas can be used for two-dimensional vectors but if we want to find the three-dimensional vector or many other vectors we can use the other formulas that are given there.
Two vectors in three dimensions of rectangular component:
The two vectors A and the vector B can lie in the three dimensions in the rectangular cartesian coordinate system.
Components of resultant vectors in three dimensions:
The components of the resultant vectors in three dimensions are given there:
Rx components on the x-axis: Ax, Bx
Ry components on the y-axis: Ay, By
Rz components on the z-axis: Az, Bz
Components of vectors in three dimensions:
The components of vectors A and B in the three dimensions are given there:
A = Axi + Ayj + Azk
B= Bxi + Byj + Bzk
The sum of these vectors in three dimensions:
A sum of these two vectors in the three dimensions is given there:
R = Rxi + Ryj + Rzk
Then put the values and get the equation which is given there:
R = (Ax+Bx) i + (Ay+ By) j + (Az+ Bz) k
This formula is used for the two vectors on the three dimensions.
Multiple vectors in two dimensions:
We can also add the multiple vectors in the two dimensions. Then the resultant components on the x, y, and z axes with their vector components are given there:
For the vectors A1, A2 and the vector An.
then,
R = i=1n Ai
Rx = i=1nAix
Ry= i=1nAiy
Magnitude formula for the three dimension resultant vector:
The formula that can be used for resultant vectors in these three dimensions is given there:
R = Rx2 + Ry2 + Rz2
Magnitude for the coplanar vectors:
To find the magnitude of the coplanar vectors A, B, C, D and ........ we can use the formula which is given there:
R = (Ax+Bx+Cx +...........)2+ (Ay+By+Cy+..........)2
The direction of the coplanar vector:
To find the direction of the coplanar vector we can use this formula which is given there:
θ = tan-1Ay+By+Cy..........Ay+BY+Cy+...........
Determination of the angle θ of the resultant vector R in its rectangular components:
Determination of θ:
By using the given formula we can first determine and find the θ.
θ= tan-1RyRx
After the determination of the angle check the signs of Rx and the Ry in the rectangular cartesian coordinate system and determine their resultant quadrant according to their signs.
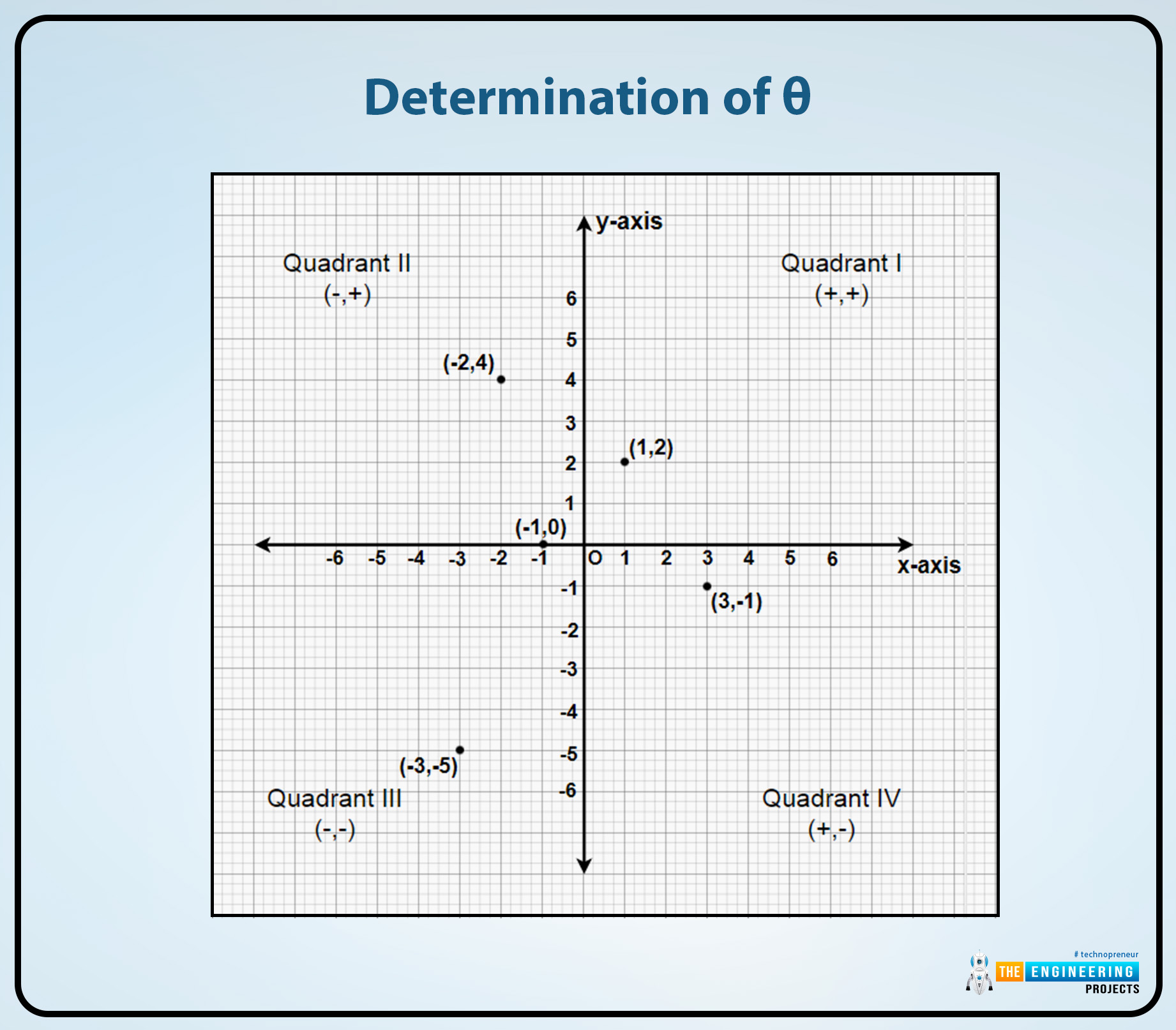
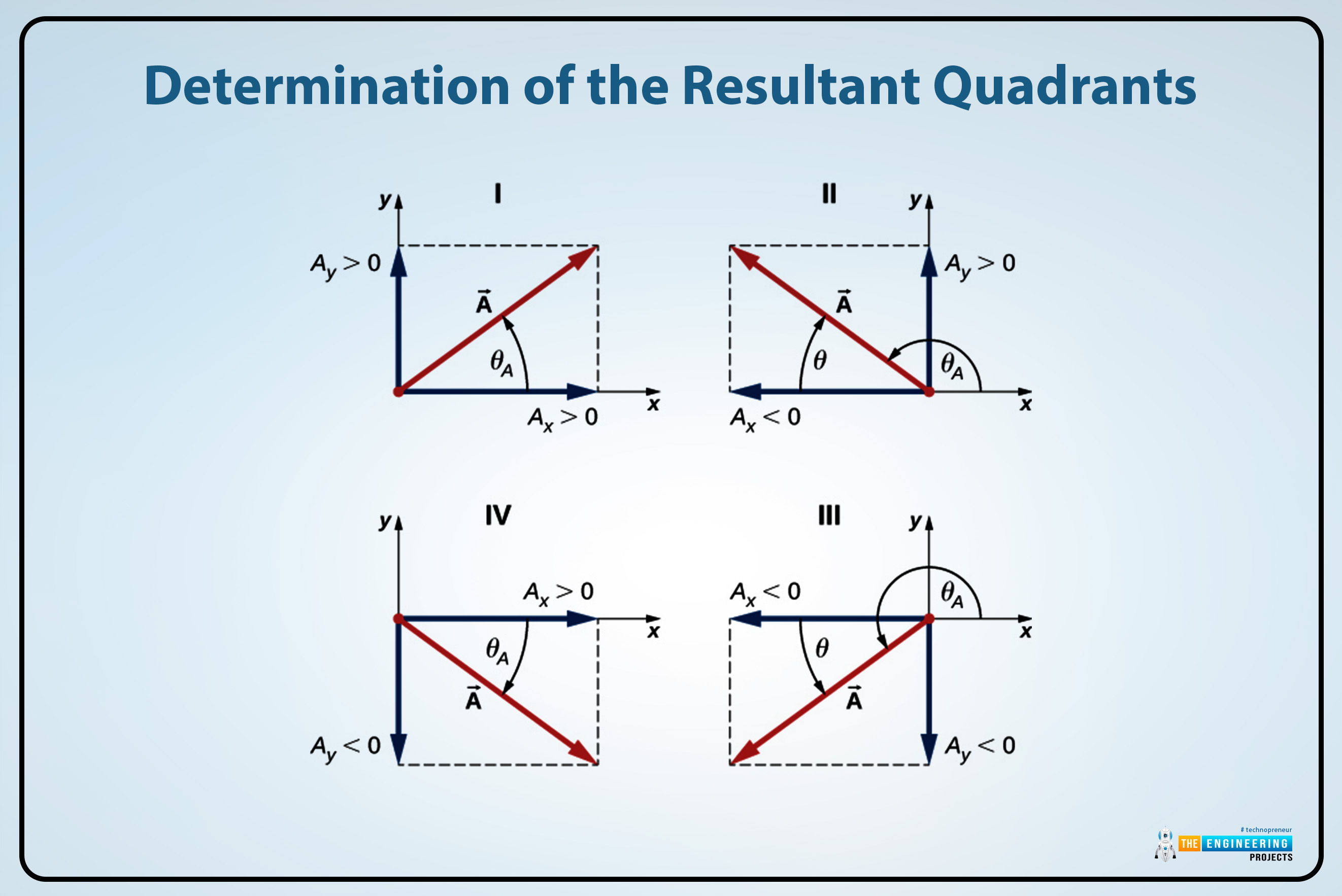
Determination of the resultant quadrants:
Determine the resultant quadrant through the signs of Rx and the Ry. The rules which can be followed to determine their quadrants are given there:

1st quadrant:
The resultant vector R lies in the first quadrant if the sign is positive for both of them Rxand the Ry vectors. Their direction is
θ = Φ
2nd quadrant:
The resultant vector R lies in the second quadrant if the Rx is negative and the other vector Ry is positive. And their direction is,
θ = 180° – Φ
3rd quadrant:
The resultant vector R lies in the third quadrant if the Rx and the Ry both are negative no one from them is positive. Their direct is,
θ = 180° + Φ
4th quadrant:
The resultant vector R lies in the fourth quadrant if the Rx is positive and the other resultant vector Ry is negative. Their direction is,
θ = 360° – Φ
Summary:
For adding the vectors in the rectangular components in a very efficient way we can use some rules. These rules are as given below:
Vectors: First we can determine the x and y components for all vectors in two dimensions and if they are three-dimensional addition then also find the z components of all vectors.
Resultant vector Rx: then to find the resultant vector Rx which is the x component, add all the vector components on the x axes.
Resultant vector Ry: then to find the resultant vector Ry which is the y component, add all the vector components on the y axes.
Magnitude: After this, we can find the magnitude of resultant vectors by using the given formula:
R = Rx2 + Ry2
Direction: then we can also find the direction of the vector along with the magnitude by using the given formula:
θ= tan-1RyRx
Examples:
Some examples of adding the vector in a 2D or 3D rectangular system are given there:
Adding the vectors in 2D:
The given vectors are A and vector B.
The values of these vectors are:
A= 6i + 4j
B = -4i + 3j
Then add by using the resultant formula R = A + B
Then find Rxand Ry and add them,
Rx= 6 + (- 4) = 2
Ry = 4 + 3 = 7
Then,
R = 2i + 7j
Magnitude:
R= Rx2+ Ry2
By putting values,
R = 22+ 72
R= 4+ 49
R= 53
R≈ 7.280
Direction:
After finding the magnitude we can find direction by using the given formula:
θ = tan-1RyRx
By putting the values we get,
θ = tan-172
θ ≈ 16.35
Now add the three vectors in 3D:
The given vectors are A vector B and the vector C.
The values of these vectors are given there;
A= 6i + 4j + 1k
B = -4i + 3j + 5k
C = -1i + 3j + 2k
Then add by using the resultant formula R = A + B + C
Then find Rxand Ry and Rz and then add them,
Rx=6+ (- 4) +(-1) = 1
Ry=4 + 3 + 3 = 10
Rz= 1 + 5 +2 =8
Then,
R = 1i + 10j +8k
Magnitude:
R= Rx2+ Ry2+Rz2
By putting values we get,
R = 12+ 102 + 82
R= 1 + 100+ 64
R= 165
R ≈ 12.85
Practical applications:
The addition of the vectors in the rectangular components can be used in different fields of physics because it is an analytic method and provides precise and accurate calculations so scientists in physics or mathematics use this method for the calculation of complex physical quantities. Now we can discuss some applications of adding vectors by rectangular components in some different fields.
Robotics:
To determine for find the orientation and position of the robot's arms or legs in an efficient way we can use the vector addition or analytic method because it can provide accurate information without any possible errors.to achieve coordination and control of the robots we can also use the vector addition method by decomposing their component according to the axis.
Physics and engineering:
For the analysis of the vector quantities like velocity, displacement, acceleration, and force in the accurate or precise method we can use the analytic or the vector addition by rectangular component method. In navigation, if we want to calculate the resultant velocity we can use this analytic method by adding the vectors which are the velocity of the wind and the velocity of the aircraft from which they can fly. This, there are many examples in which this method can be used for calculating the quantities. For example, many external forces can act on the body then we can all add them by using this analytic method and get the sum of all external forces which can act on them.
Computer graphics:
In the field of computer graphics, we can transform the objects their position, and movements, and we can calculate all of these movements through vector addition or analytic methods. The complex motion of the objects their movement, position, and all control on them was handled efficiently through breaking down their components according to their rectangular components axes.
Applications of vector addition in the advanced topics:
With time or in the modern era of science and technology vector addition can be used in many new different fields some are given there:
Spherical coordinates:
The vector A in the spherical coordinates their magnitude can be represented through the A and the angle between them is represented through θ and also represented through the azimuthal angle Φ. In spherical coordinates the vector addition or analytic method can also be used to decompose the components, adding them or also convert them into their original form.
Vector addition in different coordinate systems:
Vectors can be added basically or generally into the rectangular or cartesian coordinate system but vectors can also be added in many different coordinate systems like polar, polygram, cylindrical, or in many different spherical coordinate planes. But in different spherical coordinate systems, we can follow many other different rules which may be addition or different from the addition of vectors in the rectangular coordinate system.
Polar coordinates:
The vector A in the polar coordinate system, their magnitude can be represented through A and the angle can be expressed through θ. But the addition in the polar coordinate system is difficult so that's why if we want to add the vector in the polar coordinate system we can convert them, decompose them, and then add them into the rectangular component and if the need arises we can convert them and then added them.
Common mistakes and the challenges in the vector addition by its rectangular components:
In vector addition in its rectangular components, some mistakes can occur when the vectors are complex and the calculation becomes challenging. Some common mistakes and challenges are given there:
Neglecting units:
In the vector addition or during the calculations units can play an essential role but if we can neglect them and can't track them properly then the inaccurate calculation or result from chances increases if we can track the units properly then there is no chance for error and the result are accurate and efficient. Mixing up of units can also provide inaccurate or false results.
Misalignment of coordinate axes:
When we add these vectors to the cartesian or any coordinate system it is essential to check their coordinates and components properly because if any vector lies on the wrong coordinate plane the result is incorrect. Coordinate planes can play a very essential role in a vector addition misleading coordinate axes always provide inaccurate calculations and results.
Incorrect component calculations:
When we can perform the trigonometric functions the chances of error are possible but if we can check the calculations again and again then there is no chance of error. If the signs and values of vectors according to their components are not correct then their calculation results are also inaccurate. Because they can cause different significant errors so that's why double double-checking the units and the components in the coordinate plane is essential for precise and efficient results.
Conclusions:
In different fields of physics or mathematics or many others like engineering, robotics, and computer graphics vector addition can play a very essential and powerful role also vector addition can be handled and provide control on different types of robots. Vector addition can also play an essential role in understanding complex vector quantities and also help to understand the theory of trigonometrics and resolve complex trigonometric problems in a very efficient way.



