Hi, friends I hope you are all well and doing the best in your fields. Today we will discuss the cross or the vector product. In the previous article, we discussed vector quantities, scalar quantities, and the scalar or dot product with their properties, and applications in different fields of science now we can talk about the cross or vector quantities in detail because vectors are used in mathematics, physics, engineering or many other fields. Algebraic operations can also be solved by using the vectors. Vectors are widely used because they can provide the magnitude and direction of a quantity.
The vector product is also known or termed as the cross product. Vector product or in the cross-product are binary vectors or these vectors are perpendicular to each other in the three-dimensional plane. Generally, the cross or the vector product can solve complex algebraic operations like torque, magnetic force, and angular momentum. The mathematics which is the field of science, the cross or the vector product can usually represent the product of the given area with the direction where the two vectors are placed in the Euclidean space or the three-dimensional Cartesian plane. The scalar or the dot product can be represented by the sign or symbol () but the cross or the vector product can be represented by the symbol which is termed a cross. The scalar or the dot product is different from the cross or the vector product because the scalar product can be also termed or used for calculating the projection between two vectors. But the vector or cross product is used for the two perpendicular vectors calculation. Now we can start our deep discussion about the cross or the dot product, algebraic operations, applications, and examples.
History:
In the late 18th century, the Quaternion algebraic operation and the first products of the vectors which are violets the commutative law can be described by the scientist William Rowan Hamilton. The experiment can be performed by William in which he can do the product of two vectors and these are the quaternions and the other part for the product is zero which is scalar then their results also contain the vector or the scalar part. The part of scalar and the vector in the result of William product expressed the cross product of the two vectors which can be represented by the A B and the dot product of the two vectors can be expressed as the A B.
After this, the scientist Josiah Willard Gibbs in the 18th century 1881, with Oliver Heaviside represented the expression that can be used for the dot products of the two vectors and also for the cross product of the two vectors which are given there:
The dot product can be expressed through and written as;
A B
The cross product of the two vectors can be expressed through the cross and written as:
A B
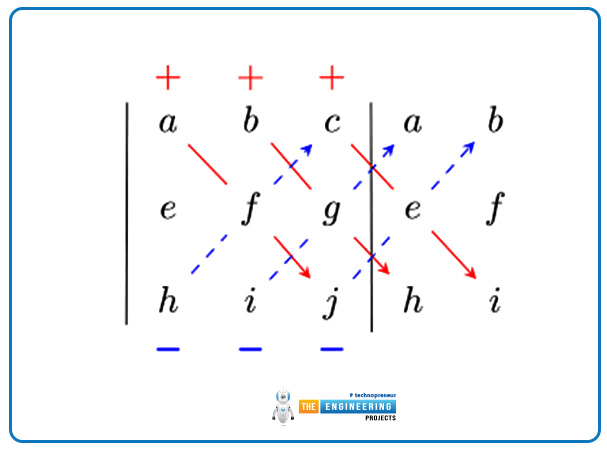
As we can see the expression for both the dot and the cross product expressed that the vector A can be multiplied by the vector B and they can’t violet the commutative law so that's why their matrix can be always 3 3 and it can also be explained by the scientist, Saru's and their law or rule can be termed as Sarrus rule which is given there:
Definition:
Cross or the vector product can be defined as:
“when the product of the two vectors is the vector quantity it can be represented as A B then it is teremed as the vector product or also the cross product. And the resultant vector which can be denoted by the C are perpendicular to the both of the vector A and the vector B.”
Mathematical expression:
Mathematically the cross or the vector product can be written as:
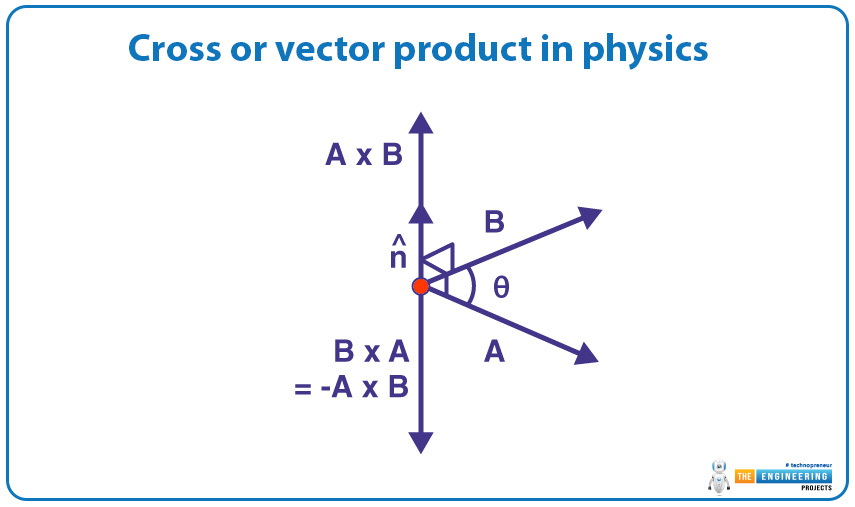
A B = AB sinθ n
There,
A represented the vector A
B represented the vector B
And,
A represents the magnitude of the vector A
B represented the magnitude of the vector B
The θ represented the angle between the vector A and the vector B which lies in the 0° to 180°. And the unit vector which is perpendicular to the vector A and the vector B can be denoted through n.
The product of the two vectors, vector A and vector B is zero (0) when both of these vectors A and vector B are parallel to each other.
The magnitude and the direction of the cross or the vector product:
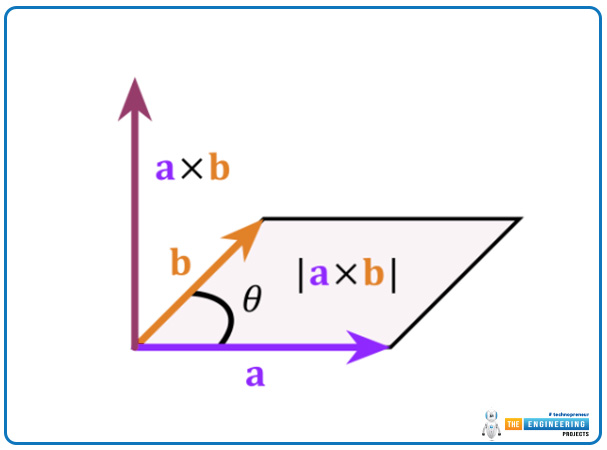
The magnitude and the direction of the vectors can be represented through the right-hand rule. In which the direction can be shown in the right-hand rule and the magnitude of two vector products is always equal to the parallelogram which is given or in which the vector product can be done.
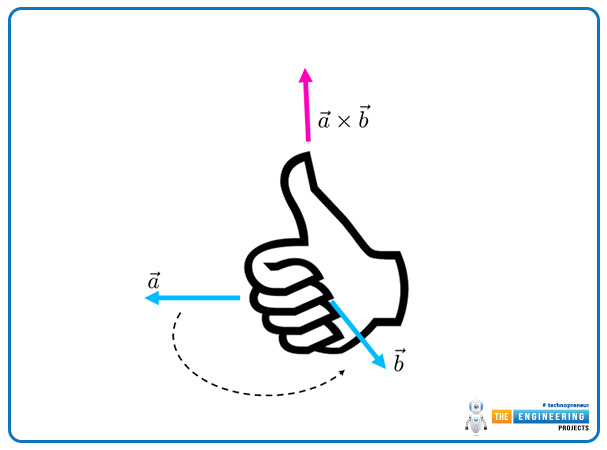
What is the right-hand rule in the term of cross or vector product?
The right-hand rule in the term of the cross or the vector product can be defined as:
"The thumb of the right hand determines the direction of the resultant vector C which is the product of two vectors cross product and when we can curl our finger in the direction of the thumb it indicates the direction the vector A and after proper curling of fingers, it indicates the direction of the vector B."
Direction of the cross or vector product:
As we discuss the right-hand rule in terms of the cross or dot product the thumb and the curling finger represent the directions of the vector and also the direction of the resultant vector through the thumb.
In the given figure the cross or vector product of two vectors can be shown. The thumb represents the resultant vector which is equal to the product of two vectors A and the vector B
The fingers and the curl fingers can represent the direction of both vector's magnitude and the θ represents the angle between both of these vectors in the area of a parallelogram.
Mathematical calculation or notation:
The product of the two vectors with their units vector, coordinate equation, or the mathematical expression are given there:
Coordinate equation or formula for the cross or vector product:
Let's suppose the two vectors, the vector A and the vector B which is equal to the,
A = A1 i + A2j + A3k
B = B1 i + B2j + B3k
As we know i , j and k are the unit vectors that can be oriented in the orthonormal basis positively and they can be written as:
k i = j
j k = i
i j = k
Now according to the anti-commutativity law, or when these unit vectors can be oriented negatively then the orthonormal basis can be written as:
i k = – j
j i = – k
k j = – i
Now when we can do the product of the two vectors, vector A and vector B with their unit vector which can follow the distributive law then it can be written as:
A = A1 i + A2j + A3k
B = B1 i + B2j + B3k
And
A B = (A1 i + A2j + A3k) (B1 i + B2j + B3k)
Then,
A B = A1 B1 ( i i ) + A1 B2 ( i j ) + A1 B3 ( i k ) + A2B1 ( j i ) + A2B2 ( j j ) + A2B3 ( j + k ) + A3B1 ( k i ) + A3B2 ( k j ) + A3B3 ( k k) …… (i) equation
We also know that:
i i = j j = k k = 0
Because the vectors are perpendicular and they can't follow the law of the commutative.
By putting the values of the unit vectors in the equation (i)
A B = A1 B1 (0) + A1 B2 (k) – A1 B3 ( j) – A2B1 ( k ) + A2B2(0) +A2B3 (i) + A3B1 ( j) – A3B2 (i) + A3B3 (0)
Then arrange them and then it can be written as;
A B = A2B3 (i) – A3B2 (i) – A1 B3 ( j) + A3B1 ( j) + A1 B2 (k ) – A2B1 ( k )
Now we take common the same unit vectors i, j, and k and write as,
A B = ( A2B3 – A3B2) i + ( A3B1 – A1 B3) j + ( A1 B2– A2B1 ) k
The products of the two vectors, vector A and vector B are the component of the scalar and their resultant vector are C which are equal and written as:
C = C1i + C2j + C3k
So that's why the resultant vectors with their unit vector are equal and written as:
C1i = A2B3 – A3B2
C2j = A3B1 – A1 B3
C3k = A1 B2– A2B1
Also, it can be written in the matrix, column matrix which is given there,
C1i C2j C3k |
A2B3 – A3B2 A3B1 – A1 B3 A1 B2– A2B1 |
=
Matrix:
To represent the vector products the determinants can be used and they can be written as:
i A1 B1 |
j A2 B2 |
k A3 B3 |
A B =
But if we can use the Sarrus rule in the matrix then it can be written as:
A B =( A2B3 (i) + A3B1 j + A1 B2k ) – ( A3B2 i + A1 B3 j + A2B1 k )
Then it can also be written as:
A B = ( A2B3 – A3B2) i + ( A3B1 – A1 B3) j + ( A1 B2– A2B1 ) k
And these are the components of the cross or the vector products.
Characteristics and properties of the cross or the vector product:
The characteristics and the main properties of the cross or the scalar product are given there:
Area of a parallelogram
Perpendicular vectors
Self vector product
Violation of the commutative law
Parallel vectors
Anti parallel vectors
Vector product in the rectangular component
Distributivity
Scalar multiplication
Orthogonality
Zero vector
Their detail is given there:
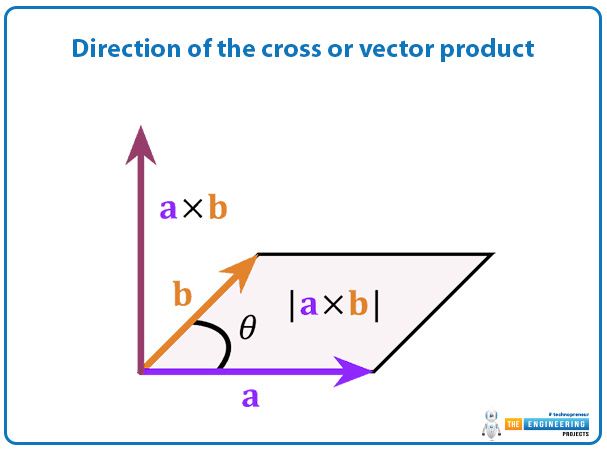
Area of a parallelogram:
The product of the two vector quantities, the magnitude of these vector A and vector B is equal to the area of a parallelogram along with their sides. The area of the parallelogram is equal to,
Area of a parllelogram= length height
Area of the parallelogram = ( A) (B sinθ)
there,
A represents the length
B represents the height
sinθ represents the angle between vector A and vector B
The total area of the parallelogram with their sides is the magnitude of these vector products. and it can be written as:
Area of a parallelogram = ( A B magniytude)
Also written as:
Area of a parallelogram = A B
Pre[endicular vectors:
When the two vectors, vector A and vector B are perpendicular to each other then their magnitude is always maximum because the angle θ between them is equal to 90°, then it can be written as:
A B = AB sin 90° n
As we know that:
sin 90° = 0
Then,
A B = AB (1) n
A B = AB n
And it is the maximum magnitude of the two vectors in the cross or vector product. But in the case of their unit vectors, it can also be written as:
k i = j
j k = i
i j = k
It can also be written as:
i k = – j
j i = – k
k j = – i
Self-vector product or zero vector:
When the vector can do self product then its result is always equal to the zero and it can also be known as zero or maybe it termed as the null vector. The mathematical expression for self-vector products is given there:
A A = AA sin 0° n
A A = 0° n
A A = 0 this is the zero or the null vector. Another example for the vector B is given there:
B B = BB sin 0° n
B B = 0° n
Then,
B B = 0
Unit vectors:
For the unit vectors, the self-product is also equal to the null or zero vector and written as:
i i = ii sin 0° n
i i = (1) (1) sin0° n
i i = 0° n
i i = 0
So the other unit vector self-product is also equal to the null or zero vector and can be written as:
j j = 0
k k = 0
And
i i = j j = k k
Violation of commutative law or anti-commutativity:
The cross or the vector product of the two vectors, vector A and the vector B are not to be commutative because they can't follow this law because the vectors are perpendicular to each other.
Let the vector A and the vector B and the sin θ be the angle that is present between the product of these two vectors and it can be written as:
A B = AB sinθ n ……… (i) equation
And if we can reverse them and write them as:
B A = BA sinθ(- n )
And also it can be written as;
B A = AB sinθ(- n ) ……… (ii) equation
According to the commutative law
AB = BA
Now compare the equation (i) and the (ii) equation
A B = – B A
A B ≠ – B A
Thus, it can proved that the cross or the vector product of the two vectors A and b can't follow the commutative property.
Parallel vectors:
When the two vectors, vector, and vector B are parallel to each other then always their cross or the vector product is equal to the null or the zero vector.
Mathematical expressions for parallel vectors are given there:
A B = AB sinθ n
In parallel vectors θ = 0° then,
A B = AB sin (0) n
A B = AB (0) n
A B = (0) n
A B = 0
Anti-parallel vectors:
When the two vectors, vector, and vector B are anti-parallel to each other then always their cross or the vector product is equal to the null or the zero vector.
Mathematical expressions for parallel vectors are given there:
A B = AB sinθ n
In parallel vectors θ =180° then,
A B = AB sin (180) n
A B = AB (0) n
A B = (0) n
A B = 0
Vector product in the rectangular component:
The cross or the vector product can be done in the cartesian or the rectangular components and there three components are the scalar but their product result is always the vector quantity.
Let's suppose the two vectors, the vector A and the vector B which is equal to the,
A = A1 i + A2j + A3k
B = B1 i + B2j + B3k
As we know i , j and k are the unit vectors that can be oriented in the orthonormal basis positively and they can be written as:
k i = j
j k = i
i j = k
Now according to the anti-commutativity law, or when these unit vectors can be oriented negatively then the orthonormal basis can be written as:
i k = – j
j i = – k
k j = – i
Now when we can do the product of the two vectors, vector A and vector B with their unit vector which can follow the distributive law then it can be written as:
A = A1 i + A2j + A3k
B = B1 i + B2j + B3k
And
A B = (A1 i + A2j + A3k) (B1 i + B2j + B3k)
Then,
A B = A1 B1 ( i i ) + A1 B2 ( i j ) + A1 B3 ( i k ) + A2B1 ( j i ) + A2B2 ( j j ) + A2B3 ( j + k ) + A3B1 ( k i ) + A3B2 ( k j ) + A3B3 ( k k) …… (i) equation
We also know that:
i i = j j = k k = 0
Because the vectors are perpendicular and they can't follow the law of the commutative.
By putting the values of the unit vectors in the equation (i)
A B = A1 B1 (0) + A1 B2 (k) – A1 B3 ( j) – A2B1 ( k ) + A2B2(0) +A2B3 (i) + A3B1 ( j) – A3B2 (i) + A3B3 (0)
Then arrange them and then it can be written as;
A B = A2B3 (i) – A3B2 (i) – A1 B3 ( j) + A3B1 ( j) + A1 B2 (k ) – A2B1 ( k )
Now we take common the same unit vectors i, j, and k and write as,
A B = ( A2B3 – A3B2) i + ( A3B1 – A1 B3) j + ( A1 B2– A2B1 ) k
The products of the two vectors, vector A and vector B are the component of the scalar and their resultant vector are C which are equal and written as:
C = C1i + C2j + C3k
So that's why the resultant vectors with their unit vector are equal and written as:
C1i = A2B3 – A3B2
C2j = A3B1 – A1 B3
C3k = A1 B2– A2B1
Also, it can be written in the matrix, column matrix which is given there,
C1i C2j C3k |
A2B3 – A3B2 A3B1 – A1 B3 A1 B2– A2B1 |
=
Determinant:
The formula which can be derived from the cross or the vector product can also be written in the form of a determinant and their mathematical expression is given there:
i A1 B1 |
j A2 B2 |
k A3 B3 |
A B =
Distributivity property:
The cross or the vector product of the two vectors follows the distributivity property. Their mathematical expression is given there:
A ( B + C ) = A B + A C
In cross or the vector product this distributivity property can be proved by the vectors.
orthogonality:
The cross or the vector product of the two vectors A and vector B ( A B ) is always orthogonal to the vector A and the vector B.
Scalar multiplication:
The scalar multiplication can also be done with the cross or the vector product of the vectors. Their mathematical expression can be written there:
( cA) B = c ( A B)
c represented the scalar multiplication, A represents the vector A, and B represents the vector B.
Applications of the cross or the vector product:
In the various fields of science, vector or cross products can be used generally but in mathematics, computer graphics, physics, or engineering mostly cross or vector products can be used. Some applications of vector products with details are given there:
Computer graphics
Physics
Engineering
Computer graphics:
In computer graphics, wide cross or vector products can be used in different programs. The major parts in which the cross or the vector products are used are given there:
Rotations: in the graphics where the algorithm can be used the cross or the vector product is widely used. It can also be used to compute the angular velocity and also to determine the axis of the rotation. In animations or the different stimulating systems cross or the vector product can be used to simply them.
Normal vectors: for the lightening in the calculations in the computer graphing program the normal vectors are used generally. The non-parallel vectors which are lying in the programming of the vector or the cross product can be used to simplify them.
Physics:
In physics, the cross or the vector product is widely used to solve complex algebraic operations along with geometry the main fields in which the vector product can be used are given there:
Angular momentum: angular momentum is the product of two different vector quantities, one is linear momentum which is denoted by ρ and the other is position vector which can be denoted by the r . Their formula or mathematical expression is given there:
L = p r
Their L denotes the angular momentum.
Angular momentum can be widely used in dynamic rotation or isolated systems.
Torque: torque is the product of two different vector quantities, one is force which is denoted by F and the other is position vector which can be denoted by the r . Their formula or mathematical expression is given there:
τ = F r
Their τ denotes the torque.
Engineering:
Application of vector products in engineering fields where mainly the cross product are used is given there:
Magnetic force: (B)
Moment of a force:F
Advanced topics in which cross or the vector product can be used:
With time or with the complexity of the quantities or algebraic operations cross or vector products can be used in many different new fields or they can also be improved the advanced topic mainly in which the cross or the dot product can be used are given there:
Vector triple product:
To simplify the complex vector problem or the complex problem in physics the triple product of the vectors can be used because it can simplify them in a very efficient or accurate way. The mathematical expression or the formula that can be used in vector triple product is given there:
A ( B C ) = ( A . C ) B – ( A . B) C
there,
A represented the vector A
B represented the vector B.
C represented the vector C.
Three vectors can be used in this product so that is why it can also be termed as the triple vector product.
Examples:
Angular momentum: angular momentum is the product of two different vector quantities, one is linear momentum which is denoted by ρ and the other is position vector which can be denoted by the r . Their formula or mathematical expression is given there:
L = p r
Their L denotes the angular momentum.
Torque: torque is the product of two different vector quantities, one is force which is denoted by F and the other is position vector which can be denoted by the r . Their formula or mathematical expression is given there:
τ = F r
Their τ denotes the torque.
Force of a moving charge: force in the magnetic field that can apply on the charging particle is the product of the two vectors and they are the velocity of the charged particle and the other vector is the magnetic field. their mathematical expression is given there:
F = q ( v B)
There,
F denote the force of the charged particles in the magnetic field.
q denotes the charge of the particles
v denotes the velocity of the charged particles.
B denotes the magnetic field.
Conclusion:
Like the scalar or the dot product the cross or the scalar product can play a very vital role in different fields of science and simplify complex quantities or solve complex algebraic problems in engineering, physics, and mainly in mathematics. Cross or the vector product can show the expressing relation between the algebra and the geometric calculations and solve the problems in a very efficient way in Euclidean space. After understanding the applications and the depth of the cross or the vector product, easily the complex problem can be simplified efficiently. With time the cross or vector product is more commonly used in various fields of science.