Hi friends, I hope you are well and doing good in your fields. Today we can discuss the main topic of displacement which plays a fundamental role in the motion of the object. In simple words to study and understand the motion of objects, the concept of displacement is fundamental. When the object can moved it can change its position and cover some distance and displacement. Both quantities represented the quantitative information or description of the motion of an object. Sometimes both quantities of distance and displacement are understood the same but they are not similar to each other because in distance we can describe the motion of an object as the object can be moved from one position to another position but in displacement we can measure the distance with time.
To understand the displacement it is compulsory to also understand the concept of the position of the object and the distance because after understanding both all these quantities we can efficiently understand the motion of the object in quantitative form.in different fields of physics like dynamics and kinematics displacement concepts are fundamental. Now in this article, we can also discuss the difference between distance and displacement but mainly we can explore the definition of displacement, its mathematical expression, significance, and examples.

Displacement:
Displacement provides a quantitative description of the distance of the object that can covered by the object from its initial position to the final position. Simply we can define displacement as:
"The object that can be moved and change its position from its initial position to the final position is known as displacement."
Displacement provides information about the direction of the object and also provides information on how far the object can be displaced.
Displacement is a vector quantity so that's why it can provide both magnitude and the direction of the object which are in motion.
The displacement can be represented through an arrow or also in bold letters because they are the vector quantity. For example d or as d.
Mathematical expression:
Mathematical expression and formula of displacement are given there:
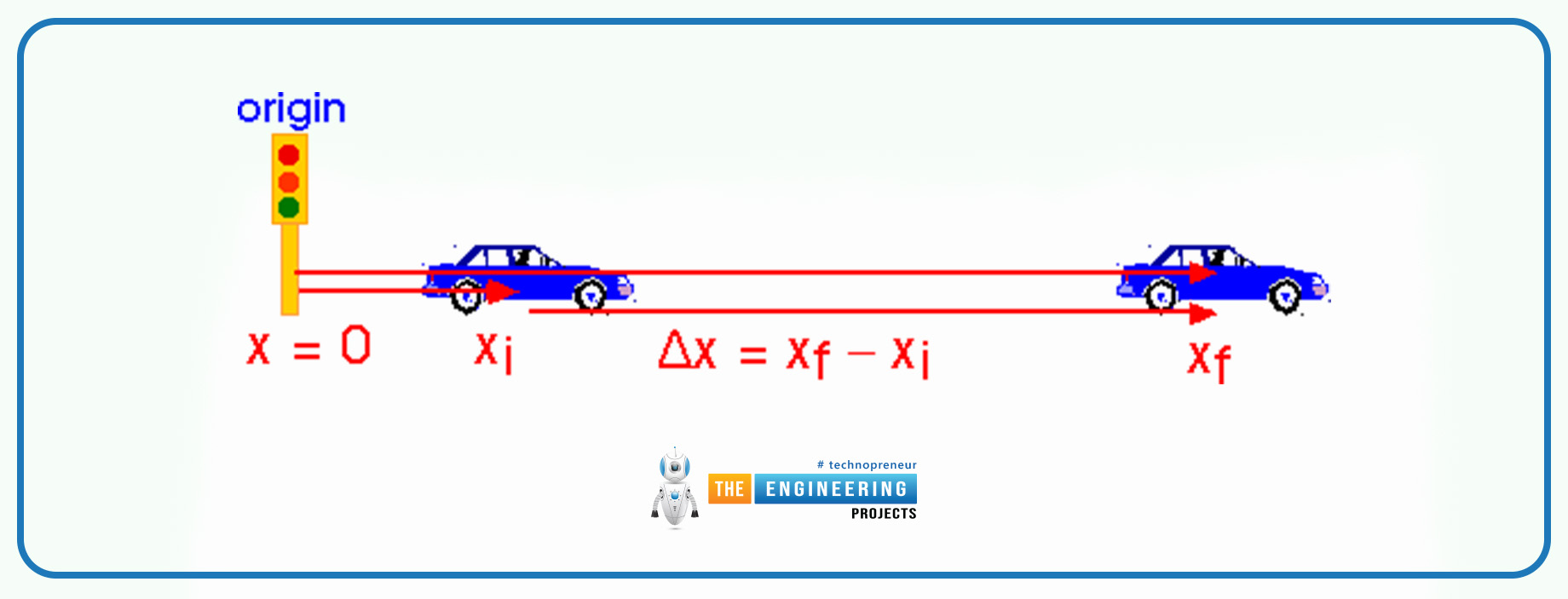
d = rf - ri
It can also be written as:
d = B - A
B and A represented the initial and the final position.
Or also as;
Δx = xf - xi
Their Δx represented the change in displacement and xf and xi represented the final and initial position of the moving object.
There,
d = represented the displacement in which the object can change the position from the initial to the final position.
rf= represented the final position in which the object can be displaced.
ri = represented the initial position in which the object can be displaced.
SI unit:
The SI unit of the displacement is the meter. And it can be represented as m.
Magnitude:
The magnitude of the displaced object is always equal to the length of the line in which the object covers the distance from the initial position to the final position.
Example:
Some examples of displacement are given there:
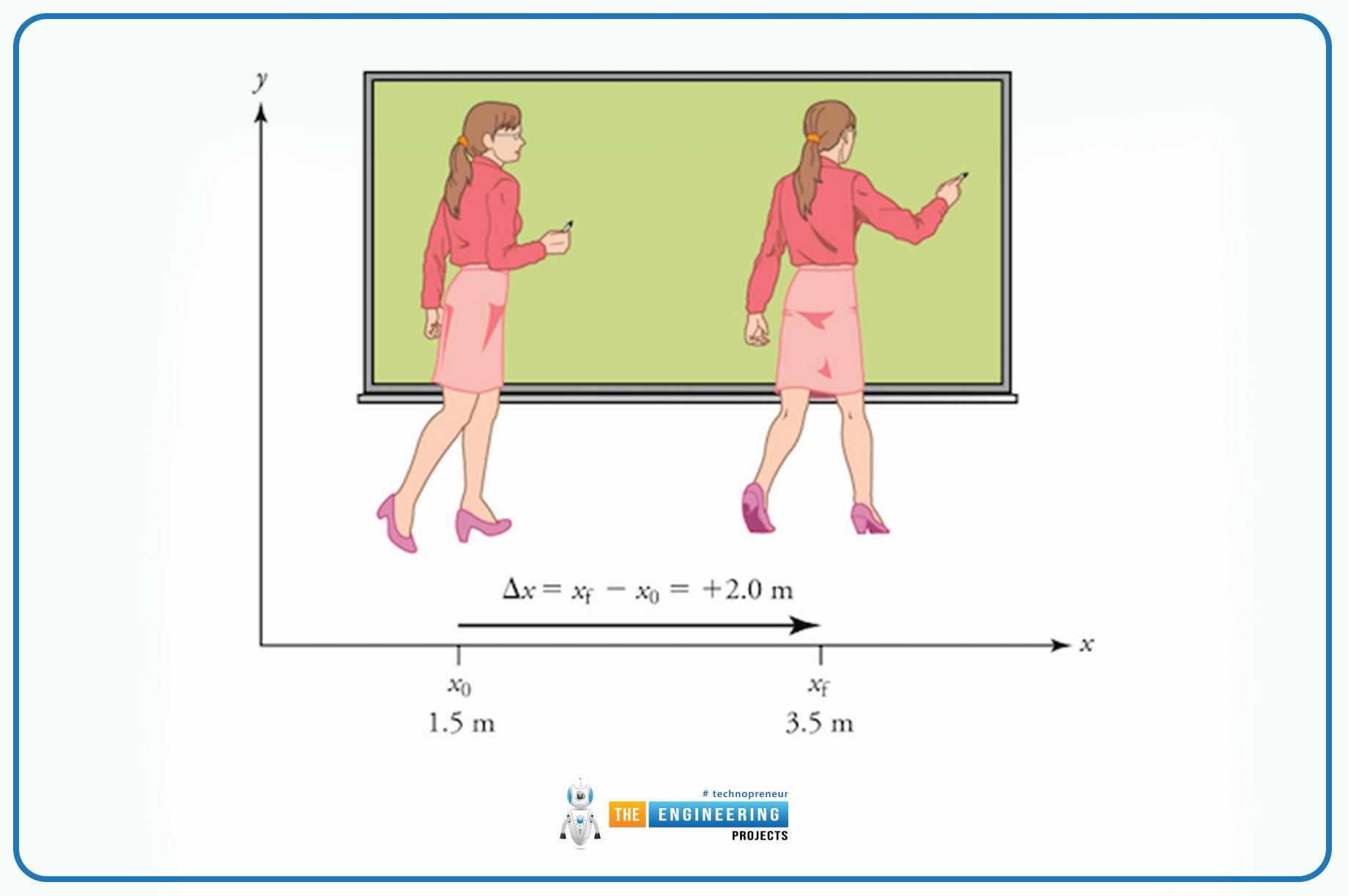
Let us consider the teacher who can take the lecture and use the whiteboard the initial point is when the teacher starts writing and the final point is when the teacher stops writing then the initial point value and the final point value can be subtracted and provide the displacement.
Concept of position (Initial and Final position)
The concept of the position of the object is compulsory to understand because it is the base or fundamental concept in the motion of the object. Even distance and displacement can be described after understanding or knowing the position of the object accurately. In the field of physics, we can discuss motion in kinematics, dynamics, and many others so it is a must to clear the concept of position.
In simple words, the position of the object is the place or area in which the object can moved or placed. In the motion of an object when the object starts its distance or work then it is referred to as the initial point or position or when the object stops moving or stops working then it can be referred to as the final point or position.
For instance, the teacher can take the lecture and use the whiteboard the initial point or position is when the teacher starts writing and the final point or position is when the teacher stops writing then the initial point value and the final point value can be subtracted and provide the displacement. Like this, every object that can be moved has some starting position where it can be placed and some final point where it stops. everything has different positions in which they are placed but in physics to understand motion, displacement, distance, and velocity it is fundamental to clear the concept of position also.

Concept of distance:
After understanding the position of the object now we discuss the main topic of distance, many people are confused or assume that both distance and displacement are the same but they are not the same they are different from each other. In simple words, distance are movement of the moving object from one point to another point and it can describe the direction also but displacement provides the both direction and magnitude of the moving object.

In the given figure the distance and displacement are both shown. The body that can start its journey from its starting point and end its some final point the whole path that can be covered by the body or the longest path that can be covered by the body or moving object is termed as the distance but the displacement is the shortest distance which can be covered by the moving body or an object.
Difference between distance and displacement:
The major differences between the distance and the displacement are given there:
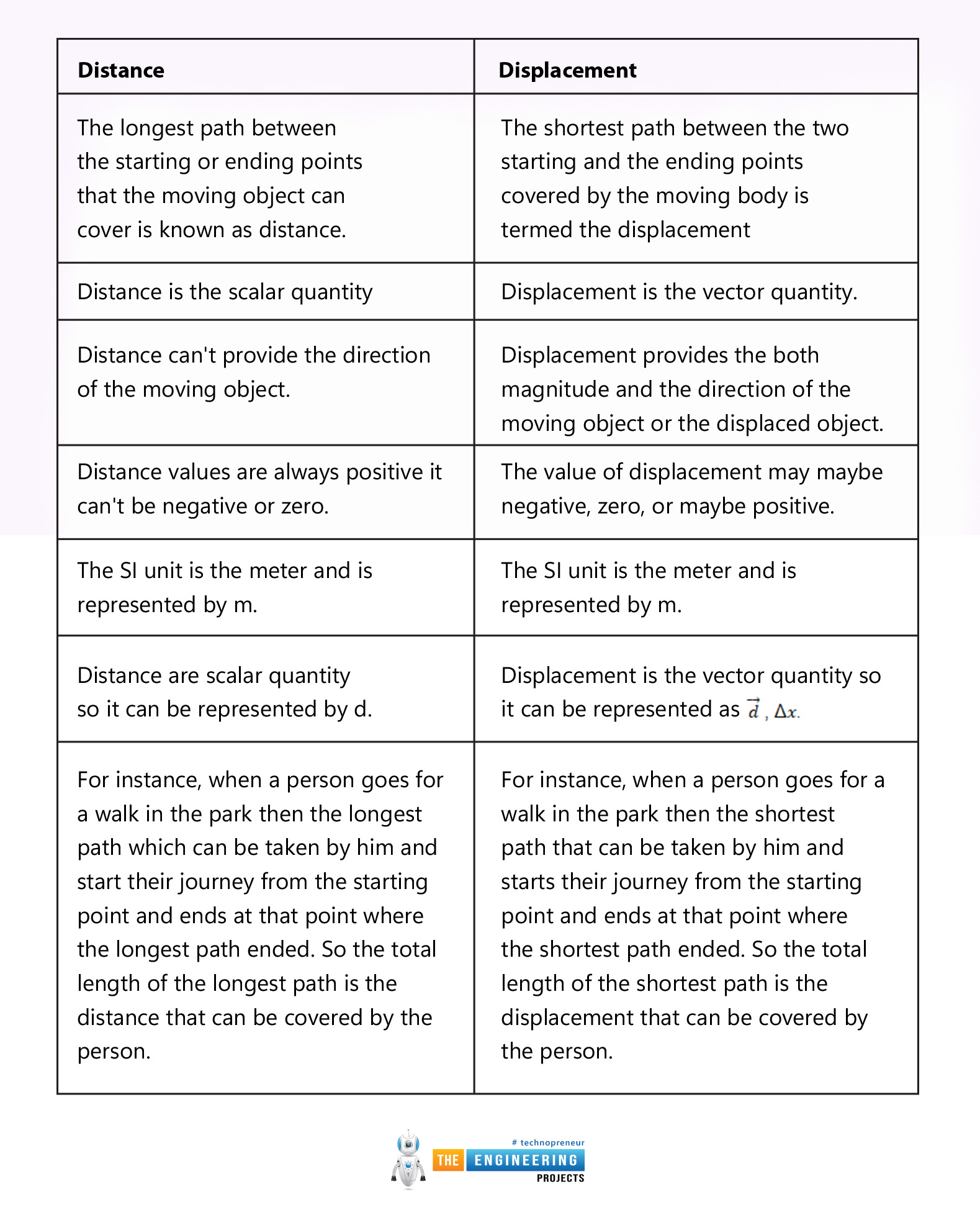
Distance |
Displacement |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Examples:
Example no 1:
Consider the person who can travel a distance of 150 m to the south and travel to the north about 205 m to do some work. Now calculate the displacement that can be covered by the person.
To find:
Displacement = Δx = d = ?
Formula:
The formula that can be used to find the displacement is:
Δx = xf - xi
Given:
xi= 0
xf = 150 m – 205 m
Solution:
Δx = xf - xi
By putting the values of the final and initial position of the object
Δx = (150 m – 205 m) - 0
Example no 2:
The four different objects can be moved and have different initial points and final points and they are opposite to each other as shown in the given figure below there:
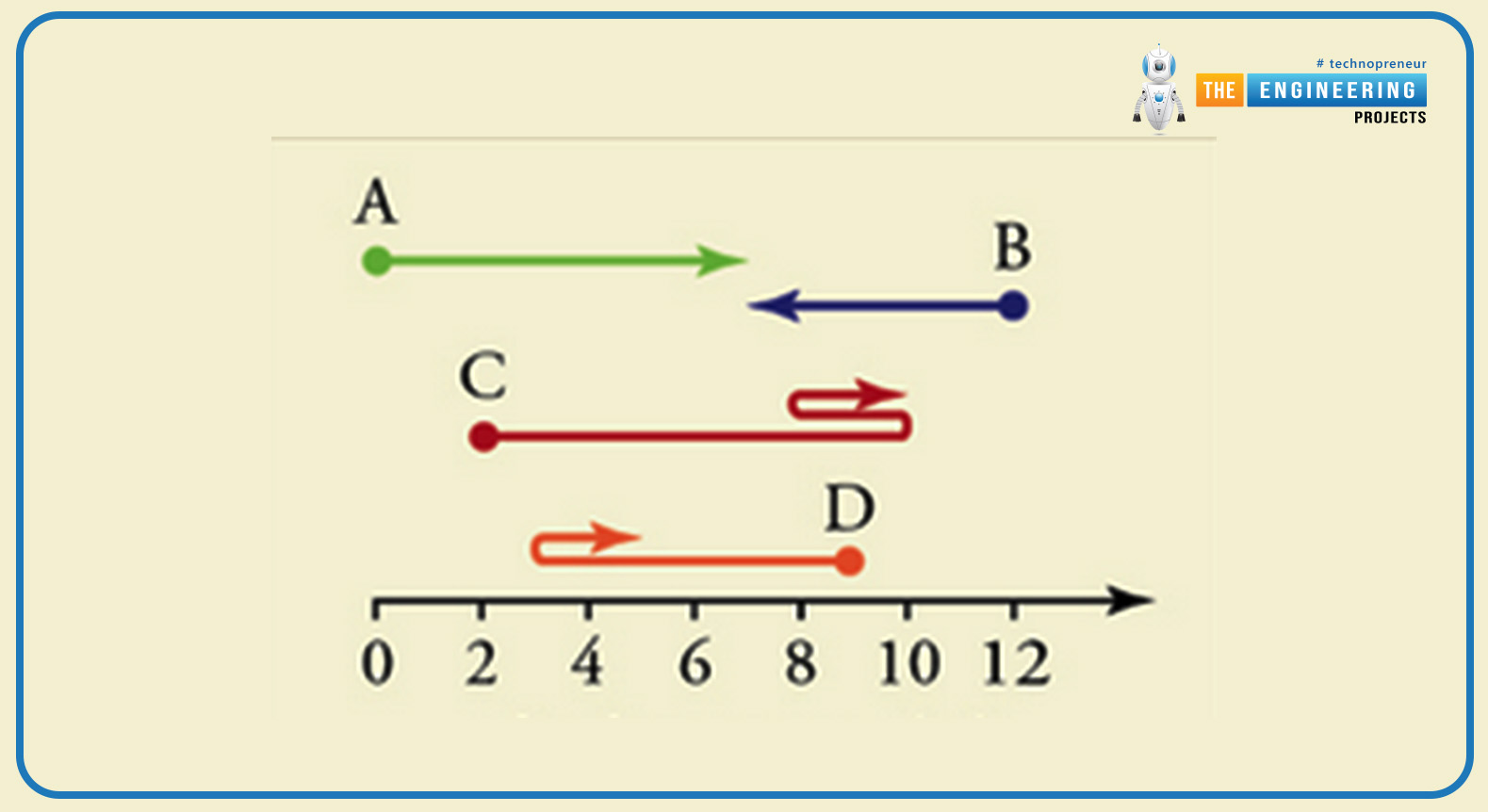
Now calculate the displacement of these four objects A, B, C, and D which can have different initial and final points.
To find:
Displacement = ΔxA = dA = ?
= ΔxB = dB = ?
= ΔxC = dC = ?
= ΔxD = dD = ?
Displacement for the object A:
Given:
According to the given figure, the initial position value and the final position value for the object A are given there:
xi = 0 m
xf = 7 m
Solution:
By using the displacement formula which is given there,
ΔxA = xf - xi
Now putting the values
ΔxA = 7 m - 0 m
ΔxA = + 7 m
Displacement for the object B:
Given:
According to the given figure, the initial position value and the final position value for the object B are given there:
xi = 12 m
xf = 7 m
Solution:
By using the displacement formula which is given there,
ΔxB = xf - xi
Now putting the values
ΔxB = 7 m - 12 m
ΔxB = - 5 m
Displacement for the object C:
Given:
According to the given figure, the initial position value and the final position value for the object C are given there:
xi = 2 m
xf = 10 m
Solution:
By using the displacement formula which is given there,
ΔxC = xf - xi
Now putting the values
ΔxC = 10 m - 2 m
ΔxC = + 8 m
Displacement for the object D:
Given:
According to the given figure, the initial position value and the final position value for the object D are given there:
xi = 9 m
xf = 5 m
Solution:
By using the displacement formula which is given there,
ΔxD = xf - xi
Now putting the values
ΔxD = 5 m - 9 m
ΔxD = - 4 m
Example no 3:
The four objects that are moved in the tiles are the different initial and final point values. The tiles' sides square are equal to 0.7 km. By understanding the given figure calculate the distance that can covered by all four objects and also calculate the magnitude of displacement of all 5 different objects.
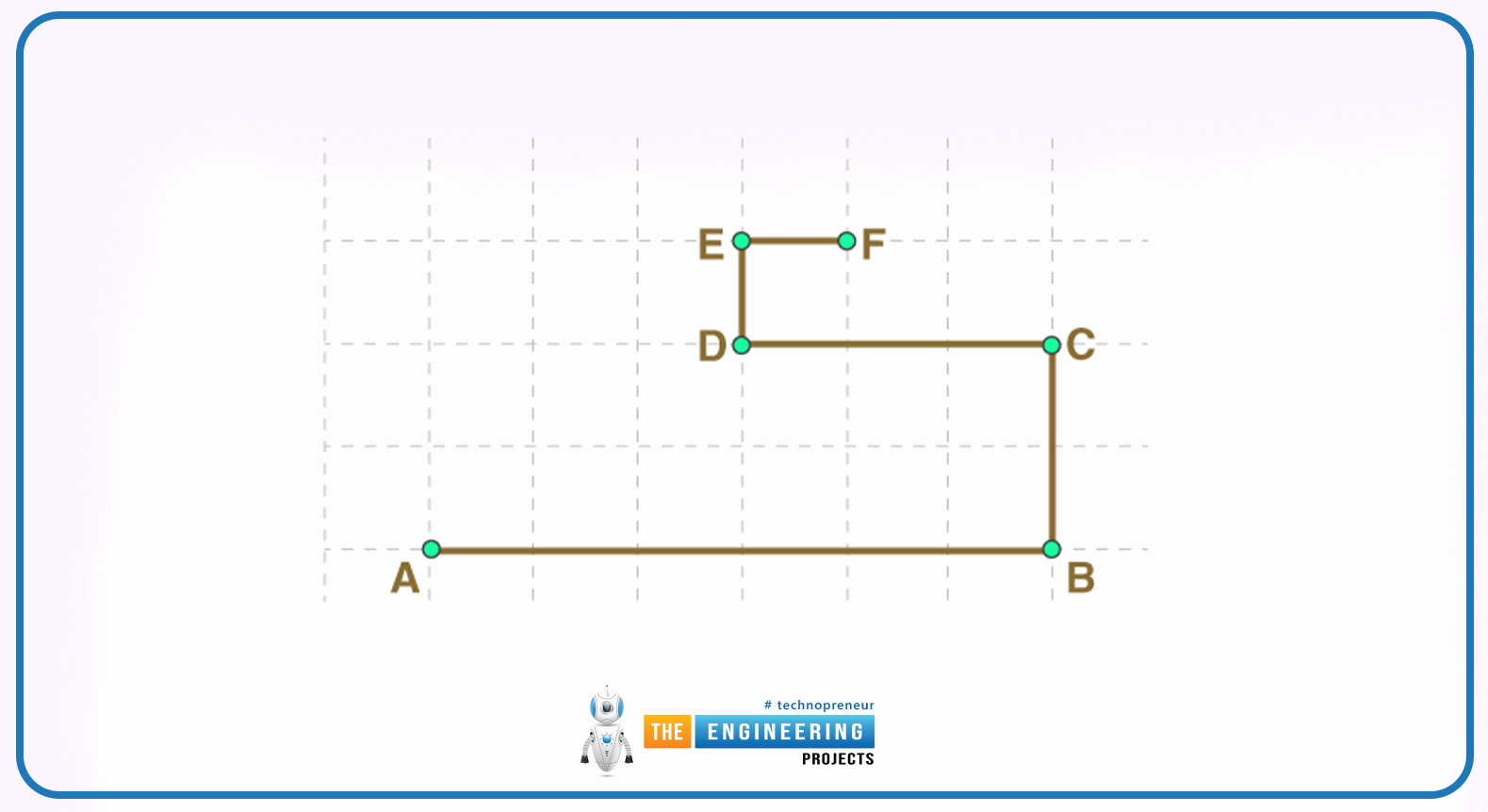
To find:
The total distance that can be covered by the 5 objects = D =?
Given:
AB = 4.2
BC = 1.4
CD = 2.1
DE = 0.7
EF = 0.7
Formula:
The formula which can be used to calculate the total distance is given there
D = AB + BC + CD + DE + EF
Solution:
By using the formula
D = AB + BC + CD + DE + EF
By putting the values then we get,
D = 4.2 + 1.4 + 2.1 + 0.7 + 0.7
D = 9.1 km
Calculation of the magnitude of the displaced objects:
We can calculate the magnitude of the displaced objects by using the Pythagorean formula which is given there:
AF2 = AH2 + HF2
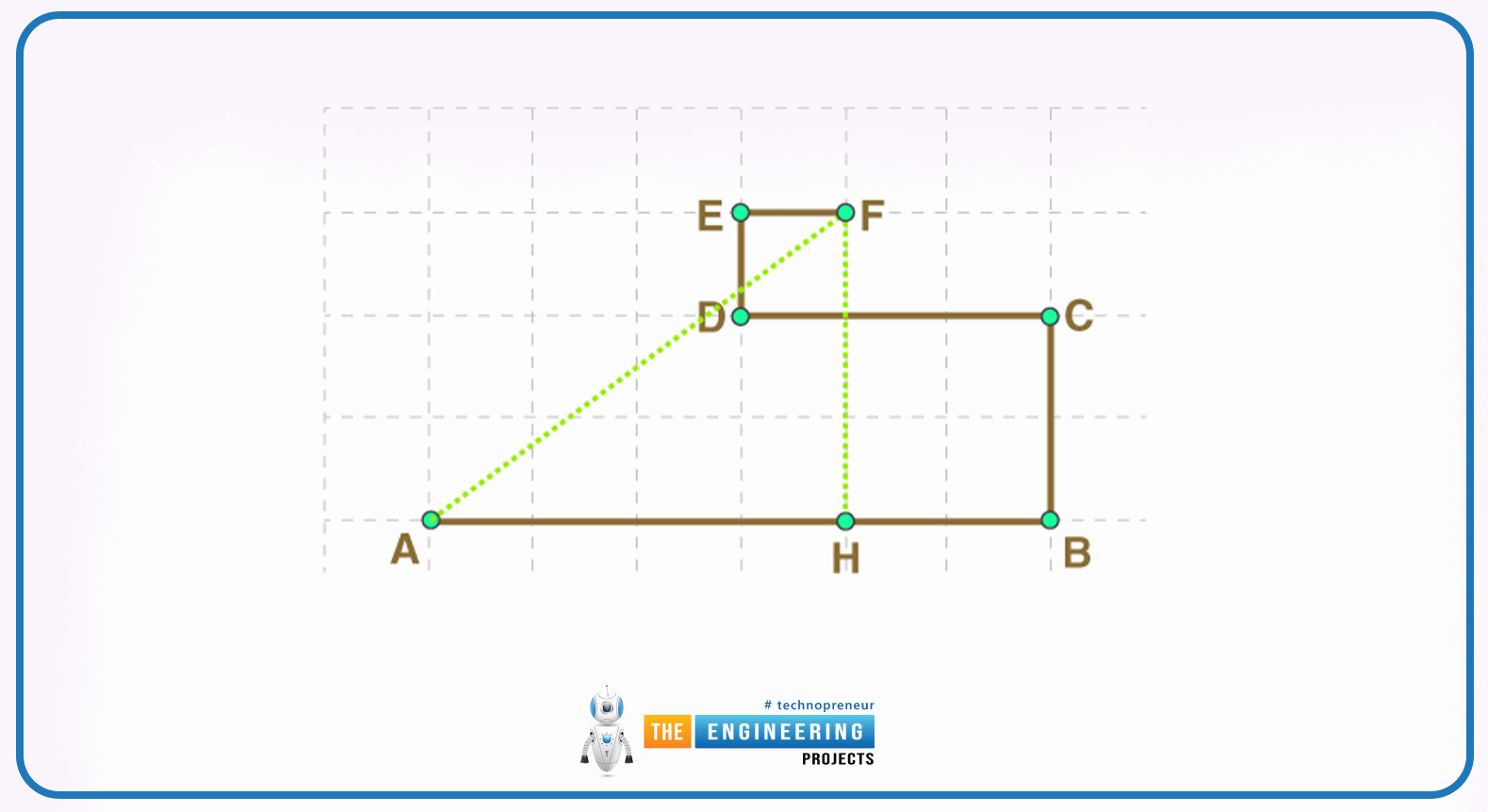
According to the given figure,
AH = 2.8
HF = 2.1
Now by using the formula,
AF2 = AH2 + HF2
Putting the values then we get
AF2 = ( 0.7 4)2 + ( 0.7 3)2
AF2 = (2.8) 2 + ( 2.1)2
AF2 = 7.84 + 4.41
AF2 = 12.25
Now taking square root on both sides
AF2 = 12.25
Then,
AF = 3.5 km
Example no 4:
The student goes to the school from house to school from point A to B then the initial point value A is 0 m and the final point value B is 9.5 m. then calculate the total displacement that can be displaced by the moving student.

To find:
Displacement = d = ?
Given:
A = initial point = xi = 0
B = final point = xf = 9.5
Formula:
Δx = xf - xi
Solution:
By putting the values in the formula
Δx = xf - xi
Δx = 9.5 - 0
Δx = + 9.5
Now we can also explore the nature of displacement its significance, graphical representation, their application in real life.
Vector nature of displacement:
All vector quantities provide both magnitude and direction. So the displacement which also has a vector nature provides both magnitude and direction. In displacement the magnitude is equal to the straight path or line that is present between the two points starting or ending and the whole path is covered by the moving object. the direction of the displaced object is the line or path that starts from the initial or ends to the final point. By using the algebraic method or formulas for adding, subtracting, or multiplying rules we can also perform these operations on displacement. Simply we can add or subtract the displacement according to the vector's algebraic rules or methods. Vector adding is complex but we can do many other mathematical operations by using different methods or by following the vectors rules efficiently.
Calculation of the displacement:
The displacement of the displaced objects can be calculated but it can depend upon their rectangular coordinate system or on the dimensions in which it can lie. Because to can use the simple displacement formula when we can calculate the displacement of displaced objects that can be lied on one dimension. But when we want to calculate the displacement of those displaced objects which can be lied on two or three dimensions we can use the vector rule or method for their subtraction. the formula which can be used to calculate the displacement are given there.
Displacement in one dimension:
The object can be moved in one direction or one dimension, Displacement is the distance that can be covered from the initial and the final point and it can easily calculated by subtracting the final value point from the initial value point. Their formula or equation is represented as:
d = xf – xi
Displacement in two dimensions:
The object can be displaced in two dimensions, Displacement is the distance that can be covered from the initial ( x1, y1) and the final point (x2, y2) along the axis or dimension of x and y. Their formula or equation is represented as:
d = ( x2 - x1) i + ( y2- y1) j
there,
i represented the unit vector on the x-dimension.
And,
j represented the unit vector on the y-dimension.
Displacement in three dimensions:
The object can be displaced in two dimensions, Displacement is the distance that can be covered from the initial ( x1, y1) and the final point (x2, y2) or the ( z1, z2) along the axis or dimension of x, y, and z. Their formula or equation is represented as:
d = ( x2 - x1) i + ( y2- y1) j + ( z2 - z1) k
there,
i represented the unit vector on the x-dimension.
j represented the unit vector on the y-dimension.
and,
k represented the unit vector on the z dimension.
Now the detailed discussion about the displacement in one dimension or two or more dimensions is given there:
Displacement in one dimension:
When the object can be displaced in one dimension then there displacement is in a straight line so that's why the displacement value may be positive or negative because its direction can slo indicating the straight line motion in one dimension with a single axis x.
Let us consider whether the object can be displaced from the starting point or the initial point value is 4 m and the final or ending point value is 6 m then we can calculate the displacement by using the formula and they are given there:
d = xf – xi
By putting values
d = 6 m - 4 m
d = + 2 m
But if the object can move backward then the displacement value is negative then their initial value is 6 and the final value is 4 then it can be written as;
d = 4 m - 6 m
d = – 2 m
The displacement value is negative.
Displacement in the two or three dimensions:
When the displacement lies in two or three dimensions then it can be represented in the form of a vector because in higher dimensions it is complex to represent the displacement in simple form so that's why it can be represented in multiple axes with vectors. These methods are mostly used to deal with the complex paths in which the objects are displaced.
Example of displaced objects in two dimensions:
The objects that are moving in the path have the starting point A, their initial point values are ( 2, 4) and the ending point values B are ( 3, 8) now find their displacement, magnitude, and direction also.
To find:
Displacement = d = ?
magnitude = d = ?
Direction = θ =?
Given:
x1, y1 = 2, 4
x2, y2 = 3, 8
Formula:
For displacement:
d = ( x2 - x1) i + ( y2- y1) j
For magnitude:
d = A2+ B2
For direction:
θ = tan-1(BA)
Solution:
Firstly we find the displacement by using the formula of displacement.
d = ( x2 - x1) i + ( y2- y1) j
By putting the values
d = ( 3 - 2 ) i + (8 - 4) j
d = 1 i + 4 j
Now use the formula of magnitude:
d = A2+ B2
By putting the values
d = 12 + 42
d = 1 + 16
d = 4.1
Now use the formula of direction:
θ = tan-1(BA)
By putting values
θ = tan-1(41)
Example of displaced objects in three dimensions:
The objects that are moving in the path have the starting point A, their initial point values are ( 2, 4, 2) and the ending point values B are ( 3, 8, 7) now find their displacement and magnitude.
To find:
Displacement = d = ?
magnitude = d = ?
Given:
x1, y1 = 2, 4
x2, y2 = 3, 8
z1 , z2 = 2, 7
Formula:
For displacement:
d = ( x2 - x1) i + ( y2- y1) j
For magnitude:
d = A2+ B2
Solution:
Firstly we find the displacement by using the formula of displacement.
d = ( x2 - x1) i + ( y2- y1) j + ( z2 - z1) k
By putting the values
d = ( 3 - 2 ) i + (8 - 4) j + (7 - 2 ) k
d = 1 i + 4 j + 5 k
Now use the formula of magnitude:
d = A2+ B2+ C2
By putting the values
d = 12 + 42 + 52
d = 1 + 16 + 25
d = 42
d = 6.5
Displacement and other relative motion:
For understanding the fundamental concept of relative motion, displacement concepts are basic. because in relative motion the displacement of the one-displaced object is assumed to the other relative motion. When the two objects are displaced or in continuous motion, then the displacement of one displaced object is relative to the other displaced object and they have the vector difference according to their displacement values.
For example:
Let us consider the two objects A and B are displaced at the path, their starting moving point values or the ending point values of object A are ( 2, 4) to ( 6, 8) and the starting and the ending point values for the object B are ( 0, 0 ) to (1, 4). They find the displacement of the object A relative to the object B.
To find:
drel = ?
d A = ?
d B = ?
Given:
A = (2, 4) (6, 8)
B = (0, 0 ) (1,4)
formula :
d A = xf – xi
d B = xf – xi
drel = d A – d B
Solution:
Firstly find the d A by using the formula
d A = xf – xi
By putting values
d A = (6-2) - (8-4)
d A= 4i + 8j
Then find the d B by using the formula
d B = xf – xi
d B = ( 1 -0 ) + ( 4 -0 )
d B = 1i + 4j
Then find the relative displacement by using the formula
drel = d A – d B
Now by putting the values
drel = (4i + 8j) - ( 1i + 4j)
drel = 3 i + 4j
Representation of the displacement in the graphical form:
Displacement can slo be represented in the form of a graph because they are vectors so that's why the vectors are complex and efficiently represented on the graphs.
In the graphical representation, the displacement is represented by putting the arrow on their starting or ending points. In the graphics; the representation of the displacement the slope represents the velocity of the displaced object.
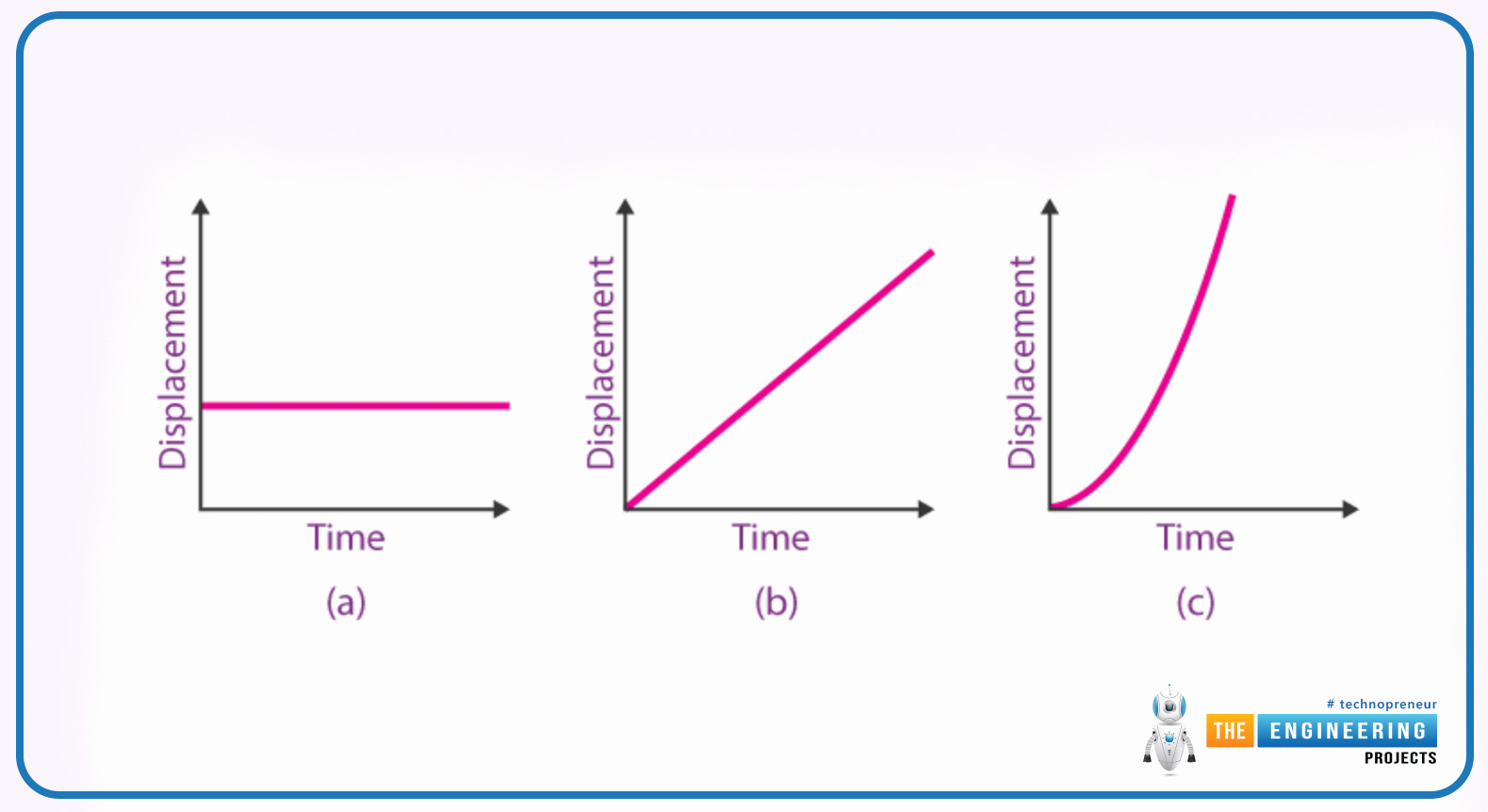
In the given graphical representation of the displacement the straight line represents the positive velocity that is constant and does not change with time but in the next graphical representation, the curve represents that the velocity changes with time and they are not constant.
The graphical representation can be changed when the displaced object's starting or final values are different with different velocities this graph representation depends upon the velocity and the starting or ending point values of displaced values.
Applications of displacement in different fields of physics:
Concept of the displacement is used widely in many different fields because it is the fundamental concept that is used in the motion of objects so that's why they are widely used mostly in the different fields of physics. some important applications of displacement in the field of physics are given there:
Sports
Engineering
Medicine
Navigation
Sports:
In the field of sports, displacement helps to analyze the performances and athlete's strategies because displacements help to increase the strength and ability of the athletes to cross the hurdles efficiently.
Engineering:
In the field of engineering, displacement concepts are the fundamental concept because when engineers design new vehicles and machine structures then they use displacement to analyze them. Displacement helps to analyze the function of the machines with specific parameters because when machines or vehicle start their motion they produce displacement so that's why firstly displacement can be analyzed.
Medicine:
In the field of medical sciences doctors and medical professionals study the motion of the different body parts of humans and animals through displacement. In biomechanics or the field of physical therapy, it is important to know about the motion of all body parts so displacement helps them to analyze or understand all motions of body parts efficiently.
Navigation:
In the field of navigation, the pilots locate their locations and sed the location to other because they analyze their location through their displacement. The sailors also locate their location with the help of the displacement vectors so that's why displacement vectors are essential and play a fundamental role in the field of navigation.
Displacements in the different coordinate systems:
The complex vectors lie in different coordinate systems so the displacements can be analyzed in a cartesian system by following the vectors rule. Mostly the displacement can be analyzed in the special coordinate system, cartesian coordinate system, and mostly in the polar coordinate system. Some unique and specific types of problems according to vectors can be resolved through them. The details are given:
Spherical coordinate system
Cartesian coordinate system
Polar coordinate system
Conclusion:
In the field of physics, displacement is the fundamental concept to understand efficiently the motion of the object and their description of the change in position of the moving object. The theoretical problems or different problems that can occur in the motion of the object can be solved efficiently after understanding the displacement crucially. The concept of displacement is the key or the basic concept to understanding displaced object movements in one dimension, navigation, medicine, engineering, or in numerous fields. After reading the whole article the reader can understand or use the displacement concept efficiently in numerous activities to understand the motion of the object.



 Physics
Physics xeohacker
xeohacker 0 Comments
0 Comments

















