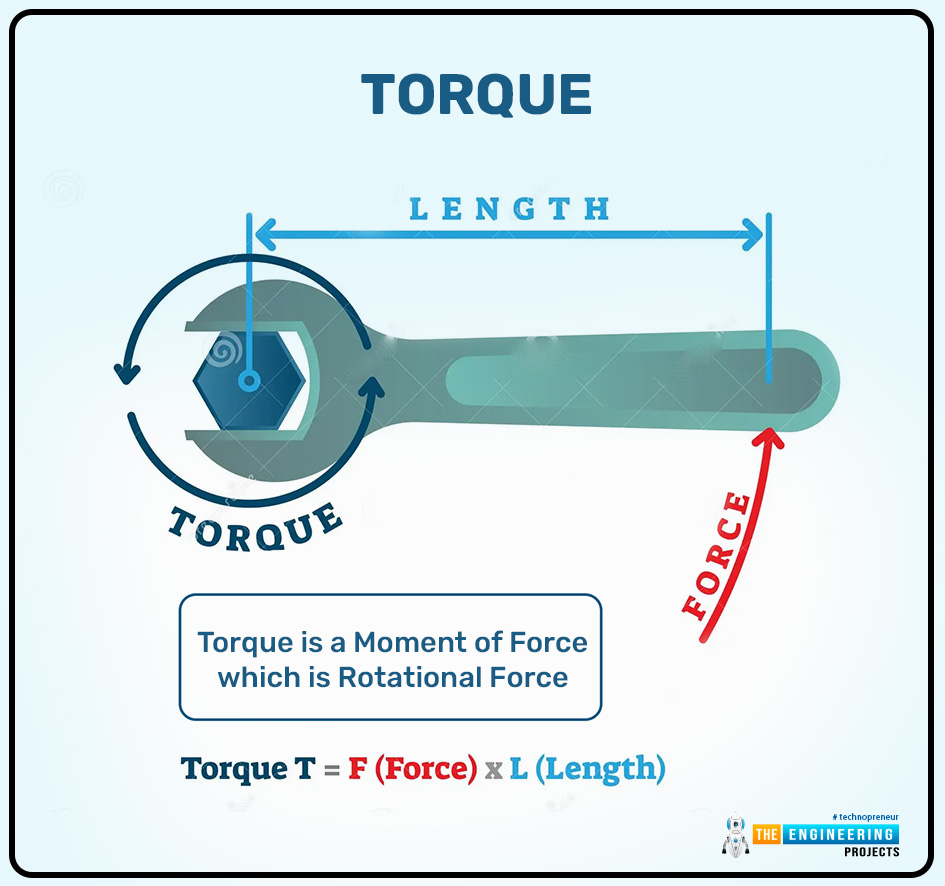
Hi readers, I hope you are all well. In the previous articles, we discussed different basic physics topics like vectors and others and now we can discuss the major topic torque in this article. Torque can also be called the rotational force or moment of the force. In physics, mechanics, and engineering torque plays a vital role and has a fundamental concept in these fields. Torque is essential to understand or describe the ability of the force of the object to rotate around its axis. The object moves with the linear force but when the object moves around its axis, some pivot point, or the fulcrum with some force then this rotational force of the object is termed as the torque.
The word torque is derived from the Latin word "torquere" which means turning or twisting. Torque describes both magnitude and direction so that is why it is a vector quantity because only vector quantities describe both magnitude and direction. Rotational dynamics The branch of dynamics can be understood through torque because the rotational force of the object is only described through torque. Torque can be represented through the symbol 𝛕. Torque can also be represented through the M. Now we can start our detailed discussion about torque, its definition, relation with other quantities, their mathematical expression, significance, applications, examples, and many other phenomena.
Background:
The idea and concept of the torque was presented by the Archimedes. The use of the lever instrument was studied by the Archmedies and when they studied them then the idea of torques was first described by him. But the term or word torque was first advised by the great scientist James Thomson. Then the experiment was done by scientist P. Thompson in the same year when the idea was described and the experiment was written in the Dynomo electric machinery book in their first edition in the 18th century, 1884.

After this, the great and famous scientist Newton can present or describe the force through which the body moves. So according to their definition when the linear force acts on the moving object and any twist occurs around their axis and changes the force of the body from linear to rotation then it is termed as the torque. For instance, the screwdriver always rotates around its axis As another example of torque the seesaw swing which can be off and on on the groping due to the imbalance of the torque.
Now torque can be used or referred to in many different fields of science to understand the rotation force of a body at the given pivot point or around its axis. Mainly the concept of the moment of force can be described in the early 18th century in 1811, but it can print in the late 18th century and the then torque is also referred to as the moment of force, and the rotational force.

Definition:
Torque can be defined as:
"the body which can move around their axis with the turning force which can be produced by the body is known as torque."
Torque can also defined as:
The magnitude of the perpendicular distance of the body from the axis of the rotation or the magnitude of the force, product of these both magnitudes are termed as the torque or moment of force:
The torque of the moment of force can also be defined as:
"the cross or the vector product of the radius or the position vector r and the vector force F".
Mathematical expression:
Torque can be written in mathematical form as:
𝛕 = r F
There,
𝛕 represented the torque and the magnitude of the torque was represented through 𝛕.
r represented the position vector and the magnitude of the position vector is represented through the r. position vector is the distance which can be measured by the torque through the point where the force is applied to the axis of rotation.
F represents the force and the magnitude of the force is represented through the F.and the force is perpendicular to the position vector r and represented by the symbol ⊥ .
The magnitude of the torque:
The magnitude of the torque can be written as:
𝛕 = r F sin
There,
𝛕 denotes the magnitude of the torque.
r denotes the magnitude of the position vector.
denotes the cross or the vector product between the two vectors
F denotes the magnitude of the force.
θ is the angle that is present between the position vector and the force, both of these are the vector quantities.
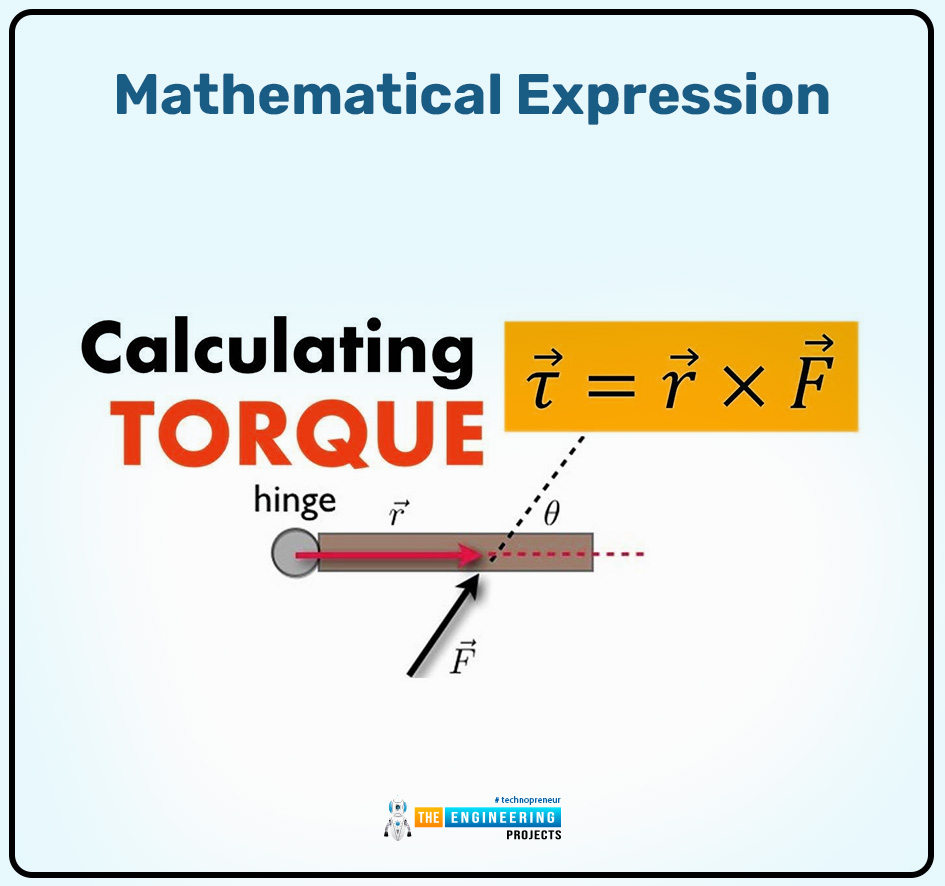
The direction of the vector quantity torque:
The direction of the torque can be represented or described through the right-hand rule. Because this rule can efficiently represent the direction of both of these vectors r and the F. According to the right-hand rule, the thumb can represent the torque 𝛕 which is the product of two different vector quantities, then the fingers of the right hand represent the direction of the position vector r and the curl fingers represent the direction of force F.

Dependence of torque:
Torque can depend on the two major factors which are given there:
Moment arm
Magnitude of the force
Both of these factors are the major factors that can directly affect the torque. The moment arm is simply defined as the perpendicular distance of the body from the line of action to the axis of rotation. And these measurements of the moment arm with the force are simply termed the torque.
Relationship of the torque with other different physical quantities:
The torque can show the relationship with many other physical quantities like power, angular momentum, and energy. Mathematical derivation which can show the relationship of torque with other quantities in detail is given there:
Energy relationship with torque:
The term torque can also be described or understood by using the law of conservation of energy. Because when the body moves with some force then it can cover some distance so they are the mechanical work that can be done by the body. In the angular displacement when the torque acts then the body is in the condition of doing work. The turning force acts on the body around its axis which is fixed with the center of mass so that's why mathematically work with torque can be expressed or written as:
W = θ1θ2 𝛕 d θ
There,
W represented the work that is done by torque.
𝛕 represents the torque through work that can be done
d is the angular displacement in which the torque or turning force can be acted
θ1 or they θ2 are the angle between the initial angular displacement point to the final angular displacement point.
Work energy principal:
The torque can show the relation with the energy or the work according to tyo the work-energy principle in which the work or energy can be changed into rotational kinetic energy on the body and it can be represented or written as:
Er = 12 I ω2
There,
Er represent the rotational kinetic energy
I represented the inertia of the body
ω2represented the angular speed of the body through which they can cover the angular momentum.
Power relationship with torque:
Power can also defined in the form of energy or work with unit joule. but the relation of the power with torque is the work that can be done in the unit of time and it can be written as:
P = 𝛕 ω
There,
P represents power.
𝛕 represents the torque.
ω represents the angular velocity through which the body does work.
represented the dot or the scalar product between the two vector quantities torque and angular velocity.
According to this mathematical expression or equation, it can be shown that the torque and the angular velocity scalar or dot product can give the output of the power. the torque in the relationship of the power was dependent upon the angular velocity or the speed. But the torque does not depend on the velocity decreased or maybe increased but it only depends upon the angular velocity. The force also depends upon the velocity of the object on the acceleration or the speed.
Confirmation derivation:
The work that can be done on the body when the random variable force acts on the body in the liner displacement or the force which can act on the body with the respect of elemental displacement then it can be written as:
W = s1s2 F . ds ……. (i) equation
There,
S1 and S2 are the initial and the final linear displacements that can be covered by the object during the work.
F represented the force
ds represented the elemental linear displacement.
So,
The elemental displacement ds are also equal to the cross or vector product of the radius and the angular displacement and written as:
ds = d θ r
There,
r represented the radius
d θ represented the angular momentum
Now put the value of the ds in the equation (i)
W = s1s2 F . d θ r
Now as shown in the equation the triple scalar product integers are shown and it can be also written as:
F . d θ r = F r . d θ
If we know that the radius or the angular momentum with force is equal to the torque then it can be written as:
W = s1s2 𝛕. d θ
But if both quantities, torque and angular momentum can lie in the same direction then the angle between them is cos, and their magnitude can be written as the:
= 𝛕. d θ
= r . d θ cos0
= 𝛕 d θ
Then it can be written as:
W = s1s2 𝛕 d θ
Angular momentum relationship with the vector torque:
Angular momentum which can be acted on the body can be determined through the torque that can act on it and it can be written as:
𝛕 = dLdt
There,
𝛕 represented the torque
L represents the angular momentum
And the t represented the time with the displacement.
Or the angular momentum is also equal to the inertia of the moment and the angular speed and it can be written as:
L = I ω
I represented the moment of inertia and the w represented the angular speed.
And the moment of inertia I is also equal or written as:
I = m r2
Then the total net torque can be written as:
𝛕net = I1w1e1 + I2w2e2 + I3w3e3 + I1w1 de1dt + I2w2 de2dt + I3w3de3dt
𝛕net= Iw + w (Iw)
Then it can also be written as:
deidt = w ei
This equation can be used for newtons law but in some problems, there are only inertia and angular momentum then in a simple way, we can write them as the:
𝛕 = I a
There,
𝛕 represented the torque, I represented the inertia, and the a = w represented the angular velocity or the speed.
This equation can also be called the Newton's second law.
Confirmation derivation:
Simply, the angular momentum for a single particle can be defined or written as:
L = r p
There,
L represented the angular momentum of the single particle
r represented the position vector
p represented the linear momentum of the single particle.
But when we can write the angular momentum for time then mathematically it can be written as:
dLdt = dpdt r + drdt p
As shown in the given mathematical equation when we can split the equation into its components and then we can use the product rule of vector because the force is represented the rate of change in the momentumdpdt and the drdt change in the position of the quantity is represented through the velocity symbol v. then it can be written as:
dLdt= F r + v p
There,
V represented the velocity and the F represented the force. Now as shown in the given equation both vector quantities velocity v and the angular momentum p are parallel to each other so they are equal to zero 0 and it can be written as:
dLdt= F r
Now as shown in the given mathematical equation force and the position vector are equal to the torque and when we apply the Newton law then it can be written as:
𝛕net = dLdt= F r
Now through this equation, it can be proved that the torque has a significant relationship with the angular momentum of the single particle. This mathematical equation is the generalized proof of the torque and the angular momentum along the mass.
Unit, symbol, and dimension of torque:
The units, symbols, and the dimensions of the torque are given there:
units :
For the quantity torque, many units can be used but some major units that can used to express the torque are given there:
Nm ( newton meter)
Dyn . cm ( dyne - centimeter) This unit can be used in the CSG system to express the torque.
Pound foot represented by ( Ibf- ft)
Pound inch, this unit can be used to measure the small torque measurements and represented by ( Ibf- in).
Foot-pound can be represented through Ib- ft.
Like the foot-pound, the torque can also be represented through inch-pound and represented through the in-Ib.
SI unit of the torque:
The SI unit of the torque can be written as:
kg . m2 . s-2 ( kilogram meter square per second square)
Dimension of the torque:
Dimension of the unit torque is written as:
ML2T-2
Calculating the torque:
Torque can be calculated and depends upon some major factors but some major formulas that are used to calculate the torque for the single force and for the multiple force are given there:
Torque for a single force:
When a single force applies or acts on the body with some distance from their fixed axis of rotation, and the force that acts on the body is perpendicular to the position vector r, then the torque can be written as:
𝛕 = r F
But if the force is not perpendicular to the position vector r then it can be written as:
𝛕 = r F sin θ
there,
θ can represent the angle between the force and the position vector.
Torque for multiple forces:
When the multiple forces act on the body or object then the torque can be calculated through their vector sum and written as:
𝛕net = 𝛕i
There,
𝛕net represented the total sum of the torque that can act on the body with multiple forces.
and,
𝛕i = ri Fi
Calculation of the torque on the rigid body:
Now we can calculate the torque that can act on the rigid body.
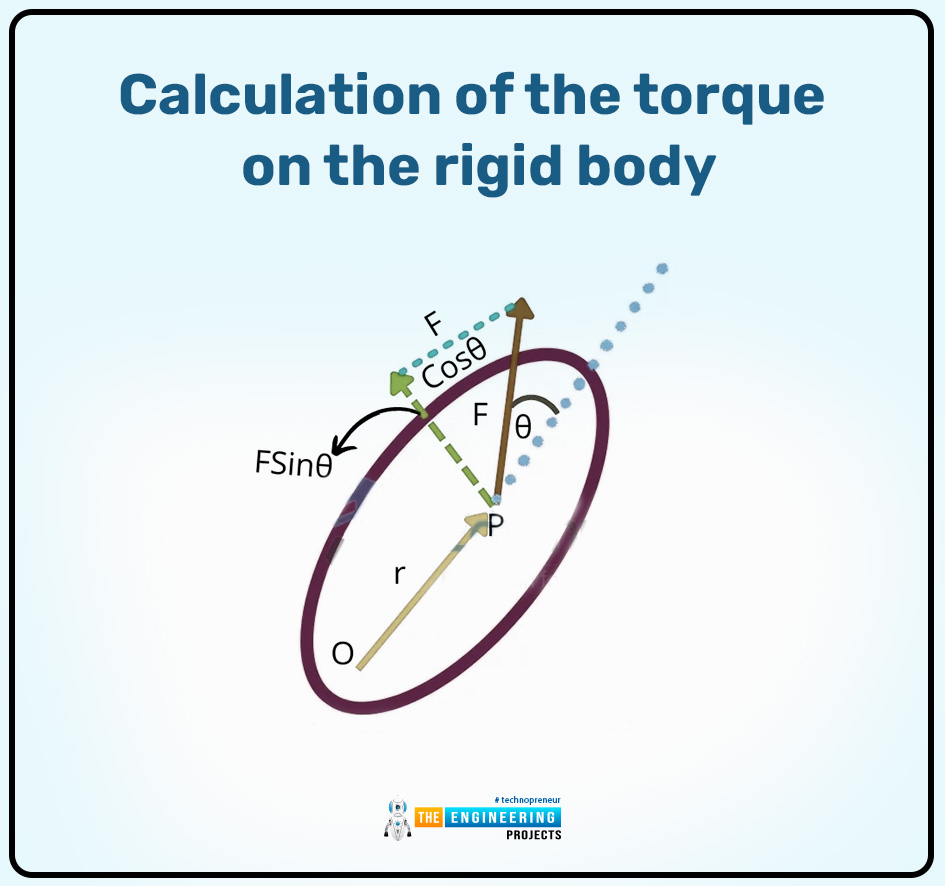
As shown in the figure, let us consider the rigid body. According to this figure, the force F acts on the object at the point p, r is the position vector according to the point p, and the angle between the force and the position vector r is represented through the Now we can calculate their torque by their resolution.
Force F resolution:
In the above figure, we can see the components of the vector according to the rectangular components and then it can be written as:
F cos θ = this is the component of the force in the rectangular component which can act in the direction of the position vector r.
F sin θ = this is the component of the force in the rectangular component which can be perpendicular to the position vector r.
The torque due to the force:
As shown in the above equation, the F cos θ and their line of action can pass through the point O, and this rectangular component due to the line of action becomes zero 0. So that is why the force that can be acted on the body is equal to the F sin θ which can produce the torque and it can be written as:
𝛕 = r( F sin θ)
𝛕 = r F sin θ
Or when we can write with their magnitude or in vector form then it is as:
𝛕 = r F sin θ n
Also, it can be written as:
𝛕 = r F
Substitutes:
After the component of force then we can write the rectangular component of the position vector r. It can be written there as:
r cos θ = the component of the position vector r along with the direction of the force.
r sin θ = the component of the position vector r perpendicular to the vector force F.
The torque due to the force F:
When the torque is produced due to the force, in this case, we can write the torque as:
𝛕 = l F
there,
L is equal to the moment arm and it can be written as:
l = moment arm = r sin θ
So it can be written as
𝛕 = ( r sin θ) F
𝛕 = r F sin θ
In the magnitude of the vector form it can be written as:
𝛕 = r F sin θ n
Also, it can be written as:
𝛕 = r F
Examples:
A wrench ( spanner) is used to tighten the nut. The spanner moves around its axis of rotation with some force so it can produce the torque.
The swing seesaw can move up and down on the ground due to the imbalance of the torque because its center is fixed so it can move at the line of action and produce the imbalance torque.

Important points for torque:
For the rotational motion of the body, torque is the major or counterpart of the force that can act on the moving object.
The body can be moved through the linear motion and the angular motion in which force can be acted, the force is the same as the torque.
The linear acceleration can be described or determined through force and the angular acceleration can be determined or described through the torque.
The torque will be positive if the rotational motion of the object occurs in the anti-clockwise direction, and the torque will be negative if the rotational motion of the object occurs in the clockwise direction.
Application of torque:
Torque can play a very fundamental role in many different fields some of their applications in different fields with detail are given there:
Robotics
Mechanical system
Sports and biomechanics
Structural engineering
Their detail is given there:
Robotics:
Torque plays a vital role in the robotic system. Because by the help or understanding of the torque the movement of the robots through their arms or joints is controlled efficiently. Torque helps to determine or describe the force that can act on the joints of the robot through which they can do rotational motion and help to control all movements of the robots precisely or efficiently.
Actuators: actuators are the systems in the robots that can convert the energy to the motion through which the robots can be moved. The functions of the robots are controlled efficiently through the torque. Torque also helps to choose the best and appropriate systems and actuators for making the robotic system accurate or precise.
Robotic arm: the joints are moved through the rotational force which is torque so that's why all joints or arms of the robot have some specific torque value through which they can move or complete their specific movement efficiently.
Mechanical system:
In the field of mechanics which is the branch of physics, torque are fundamental concept for designing engines or gears, and turbines or generators. Because in these given systems the engines can work with some force which is termed as torque and it can be moved or run through the rotational motion, the efficacy and the output of these systems can be measured also through torque.
Gear system: the efficient and precise gear system can be designed by determining the torque because the torque can be transmitted to the near components through which the system can run efficiently.
Engines: in the mechanical system the engine's efficiency and ability can be determined through the torque. Because the torque describes the ability and the capacity of the engine's acceleration and the capacity to carry the load. So to make efficient and design efficient engines torque can be used.
sports and biomechanics:
Torque can play an essential role or help to determine or analyze the movements of the human joints because the joints can do rotational motion. Through torque athletic performance can also be improved or managed. Torque also helps to understand which muscles can apply the force on the joint to do movements and through which muscle we can control the movement and prevent injury chances.
Injury prevention: by understanding the torque detail we can design the many equipment that can help to decrease the risk of injury and also prevent the human or athlete from injury. Torque also helps to understand which muscles can apply the force on the joint to do movements and through which muscle we can control the movement and prevent injury chances.
Athletic performance: the torque is produced by the muscle and these forces act on the joint through the movements that occur, by understanding the muscles that produce torque helps to improve performance, and with training the athlete can maintain or improve their skills efficiently.
Structural engineering:
The structure stability and the system ability can be determined through the torque. In structural engineering, bridges, buildings, and other designs are made after understanding the torque because it can help to understand the ability of the object to carry the load.
Bridges: when the engineers are designed to make the bridges they determine the torque because it can help them to find or observe whether the bridges can carry the load and are safe to use or not.
Advanced topics in which torque is used:
Torque can be used in many different advanced topics because the concept of torque can be presented in the 18th century and with time it can be used in many different fields some are given there:
Torque in electromagnetic systems:
Generators:
Electric motors:
Precession:
Gyroscopic effects:
Gyroscopes:
Experimental measurements of torque:
Measurements of torque are very essential so, to measure the torque efficiently and take precise and accurate measurements many different instruments and devices are used some of these are given there:
Dynometers:
Dynamometers are the instruments that are used to measure the efficiency of the engines and the output of the engines with torque efficiently. Many types of dynamometers are used to measure these torque measurements some are given there:
Chassis dynamometer
Engine dynamometer
Torque wrenches:
Used to measure the torque or also tighten the nuts through the wrenches by applying force on it.
Torque sensors:
Torque sensors which are also termed torque transducers, are instruments or devices that can be used to measure the torque of all rotating objects or systems. Torque sensors are mostly used in the automotive to control or monitor the torque. some types are given there:
Rotary torque sensor:
Strain gauge sensor:
Conclusion:
Torque plays a vital role in different fields of science. Torque made the relationship and described the relationship between the linear motion and the rotational motion efficiently. Through understanding the torque we can also understand how the force acts on the body and how the object can be moved around its axis and do the rotational motion efficiently. Torque can be used in our daily life when we used the screw gauge, wrench, and others then they do the rotational motion and produced the torque efficiently. In the era of modern science, torque plays a fundamental role in simplifying complex problems efficiently. After understanding and reading their definition, and mathematical relationship with other physical quantities we can achieve great knowledge about this ubiquitous force that plays an essential role in the physical world.



