Hi friends, today we can discuss the main topic which is Newton's law of motion. Newton's Laws of Motion structure the foundation of traditional mechanics, a part of physical science that depicts the way of behaving of actual bodies. These regulations give a structure to understanding what powers mean for the development of items, from regular encounters to the mechanics of heavenly bodies.
The meaning of Newton's Regulations couldn't possibly be more significant; they offer a straightforward yet significant clarification of how powers interface with issues. These standards are not simply scholarly; they support incalculable parts of our day-to-day routines and mechanical headways. From the working of vehicles and hardware to the direction of satellites, Newton's Regulations give the fundamental comprehension expected to break down and foresee movement. This understanding is pivotal for fields going from design and material science to cosmology and then some.
Historical Context and Isaac Newton's Contribution:
The plan of these regulations is credited to Sir Isaac Newton, a crucial figure in the logical upset of the seventeenth 100 years. Newton's work in the last part of the 1600s finished in the distribution of "Philosophiæ Naturalis Principia Mathematica" in 1687, usually known as the Principia. In this original work, Newton explained three regulations that portray the connection between a body and the powers following up on it, alongside the body's movement because of these powers.
Newton's experiences were historic. Before his work, the comprehension of movement was divided and missed the mark on binding together hypotheses. By presenting a bunch of regulations that could be generally applied, Newton not only settled a large number of the irregularities in the overarching hypothesis yet in addition laid the basis for future logical investigation and development. His commitments reached out to past movements, affecting different regions, for example, optics and science, subsequently hardening his heritage as perhaps one of the most compelling researchers ever.
Newton's First Law (Law of Inertia):
Newton’s First Law of Motion also known as the Law of inertia is a vital and basic law that describes the state of affairs of objects when there is no force acting or the net force acting on an object. This law identifies the basis for understanding motion, thus stating what can be considered a simple but deep truth of the world.
Definition and Explanation:
The Law of Inertia, as articulated by Sir Isaac Newton, posits that an object will persist in a state of rest or uniform motion in a straight line unless compelled to change by the action of an external force. Put simply, absent any alterations to its environment, an object at rest will remain stationary, although an object in motion will continue along its trajectory without deviation or change in speed. This fundamental principle underscores the concept of inertia, wherein objects exhibit a propensity to oppose modifications to their state of motion.
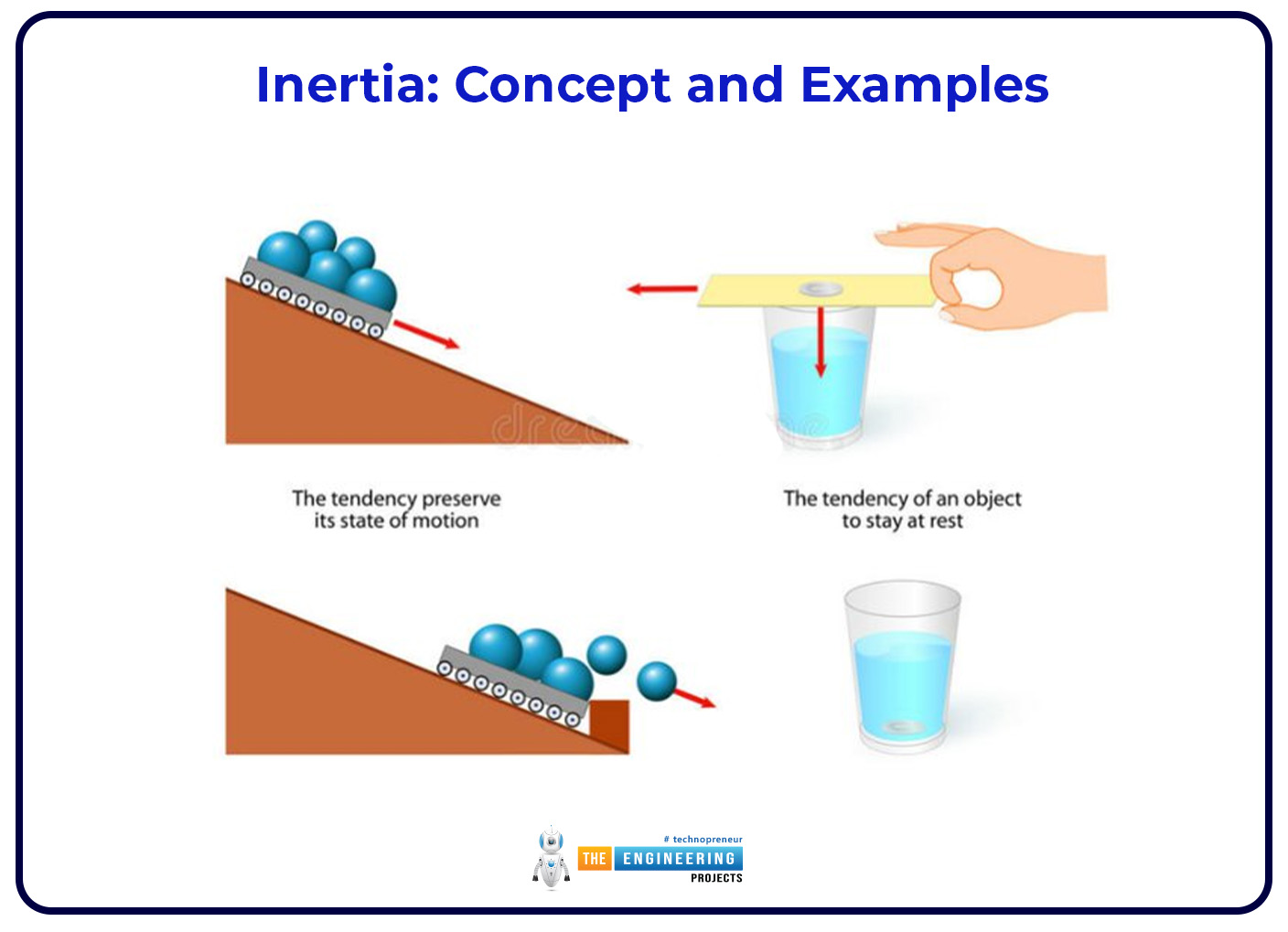
Inertia: Concept and Examples:
Inertia represents an object's tendency to resist changes in its state of motion. It is directly proportional to the mass of the object, meaning that a greater mass results in a greater inertia, necessitating a larger force to induce a change in its motion. This concept is exemplified in everyday scenarios: for instance, the comparative ease of pushing a bicycle in contrast to a car can be attributed to the car's higher mass and, consequently, its increased inertia.
In practical terms, the manifestation of inertia can be observed when riding in a vehicle that abruptly halts. In the absence of a seatbelt, the occupants continue to move forward despite the vehicle's cessation, revealing the inertia of their bodies. Similarly, an unmoving book on a tabletop persists in its position until subject to an external force, distinctly illustrating that objects remain stationary unless acted upon by a force.
Applications in Daily Life and Engineering:
Understanding dormancy is significant in day-to-day existence as well as in different fields of design. In transportation, safety belts and airbags are planned in light of inertia, assisting with preventing travelers from pushing ahead in a crash. In design, the idea of idleness is fundamental while planning structures that need to endure dynamic powers, for example, extensions and high rises, guaranteeing they stay stable under differing conditions.
Dormancy likewise assumes a part in space investigation. For space apparatus, whenever they are gotten rolling in the vacuum space, they keep on going in an orderly fashion at a steady speed except if followed up on by another power, like gravity or impetus frameworks. This rule considers the preparation of significant distance space missions with insignificant fuel utilization. These models exhibit the inescapability of Newton's first law Regulation in both regular encounters and high-quality mechanical applications, highlighting its major job in how we might interpret the actual world.
Newton's Second Law ( Law of Acceleration):
A quantitative description of the changes that a force can cause in the movement of a body is given by Newton's Second Law of Motion. A mathematical foundation for understanding how objects accelerate is provided by the clear and direct relationship between force, mass, and acceleration.
Mathematical Formulation:
Newton used the term "motion" to refer to the quantity that is now known as momentum, which is dependent on the quantity of matter in a body, its velocity, and its direction of motion. The product of a body's mass and velocity is its momentum in today's notation:
𝑝 = 𝑚𝑣
where the three amounts are subject to fluctuate over time. In its current incarnation, Newton's second law states that the force's magnitude and the momentum's time derivative are equal and point in the same direction:
F=dpdt
Now we put the values of momentum ( ) in the above equation;
F=d ( mv )dt
The force is equal to the product of the mass and the time derivative of the velocity, or acceleration if the mass 𝑚 is constant throughout time and the derivative solely affects velocity;
F=m dvdt
As acceleration ( a ) is formulated as;
a=(dvdt)
So,
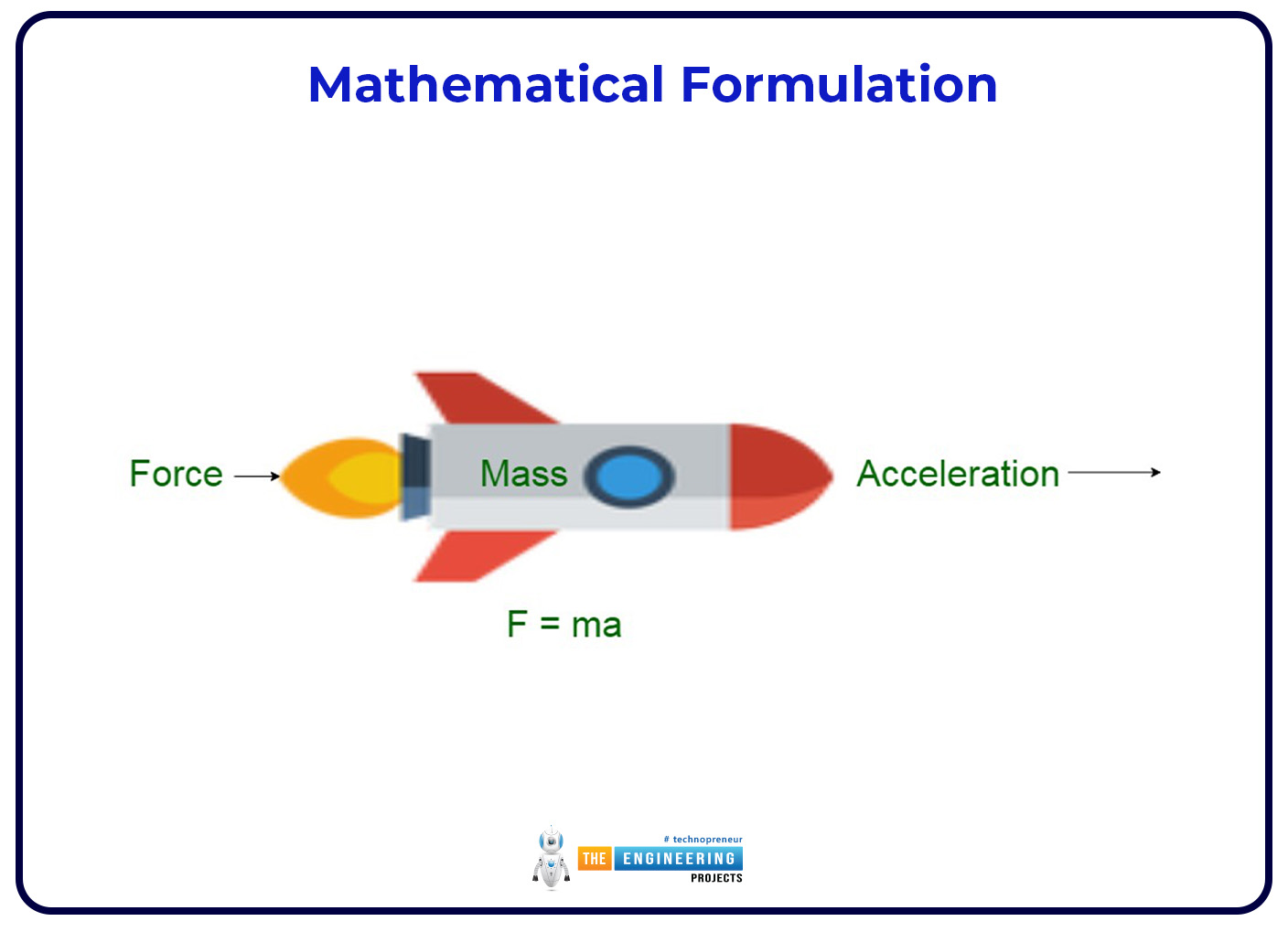
F=ma
This formula demonstrates that an object's acceleration is directly proportional to the force applied to it, with mass serving as the proportionality constant. In essence, this rule measures the impact of forces: given a fixed mass, an item will accelerate more quickly when greater force is applied to it.
The formula (F = ma), in which (m) is the object's mass, (a) is the acceleration generated, and (F) is the net force applied to the object, encapsulates the core of Newton's Second Law.
when the acceleration is the position's second derivative concerning time, this is shown as,
F=m d2sdt2
Although the forces acting on a body add up as vectors, then the total force exerted on the body is dependent on the individual forces' magnitudes and directions. According to Newton's second law, a body is considered to be in mechanical equilibrium when its net force is equal to zero and it does not accelerate. If the body stays close to a mechanical equilibrium even when its location is slightly altered, then the equilibrium is stable.
Understanding Force, Mass, and Acceleration:
To fully understand this law, it's important to understand the key terms:
Force
Mass
Acceleration
Force (F):
Pushing or pulling applied to an object, expressed in Newton's (N). An item may begin to move, halt, or alter direction as a result of it.
Unit of force:
The formula for defining force unit in terms of the three fundamental units of mass, length, and time is Fnet = ma. The newton, or N, is the SI unit of force. One N is the force required to accelerate a system with a mass of one kilogram at a speed of one meter per second. Combining these gives,
1 N =1 kg ⋅ m/s2
Although the newton is the unit of force used practically everywhere in the world, the pound (lb), where 1 N = 0.225 lb, is the most often used measure of force in the United States.
Weight and the Gravitational Force:
When Something falls, it expedites toward Earth's midpoint. According to Newton's second law, an object's acceleration is caused by a net force acting on it. The gravitational force, often known as an object's weight, or 𝑤 is the net force on a falling object if air resistance is insignificant. Since weight has a direction, it may be represented as a vector 𝑤. Since gravity always points downward, 𝑤 is oriented in that direction. The symbol for weight magnitude is 𝑤. Galileo had a key role in demonstrating that all things fall with the same acceleration (𝑔) when there is no air resistance. An equation relating to the magnitude of weight may be derived by applying Newton's second law and Galileo's finding. study an object with mass 𝑚 that is descending toward Earth. It is subject simply to the amount 𝑤 downward force of gravity. According to Newton's second law, an object's net external force magnitude is equal to 𝐹net = 𝑚𝑎.
Since gravity's downward force is all that the thing feels, Fnet = w. We are aware that an object's acceleration as a result of gravity is equal to g, or g = a. The weight equation, or the gravitational force acting on a mass m, may be obtained by substituting these into Newton's second law:
𝑤 = mg
We refer to an item as being in free fall when its weight acts as its net external force. In other words, gravity is the only force acting on the item. In the actual world, there is always an upward force that is air acting on items as they fall toward Earth, therefore they are never completely in free fall.
Mass (m):
a measurement of an object's mass, usually expressed in kilograms (kg). It also expresses an object's resistance to changes in motion, called inertia. Mass is an attribute of the item itself, not its position, and is a scalar quantity, which means it has no direction. The unit of mass is kilograms (kg).
The mass of an item remains the same whether it is in space, on the moon, or Earth. On the other hand, the object's weight will vary under these various conditions. According to our daily experiences, an object has mass if it is heavier, or has greater weight. Therefore, based on our experience, a baseball, for instance, has greater mass than a balloon. We may understand mass in a useful way by relating it to weight, provided that we do not consider it to be the same thing. We can more precisely link force and motion using this idea of mass.
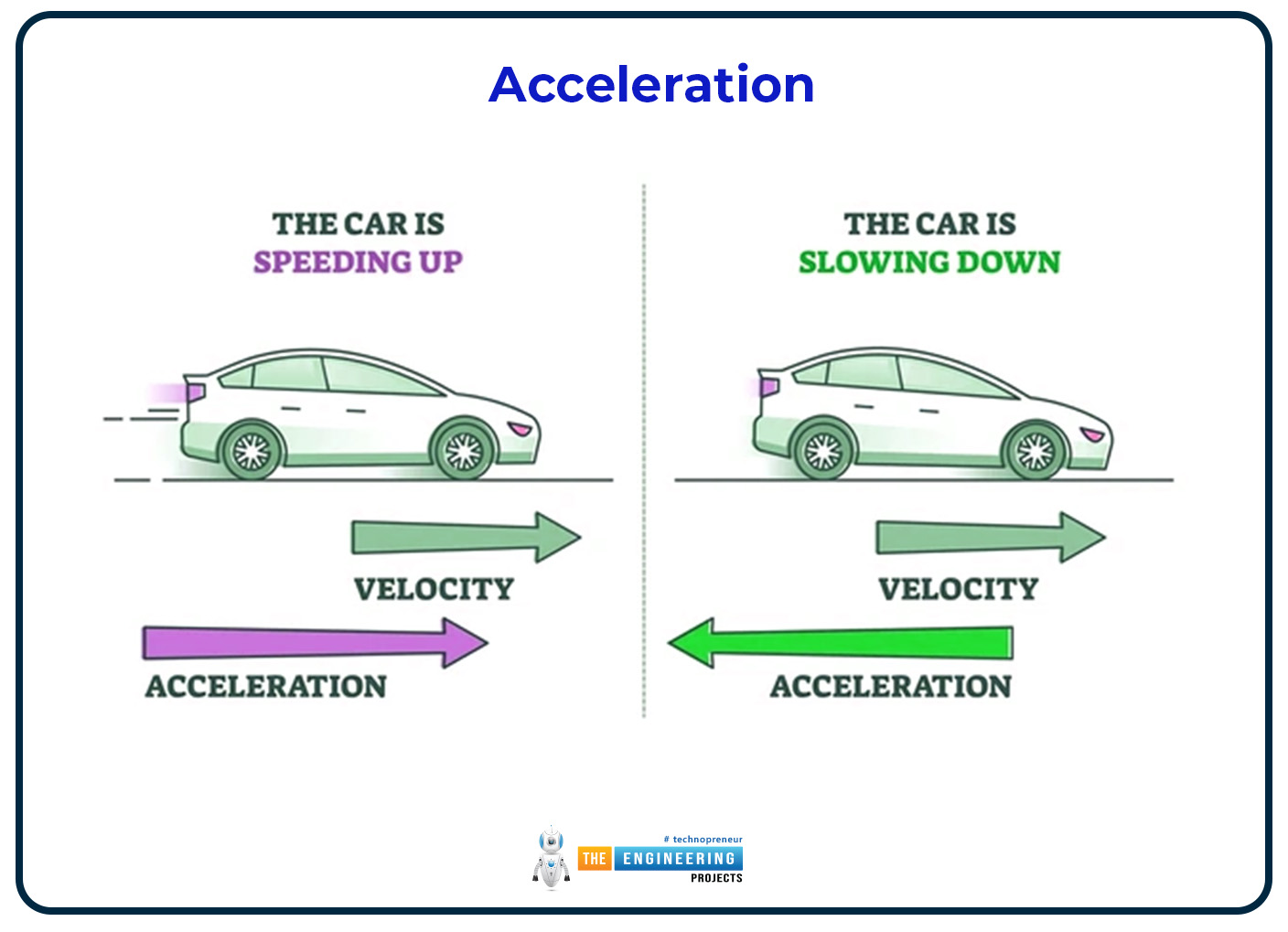
Acceleration (a):
The rate of an object's velocity changes, expressed in meters per second
Squares (m/s²). An object undergoes acceleration when its speed rises, falls, or changes direction.
Acceleration and force are two vector variables that are related by Newton's Second Law. It's crucial to realize that an object's acceleration will always point in the same direction as the total force applied to it since force and acceleration are vector numbers. Although the acceleration's magnitude varies with the object's mass, it is always proportionate to the force. The precise relationship between the vector's force and motion is provided by Newton's Second Law. Therefore, we can use this rule to quantitatively anticipate how an item will move given the forces acting against it.
Examples and Practical Applications:
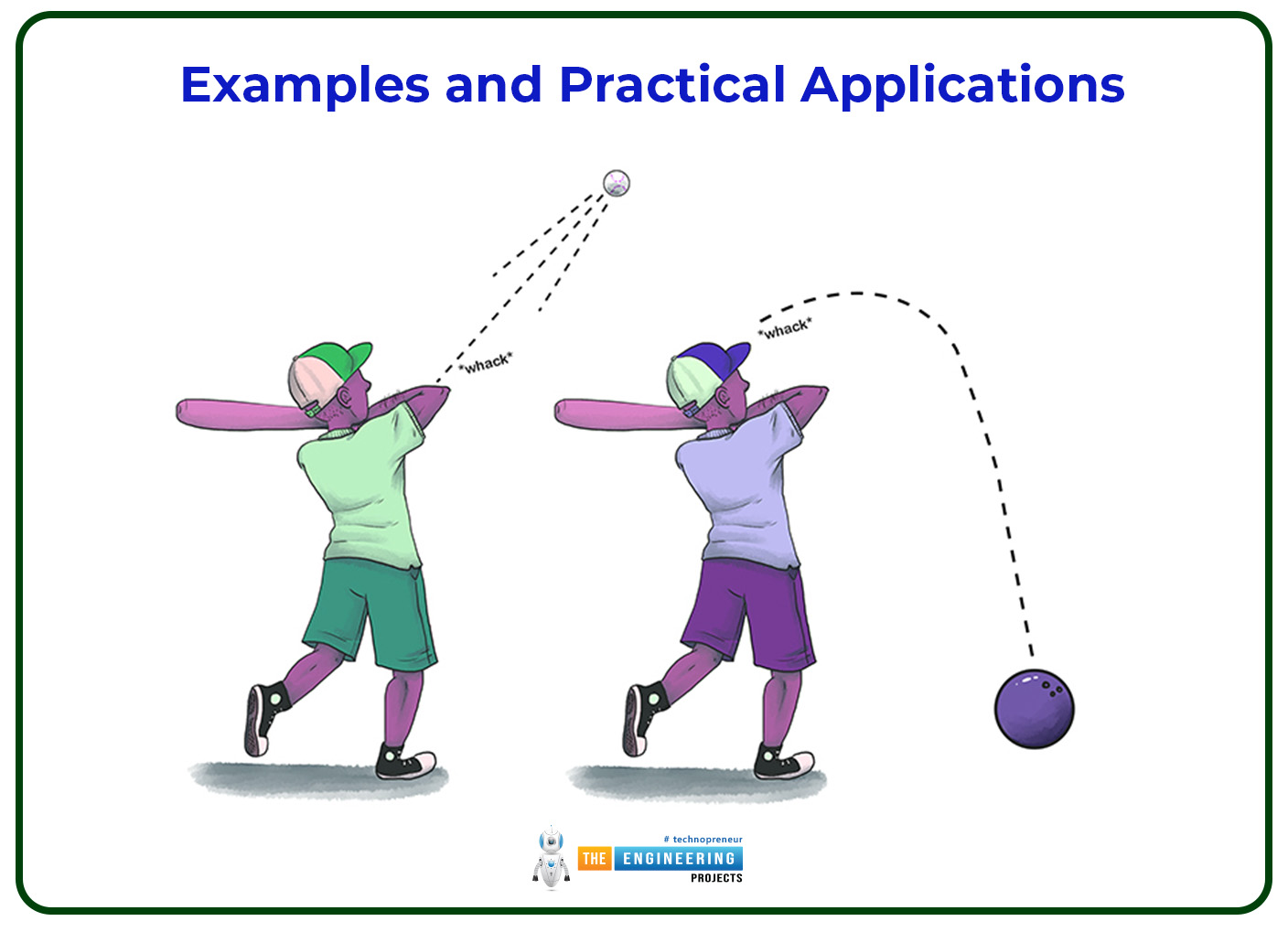
Examine the vehicle speeding down a road. The automobile moves forward due to the force produced by the engine. Newton's Second Law states that the mass of the vehicle and the engine's force determine how fast the automobile accelerates. With the same amount of force, a lighter automobile (less mass) accelerates quicker than a larger one.
Consider the kicking of a soccer ball as an additional illustration. The ball accelerates at a different pace depending on the force of the kick. The ball travels farther and quicker with a harder kick because it accelerates more quickly.
If two persons are walking and one of them weighs more than the other, the heavier person will go more slowly since their acceleration is larger. In a supermarket, pushing an empty cart is simpler than pushing one that is full, because greater mass calls for greater acceleration.
Implications in Engineering and Technology:
The Second Law of Newton is essential to several engineering specialties. This equation makes it easier for engineers to calculate the forces needed for desired accelerations in the construction of automobiles, allowing them to create strong engines and effective braking systems. Determining the force required by rockets to overcome Earth's gravity and reach space is critical in the field of aerospace engineering.
Newton's Third Law ( Action and Reaction):
An important idea that describes how two objects interact is Newton's Third Law of Motion. It asserts that there is an equal and opposite response to every action. This indicates that forces always exist in pairs: whenever one item applies a force to another, the other object responds by applying an equal and opposite force to the first object.
It's likely widely understood that a ball exerts force on a wall when it is thrown against it. Similar to how the ball bounces off the wall, the wall exerts force on the ball. Similarly, the Earth's gravitational attraction pulls you down. You might not be aware of this, but you are also applying the same amount of force on the Earth as well. This astounding truth results from Newton's third law.
According to Newton's Third Law, if object A applies a force to object B, object B must apply a force to object A in an opposing direction and of equal magnitude. This law represents a certain symmetry in the natural world: forces always come in pairs, and one body can't put force on another without receiving the force.
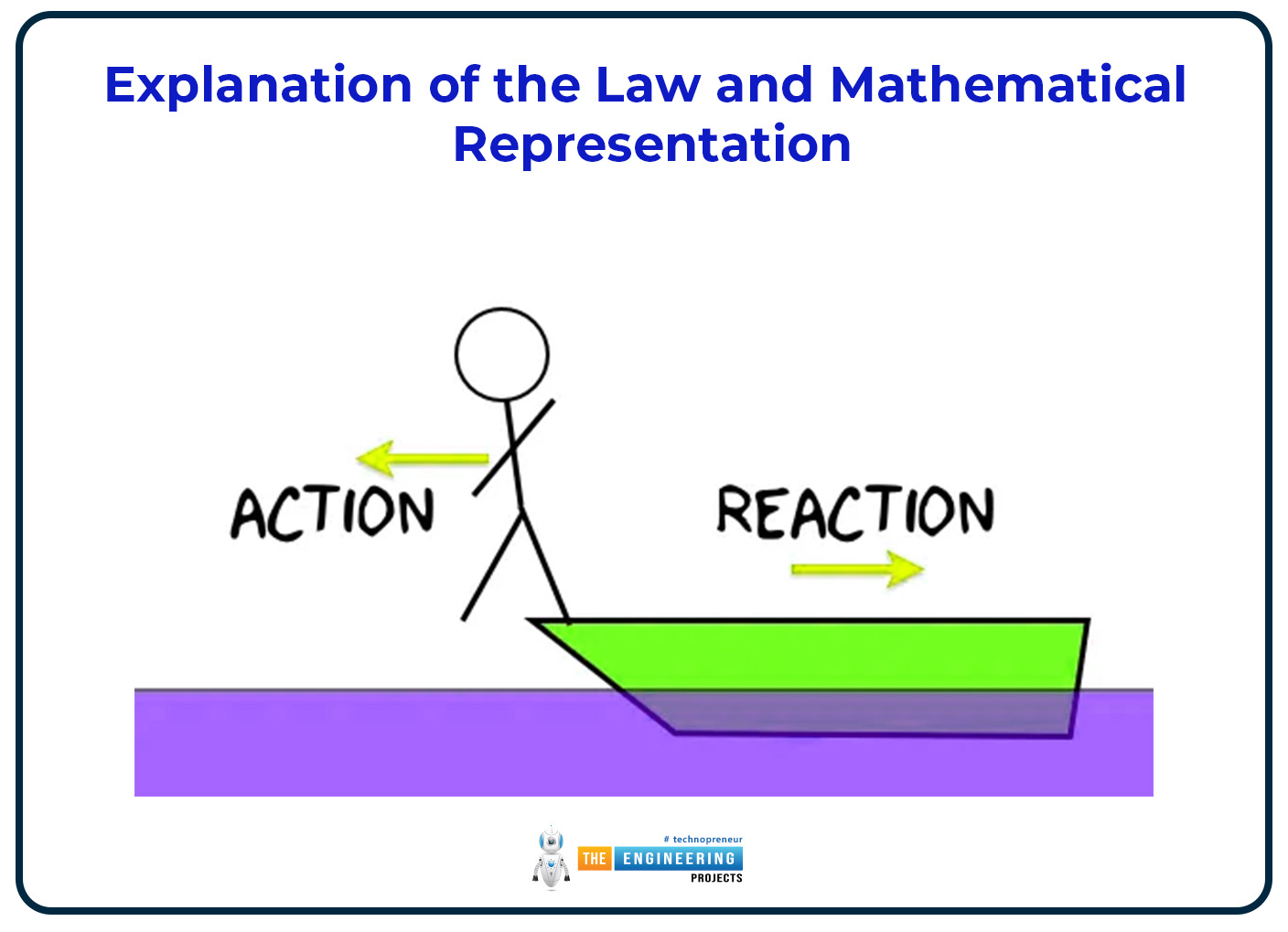
Explanation of the Law and Mathematical Representation:
It's likely widely understood that a ball exerts force on a wall when it is thrown against it. Similar to how the ball bounces off the wall, the wall exerts force on the ball. Similarly, the Earth's gravitational attraction pulls you down. You might not be aware of this, but you are also applying the same amount of force on the Earth as well. This astounding truth results from Newton's third law.
According to Newton's Third Law, if object A applies a force to object B, object B must apply a force to object A in an opposing direction and of equal magnitude. This law represents a certain symmetry in the natural world: forces always come in pairs, and one body can't put force on another without receiving the force.
The law can be mathematically represented as:
FAB = - FBA
In this case, object A's force on object B is denoted by FAB, and object B's force on object A by FBA. These forces are acting in opposition to one another, as indicated by the negative sign. This equation ensures that the entire momentum of a closed system is preserved by highlighting the mutual and simultaneous nature of forces.
Common Examples in Nature and Technology:
Numerous natural events and technology applications demonstrate Newton's Third Law. When you walk, for instance, your foot pushes back against the ground (action), and the earth pushes your foot forward (reaction), which moves you ahead. Another instance is when you push water backward with your hands and feet when swimming; this movement causes the water to push you forward in response.
This rule is essential to the operation of rockets in technology. Space travel is made possible by the response of a rocket's engines expelling gas, which propels the rocket in the opposite direction. Similar to this, in aviation, the process of pushing air downward results in the lift force produced by an aircraft's wings, whilst the reaction force raises the aircraft higher.
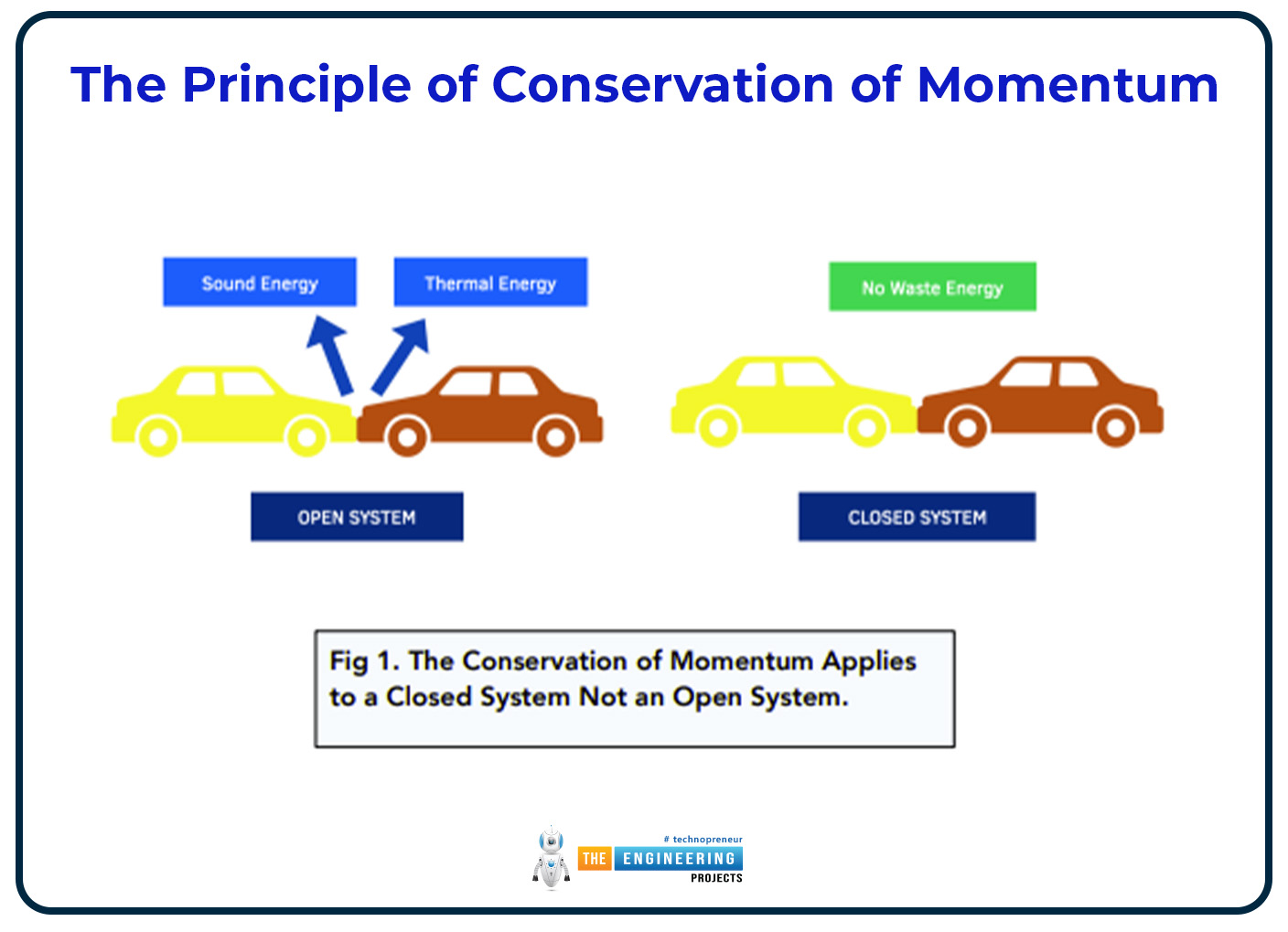
The Principle of Conservation of Momentum:
The concept of conservation of momentum, which asserts that the total momentum remains constant in a closed system in the absence of external forces, is based on Newton's Third Law. This idea is fundamental to several disciplines, including engineering, physics, and astronomy. For instance, the system's overall momentum before and after a collision stays constant, making precise predictions about the results of these interactions possible for scientists and engineers.
To grasp to create safe and effective systems in manufacturing, transportation, and even sports—where managing and transferring momentum may have a big impact on both performance and safety—it is essential to comprehend this idea.
Common Misconceptions About Newton's Laws:
Newton's Laws of Motion are core to physics, however, they are often misinterpreted or oversimplified. Addressing these misunderstandings is necessary for a comprehensive understanding of how the physical world functions.
Clarifying Misunderstandings and Myths:
"An object at rest will stay at rest forever unless acted upon by a force" is a frequent misperception. Newton's First Law does not suggest that things "prefer" to remain at rest; rather, it just indicates that an item will not alter its state of motion without a force. This rule also holds for moving objects, which, absent a force that causes them to halt or change direction, will continue to move in a straight path at an unchanged speed.
The notion that "force is needed to keep an object moving" is another common misconception. Actually, in a frictionless environment, Newton's First Law states that no force is needed to keep an item moving. Continuous force is only required to keep an item moving at a constant speed when external forces like air resistance or friction impinge on it.
One popular misconception regarding Newton's Third Law is that "if forces are equal and opposite, they cancel each other out." This is untrue since the forces operate on distinct things rather than canceling each other out. For instance, when you push against a wall, the wall pushes back against you in return. However, since these pressures occur on distinct bodies, they do not cancel each other out.
Real-World Scenarios vs. Ideal Conditions:
Conditions in the actual world are rarely the same as the idealized ones mentioned in physics principles. For example, friction is almost always present and needs to be taken into account when using Newton's Laws. Although these laws are taught under the assumptions of frictionless surfaces and perfectly elastic collisions, real-world situations include a variety of factors, including air resistance, friction, and material flaws, which can change the results that the laws predict.
Newton's Laws may be applied in predicting the typical outcome of auto accidents, providing a demonstration of this. For a thorough study, though, additional variables including the state of the roads, the design of the car, and safety measures like crumple zones and airbags must be taken into account. These variables alter the perception of forces and the transfer of momentum, highlighting the distinction between applied, real-world physics and theoretical physics.
Comprehending these fallacies and practical complexities contributes to clarifying the actual essence of Newton's Laws and guarantees their more precise implementation in scholarly research and real-world situations.
The Impact of Newton's Laws on Modern Science:
Newton's Laws of Motion are not just historical landmarks in science; they continue to be fundamental to our understanding and technological advancements today. These laws have profoundly shaped the fields of classical mechanics, engineering, physics, and beyond.
Influence on Classical Mechanics:
Newton's Laws form the foundation of classical mechanics, a branch of physics concerned with the motion of objects and the forces acting upon them. These laws offer a methodical approach to examining and forecasting the behavior of physical systems, from the orbits of celestial bodies to the operation of machinery and buildings. The precision and lucidity of Newtonian mechanics have shown to be indispensable in the understanding of common physical phenomena, particularly those involving much slower speeds and smaller distances than those covered by relativity or quantum mechanics.
Newton's Laws are a practical way to solve force and motion problems in classical mechanics. They can be used to calculate trajectories, design stable structures, and optimize mechanical systems. The predictive power of these laws has not only aided in the development of engineering and technology but also served as a foundation for investigating more intricate scientific theories.
Newtonian mechanics is still very useful and practical in most common circumstances, even if contemporary physics has brought new paradigms like Einstein's theory of relativity and quantum mechanics, which deal with extreme conditions involving high velocities or subatomic particles. This constant applicability highlights the essential part that Newton's Laws play in our continuing investigation and comprehension of the physical cosmos.
Foundations for Engineering, Physics, and Technology:
Newton's Laws are fundamental to engineering design and analysis of equipment, vehicles, and structures. For example, knowledge of force and motion aids in the construction of effective engines, sturdy bridges, and automobile safety equipment like airbags and seat belts. These physics rules form the cornerstone of more intricate theories and are essential to fields like electromagnetic, thermodynamics, and fluid dynamics.
Newton's discoveries have much to do with technology as well. His rules' guiding ideas have paved the way for the advancement of common technology, including advanced robots and home appliances. They are also essential to the creation of contemporary infrastructure, including communication and transportation networks.
Legacy in Modern Research and Space Exploration:
Newton's Laws continue to influence contemporary science and space exploration. These laws aid in the study of celestial motions in astrophysics, such as planet orbits and the dynamics of stars and galaxies. For space missions, the concepts are essential for computing trajectories, launch windows, and orbital maneuvers.
The concept of action and response is explained by Newton's Third Law, which is especially significant for rocket propulsion. According to this theory, spacecraft may move in a vacuum by releasing gas in one direction, which generates thrust in the other direction. Numerous space missions, including those to the Moon, Mars, and beyond, have relied heavily on this.
All things considered, Newton's Laws have not only given rise to a solid basis for scientific research and technological development, but they also serve as a source of inspiration and support for modern scientists and engineers. They are still important now just as they were centuries ago because of their effect on almost every facet of contemporary science and technology.
Conclusion:
Newton's Laws of Movement figured out in the 17th century, stay urgent in grasping the actual world and its basic standards. These regulations, embodying the ideas of inertia, power, and activity response, have given an establishment to traditional mechanics and keep on illuminating present-day science and technology.
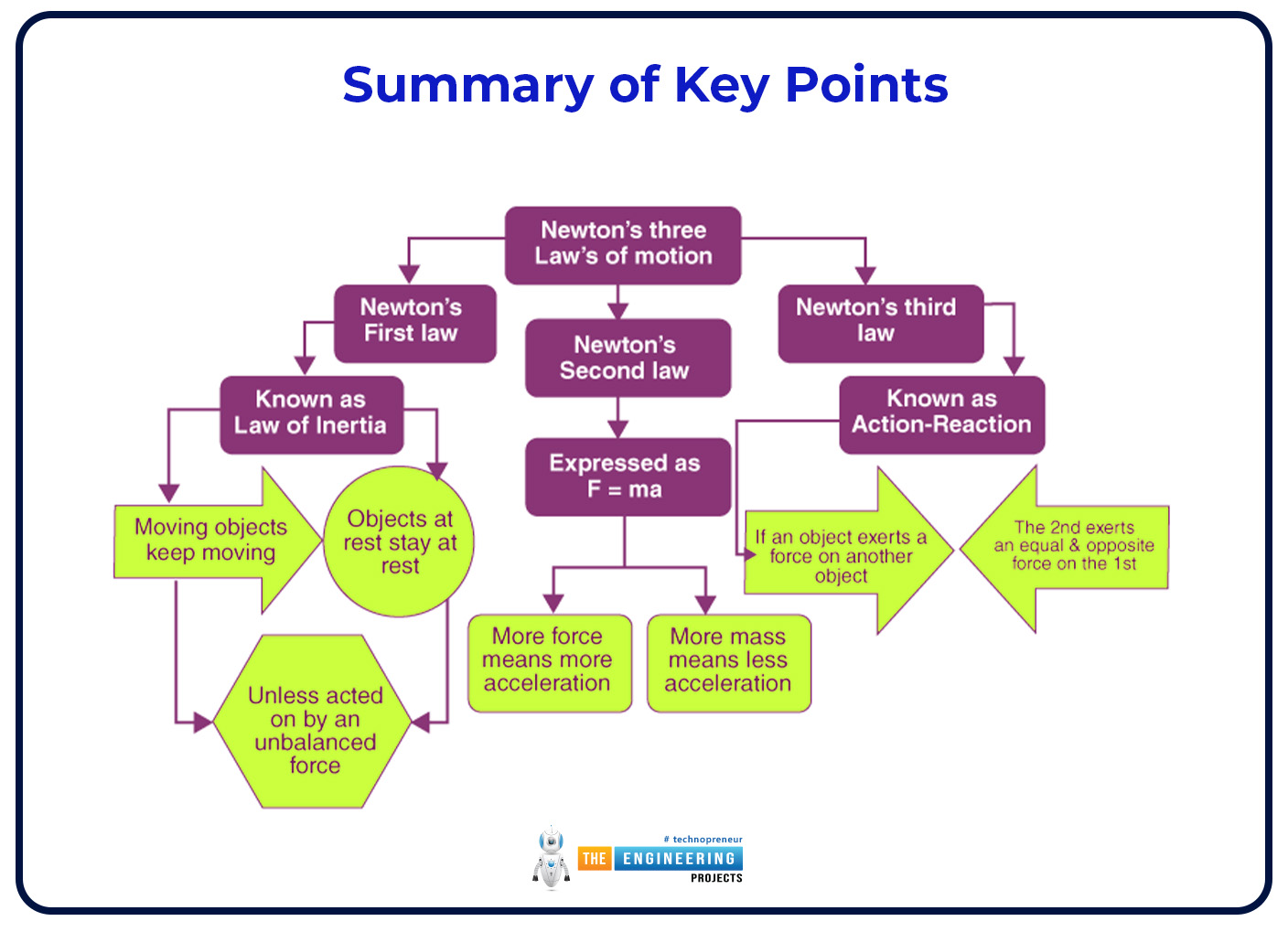
Summary of Key Points:
An object will remain in its condition of rest or uniform motion until it is acted upon by an external force, according to Newton's First Law, the Law of Inertia. The connection between force, mass, and acceleration is quantitatively described by the Second Law and is expressed as follows: F = ma. Reiterating the idea that "for every action, there is an equal and opposite reaction," the Third Law emphasizes the reciprocal pressures that are felt by interacting objects.
These ideas are not only theoretical; they have real-world applications in several disciplines, such as technology, engineering, and space exploration. Their tremendous influence on both our everyday lives and the larger cosmos may be seen in the development of transportation systems, cutting-edge technology, and space exploration.
The Continuing Relevance of Newton's Laws in Contemporary Science and Technology:
Newton's Laws are still important in modern science and technology because they shed light on how physical systems behave. They are essential to the design and analysis of anything from sophisticated aeronautical technology to commonplace machines. These principles continue to be a pillar of knowledge as we push the bounds of scientific discovery and technological advancement, directing study and advancement in disciplines as varied as robotics, astronomy, and mechanical engineering.
Newton's Laws continue to provide a solid foundation for comprehending and forecasting occurrences within their relevant range, even as we delve deeper into new areas of physics like relativity and quantum mechanics. The fact that these ideas are still relevant today proves how timeless they are and how important a part they have played in forming our perception of the world and the cosmos.