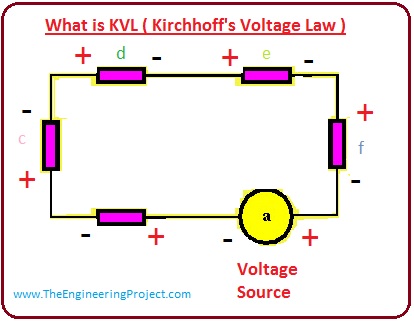
What is KVL, KVL working, KVL applications, KVL equations, KVL
Hello friends, I hope you all are doing great. In today’s tutorial, we will have a look at What is KVL ( Kirchhoff’s Voltage Law). KVL is an elementary law of electrical circuitry. In 1845, a German physicist Gustav Robert Kirchhoff gave two basic laws to solve electronic circuits. First one is KVL ( Kirchhoff’s Voltage Law ) and the second one is KCL ( Kirchhoff’s Current Law ). These Kirchhoff's laws are successors of Ohm’s Law which was given by George Ohm and followed by Maxwell equation which was given by James Maxwell. Both of these laws playing a very important role in solving different circuits in engineering projects. These rules are also useful for frequency and time calculations. Kirchhoff’s laws are not only applicable to DC circuitry, but also works for the AC circuits, when the electromagnetic radiation has large frequency values. In simple words, KVL says that the sum of voltages in an enclosed loop circuit is always equal to zero. By using this law we can easily find different parameters of a circuit like resistance, current or voltage quite easily. In today’s post, we will have a look at its introduction, working, applications and other parameters. So, let’s get started with What is KVL ( Kirchhoff’s Voltage Law ).

What is KVL ( Kirchhoff’s Voltage Law )

  • KVL ( Kirchhoff’s Voltage Law ), also known as the second rule of Kirchhoff’s, explains that the sum of voltages in an enclosed circuitry is always equal to 0.
  • KVL applied for voltage measurement in circuits. To explain it we discuss given circuitry.
  • As you can see in a given circuit that the single voltage source is linked with the passive elements  (the electric element which does not produce power like a resistor), which have (b,c,d,e,f) voltage about them.
  • As all these elements are connected in series so there voltages values will be added.
  • If we apply KVL (Kirchhoff’s voltage law) which says voltage around the passive (the electric element which does not produce power, like a resistor) element in circuitry always equivalent and reverse to source voltage.
  • Therefore, the summation of the voltage changes across all the elements in circuitry is always equated to 0.

a+b+c+d+e+f=0

What is KVL, KVL working, KVL applications, KVL equations, KVL

 

What is Mesh Analysis

  • It is the method to helps us to find the current and voltage in any close-loop working with the KVL, by this analysis we can find values of current and voltage across any component of the loop on the circuit.
  • There are three steps to apply this mesh analysis. Which described here.
    • Allocate discrete current values to every enclosed circle of the network.
    • After that Apply Kirchoff voltage law about every enclosed circle of the system.
    • And resolve the resultant concurrent linear equations to find the value of current in the ring.

Example of Mesh Analysis

Now we practically discuss the Mesh Analysis by the given example.
  • Let's suppose that we have a given circuit diagram which has two loops and we have to apply mesh rule on this circuit.
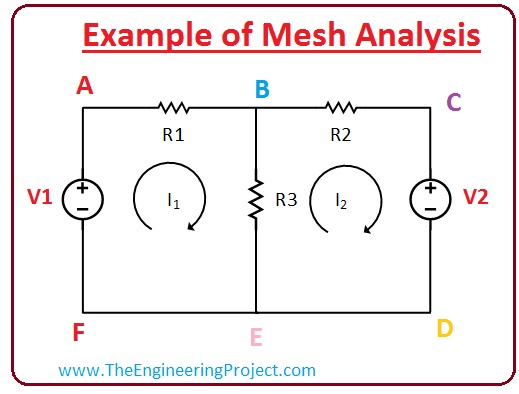
    What is KVL, KVL working, KVL applications, KVL equations, KVL
  • The values of the elements of this circuit which we know are given below.
  • (R1)= (5 ohms)
  • (R2) = (6 Ohm)
  • (R­­3)= (10 ohms)
  • (V1) = (12 volts)
  • (V2)= (8 volts)
  • To apply mesh rule on this circuit, first of all, we recognize the direction of the current flowing in these two loops.
  • In the first loop which is (ABEF) the direction of current is clock-wise and it is represented as (I1).
  • In the second loop which is (BCDE) the direction of current (I2) is also clockwise.
  • Now applying kVl to write the equation for both of these two loops.

(V1)= (R1I1)+ R3(I1 - I2)

  • This equation can also be written as
 

(V1)= (R1 +R3)I1-R3I2 – (A)

  • Now if we apply KVL on loop 2 then we have this equation.

(V2) = (R2I2)  + (R3)(I2-I1)

  • It can also be written as

(V2) = (R2+R3)I2 –(R3I1) – (B)

  • Now we will put the values of given parameters of circuit and find the value of the unknown parameter.

(12) = (5+10)(I1)- (10)I2

12= (15I1)- (10I2) –(C)

  • When we put value in equation B it will become

(8)= (6+10)(I2)- (10)(I1)

8=16 (I2)-10(I1) –(D)

  • By solving equation C and D we have.

I1= 1.94 A

I2=1.7 A

Example of KVL ( Kirchhoff’s Voltage Law )

  • In the given diagram, a circuit is drawn at which we have to apply KVL.
  • In this circuit, there are three loops which are labeled in the circuit by no 1, 2, 3.
  • We will apply KVL on these three loops one by one and will get correspondent equations.
  • When we apply KVL to the first loop we get this equation.

V1= (I1 x R1) + R3(I1+I2)

10= (I1 x10) + 40(I1+I2)

10= 50 I1 + 40 I2

  • After applying KVL on the first loop we now apply it on the second loop then we get an equation for this loop.

V2= (I2 x R2) + R3(I1+I2)

20= (I2 x 20) + 40(I1+I2)

20 = 40 I1+ 60I2

  • After findng equations for loop first and second now we find the equation for the third loop.

V1-V2 = (I1 x R1) – (I2 x R2)

(10-20) = (10I1) – (20I2)

  • By solving equations of loop one and second we get the value of (I1) and (I2) which are mention below.

I1= -0.143 A

I2= +0.429 A

  • By using the value of I1 and I2 now we find the value of current I3.

(I3 = I1 + I2)

  • Putting the value of I1 and I2 we get current at resistance (R3).

I3 = -0.143 + 0.429 = 0.286 A

  • I3 is the current which is passing through the resistance (R3), we can also find the value of voltage across this resistance by using I3.

V3= (0.286 x 40) = 11.44 V

What is KVL, KVL working, KVL applications, KVL equations, KVL

Applications of KVL Law

  • These are some important applications of KVL law.
    • Kirchhoff’s laws are used to measure the unknown standards such as current (I), Voltage (V),  also the direction of moving current in the circuit.
    • This rule is applicable to every circuit but it is very fruitful to solve complicated circuitries.
    • This law also helps us to observe the transferal of power in the circuit.
This article was about KVL law, I tried my best to explain to you in the simplest way if you have any question about it ask in comments. I will solve your problems and will guide you comprehensively. Thanks for reading. Take care until the next tutorial.