What is Maximum Power Transfer Theorem
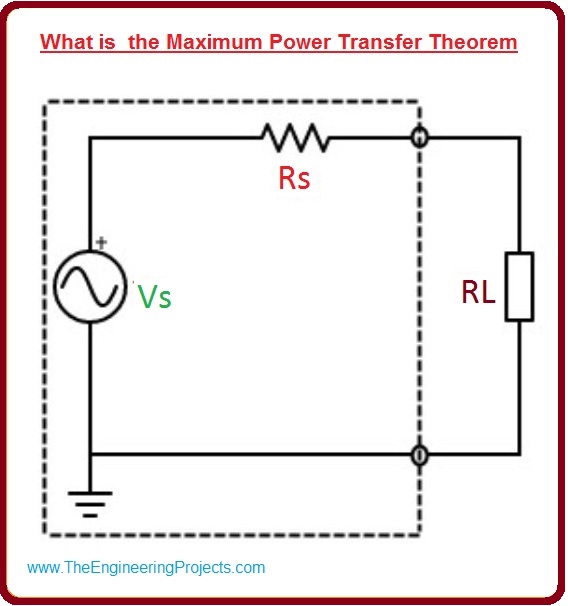
- Maximum Power Transfer Theorem says that the maximum power will be transferred to the load from the source if the resistance load will be equal to the interior resistance of the source.
- The main thing you should keep in mind that this theorem is related to the power measurement, not the efficiency.
- We can understand this point by an example, let’s suppose that if we increase the resistance of the output then the resistance of the source, due to this efficiency will increase, but the power at out will be less because the net resistance of the circuitry has increased.
- If we decrease the output resistance value then supply, due to this mostly power will be wasted in the source, though the net power loss is large, due to less value of total resistance, it causes the less power loss at the output.
- This theorem also helps us to find the value of resistance at the load so that maximum power can be sent to the load from the input.
- Maximum power theorem also works for the AC circuitries which has impedances and says that power will be transferred to the output if its impudence is identical to the impedance of the input supply.
- You should keep in mind that efficiency is the important factor in the power system, while power transfer is the main fact for communication techniques.

Steps To Solve Maximum Power Transfer Theorem
- These are some steps we should follow to use the maximum power theorem.
- First of all, eliminate the load resistor (RL) from the circuitry.
- Calculate the Thevenin resistor (RTH) of the source system observing from the open terminals.
- Rendering to Thevenin theorem, (RTH) is the load/output resistor of the system which means RL is equivalent to the RTH which permits extreme power transmission.
- Maximum Power Transmission is intended by the given equation.
(Pmax) = V2TH / 4 RTH
Example of Maximum power Transformer
- Now apply power transformer theorem practically on a given circuit diagram. For this purpose, we will apply practically above described steps of this theorem.
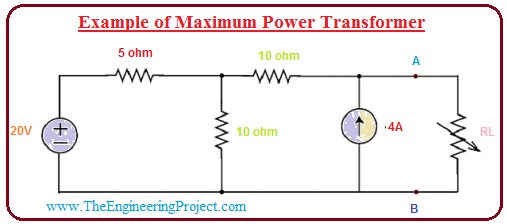
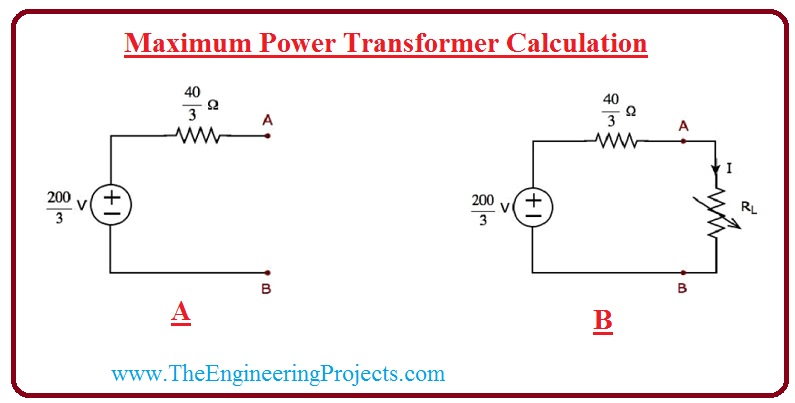
- First of all, you have to applied Thevenin theorem on lefts part of point A and B to find the Thevenin circuit which is shown is given diagram.
- In the specified figure we can get that the value of Thevenin voltage is VTH = 200/3V, and the value of the Thevenin resistor is Rth = 40/3.
- Swap the portion of the circuitry, which is left-side of point A and B of the assumed circuitry with the Thevenin’s correspondent circuitry.
- The subsequent circuitry denoted in figure as B.
- Now we calculate the extreme power which will be transported to the load resistance (RL) by given resulting formulation.
PL, Max =VTh2 / 4RTh
- By putting the value of Vth and Rth can find the value of a power transformer.
PL, Max = 250/ 3 W
Applications of Maximum Power Transfer Theorem
- This formula is permanently required in a communicating scheme. For example, in a public addressing scheme, the circuitry is adjusted for higher power transmission with a creation speaker equal to the loudspeaker. When the output and input have coordinated then it has the equivalent resistor(R).
- In-vehicle engines, the power communicated to the motor starting element of the vehicle will be contingent on the active resistor (R) of the motor and the batteries internal resistance (R). When the 2 resistors are equal, then the higher power will be communicated to the motor to start the engine.
Limitations of Maximum Power Transfer Theorem
- These the main limitations of the maximum power transfer theorem.
- The efficiency of this theorem is fifty percent so it is not useful for such circuits where efficiency is to be measured.
- This theorem works for all circuitries but device prepared according to it will have less efficiency. The presence of this factor is still used for speakers and receivers where power use is small and main concern is efficiency.