Resistors in Parallel Combination
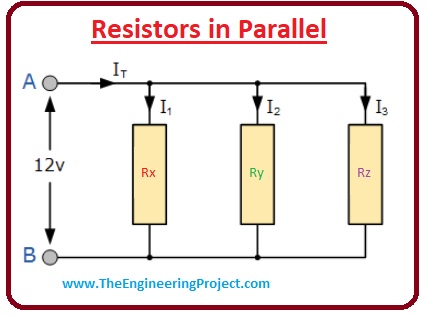
- In electrical circuitries, the resistances are parallel connected if their both endpoints are connected with other resistance or resistances endpoints.
- As in series resistance circuitry, there is one path for the current to flow but in the parallel circuitry, there are many paths for the current. Due to this parallel circuitries are also recognized as current divider circuitry.
- As there are numerous ways for the current in parallel circuitry, so different current will flow across every part of the circuitry. The voltage will be alike to every resistance of circuitry.
- In given below circuitry there are 3 resistances Rx, Ry, Rz, the voltage each of them will be the same.
VRx =VRy =VRz= 12V
- The method to find the equivalent resistance is to just add all series resistance in the circuitry, but in parallel connected resistances we add reciprocal of each resistance for equivalent resistance.
1/Rt = 1/Ra + 1/Rb +1/Rc .....1/Rn

Currents in a Parallel Resistor Circuit
- The net current passing through the parallel resistances circuitry is equivalent to the summation of the currents moving through every resistance of the circuitry.
- But the current across every branch of the circuitry will not be similar, in conclusion, every resistance of the circuitry's branch tell about the current flowing through that branch.
- For instance, as the voltage across every parallel resistor similar and due to different values of the resistance the current will not be alike.
- Let's make a circuitry that has 2 parallel resistances, it is shown in the given figure.
- The current passing through every resistance is IRx and IRy if we apply Kirchoff current law to this circuitry than we have.
It =IRx +IRy
- If we apply ohm law to both resistance than we can find the current passing through them.
IRx = V/Rx= 12/20= 0.6 ampere
IRy =V/Ry= 12/47=0.255 amperes
- So the total current will be.
It= 0.6 + 0.255= 0.855 amperes
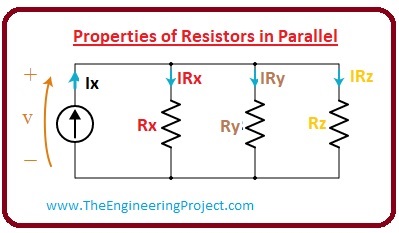
Properties of Resistors in Parallel
- In the given diagram a parallel resistance circuitry is shown that has 3 resistances Rx, Ry, Rz in parallel and one current source.
- The current Ix is flowing from the source to 3 resistances of the circuitry and will divide into three different paths.
- If we apply ohm's law to this circuitry than we have this expression.
Ix = IRx? + IRy? + IRz
- The voltage across every resistance will be.
VRx = (IRx) . (Rx)
VRy = (IRy) . (Ry)
VRz = (IRz) . (Rz)
- Now use these voltage value of every resistances and find the current flowing them.
IRx = VRx/Rx
IRy = VRy/Ry
IRz = VRz/Rz
- If we add these 3 current the resultant value will be equal to the current source.
Ohm‘s Law and Parallel Resistors
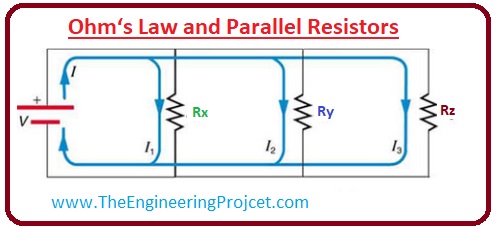
- To relate ohm's law and parallel combination of the resistor we take an example of the circuitry that the 3 resistors connected in parallel and voltage source are connected with them.
- The voltage across every resistance is equal to the voltage source. If we apply ohm's law the current across every resistance will be.
I1 =(V)/(Rx)
I2=(V)/(Ry)
I3= (V)/(Rz)
- According to charge conservation principle, the total current flowing in the circuitry will be equal to the current passing through these three resistances.
It = (I1 + I2 +I3)
- If we put the values of currents flowing in the 3 resistance then we have.
I = (V)/(Rx) + (V)/(Ry) + (V)/(Rz)
I =V (1/Rx + 1/Ry + 1/Rz)
- From this relation, we can conclude that the total resistance in parallel circuitry is equivalent to the summation of the inverse of every resistor.
- So, equivalent resistance in parallel circuitry is.
Rn = 1/Rx + 1/Ry + 1/Rz +.........+1/Rn
Applications of the Parallel Resistance Circuit
- These are some applications of the parallel resistance circuits.
- Almost every house on this earth uses a parallel combination for electric wiring, as we can on-off and appliances of our home without removing all devices from the circuitry.
- In case of any short circuit occurs at one device or it damage due to some electrical faults, we will off circuit to that particular device not the complete circuitry for fault removal.
- Parallel circuitries are not used only in a home is also used in transmission and distribution of the power to large buildings and different areas.
- Nowadays our grid stations are designed according to parallel circuitries combinations when the circuit of the feeder is trip, other feeders in the grid continue their working and deliver power to the load.
Parallel Resistance Calculator
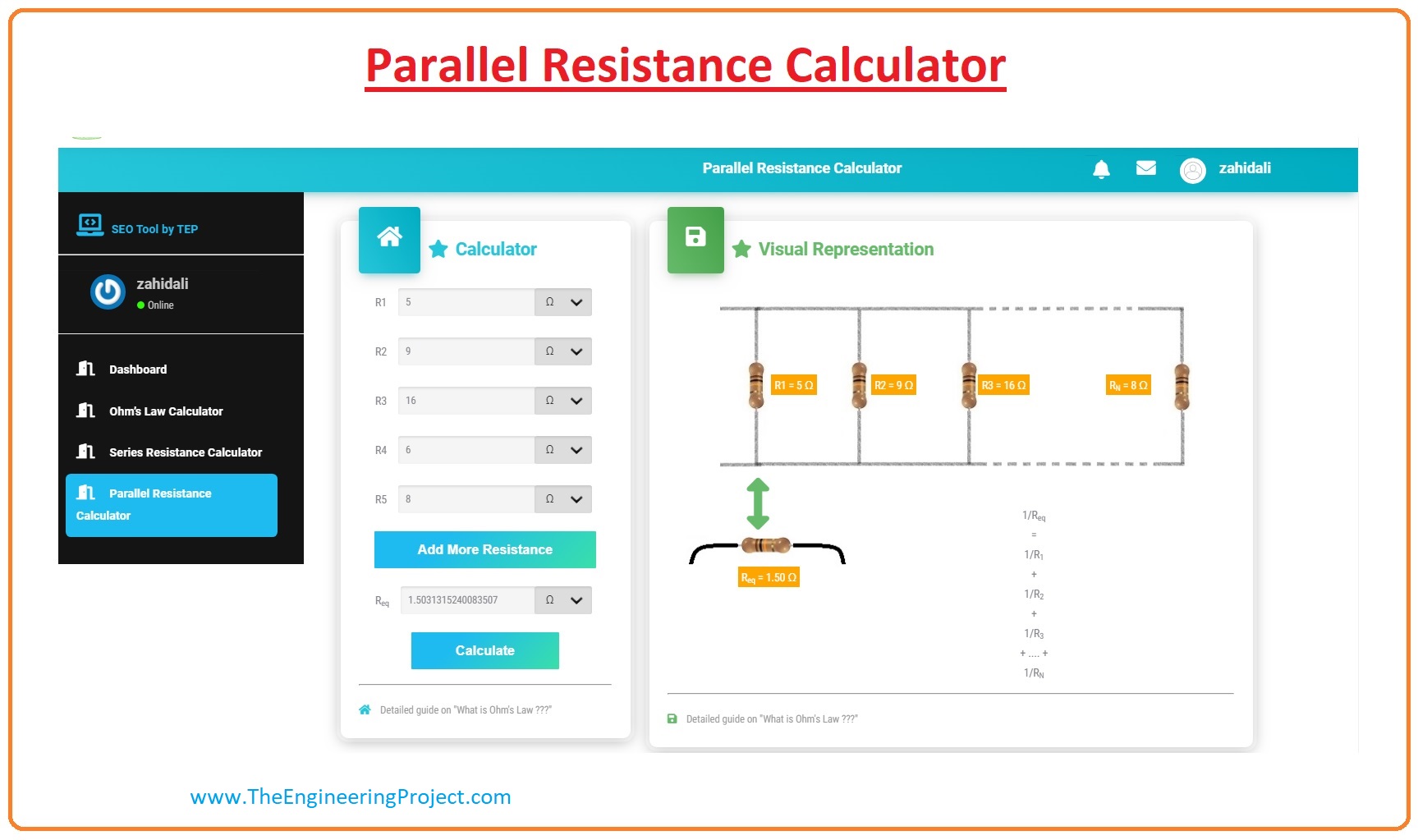
- As we discussed our Parallel Resistance Calculator now we discuss how you can use it for solving your circuitries.
- You can see in the given figure parallel resistance calculator, there are 2 portions of this calculators first is on the left side where you can add values of your circuits resistances and on right side physical representation of circuitry is shown.
- You can see in the given diagram, I have put different five values in the value box and get equivalent resistance of the circuitry. If your circuitry has large no of resistances you can add more resistance values by Add More Resistance option. You can also take values in kilo-ohm and mega-ohm.



 Tutorials
Tutorials zahidali
zahidali 0 Comments
0 Comments

















