Hi everyone, I hope you are doing well. Today in this post we can discuss significant figures. Significant figures can be evolved and traced a few hundred years ago and they can be developed from time to time according to the precise calculations that can be done in mathematics and modern science and technology.
The origin of significant figures can be traced to ancient times in Greece, Egypt, or many other countries where they can be used as Significant figures in calculations or mathematics. With time these significant figures can be used by astronomers, mathematicians, and scientists as well. To measure accurate and precise measurements they can use significant figures with scientific notation. In modern physics and mathematics, significant figures can be used essentially.
Now we can start our detailed discussion about significant figures and their definition, rules, examples, and problems in detail.
What are significant figures?
Details of significant figures are given below:
Definition:
Significant figures can be defined as:
"In the number or calculated value the specific digits which provide precision and accuracy and also impart and convey the necessity of digits in the calculated measurement."
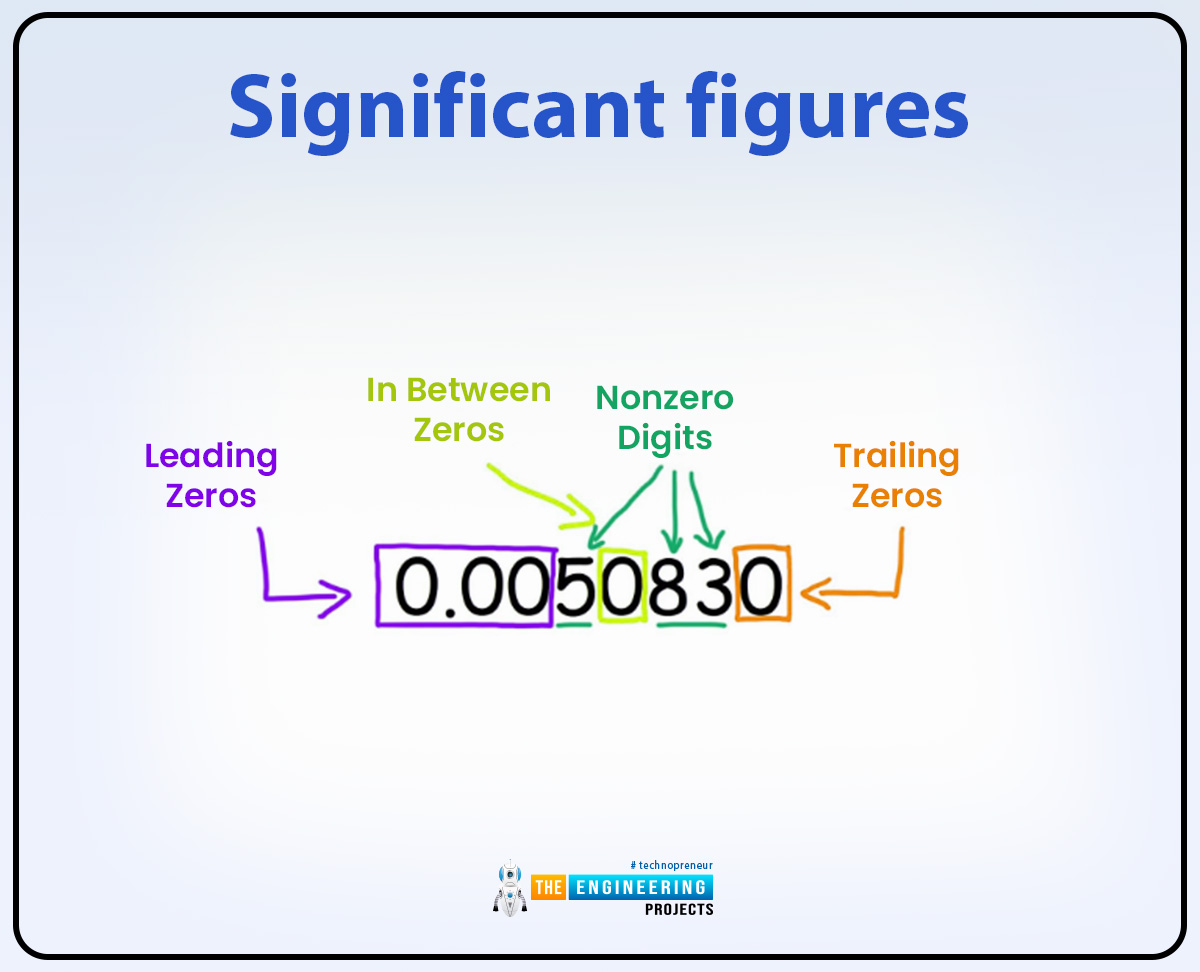
Significant figures include the zero or the nonzero digits. Significant figures are also known as significant digits and sig figs. When we make measurements or calculate the measurement such as when we measure length, pressure, and volume and the measured value is large then we can use significant or scientific notation method. or the most capable digits are estimated and called significant figures.
Such as if we measure the volume of a cylinder and the measurement is approximately equal to 3.97L and the uncertainty is approximately equals to 0.04L. The actual volume of this cylinder is approximately between 3.93L and 1.01L, but we can't know the certain digits in this measurement completely. But all of these three figures are called significant figures.
Additionally, the value 345.0 has only 3 significant figures 3,4, and 5 the o digit is not termed as a significant figure because it is only a placeholder.

Types of digits:
Some digits are not to be considered as a significant figure. So the types of digits that can't be considered significant figures are given below:
Spurious
Leading zero
Trailing zero
Trailing Zero:
The zero can only be present in the value or measurement as a placeholder. For example 1800 the last two zeros were only a placeholder but we can write the scientific notation we can raise the power of ten but in significant value, we only estimate and choose the figures that can provide accurate and precise measurement.
Leading zero:
The zero which can be present at the start of measurement and the value is known as leading zero. For instance, 00367 the first two zeros (00) known as leading zero and it can’t be a significant figure in this value 3,6, and 7 are the significant figures. Another example is 0.00456089 in this value the leading zero is not a significant figure but the zero which is present in between the digits like 6,0,8 and 9 is referred to as a significant figure.
Spurious:
Spurious digits are those when we do calculations on the instruments then the high-resolution measurement results precisions and the accuracy digits are known as spurious digits.
Another example is if the zero is present in the value after the decimal it can be considered a significant figure like 12.00 then these two zeros are also significant figures and in this value, the total no of significant figures is 4 but if the decimal is not present like 12300 then the last two zero is not considered as significant figure and in this value, the total significant digits are 5. After the decimal point, the zero is also considered as the significant figure for example 1.000 the last trailing zeros are also the significant figures and the total significant figures in this value is 4. But if the decimal is not present like 1000 then this value has only one significant figure and trailing zeros are only a placeholder.

Examples of significant figures:
Some examples of significant figures are given below:
123790: All digits in this value are known as significant figures.
0.0056:in these digits the leading zero is not a significant figure the last two 5,6 are significant figures.
34986097: all digits are significant figures and the zero which is present inside them like 6,0,9,7 all are significant figures.
1001: all digits are the significant figures.
Rules for determining Significant figures:
To identify the significant figures from the measurement and for the value, there are some rules. The rules that can help to identify the significant figures are given below:
Non-zero digits in the measurement are to be significant
Between the two significant digits, the zero is also a significant figure.
Starting, leading zeros are not a significant figure.
Zero after the decimal point on the right side can also be a significant figure.
Trailing zero without the decimal point is not significant.
Nonzero digits in the measurement are significant figures:
All non-zero digits in the measurement or the value are significant figures some examples are given below:
9144 all the digits in this value are significant. So the total significant digits is 4.
1.5678 all the digits after decimal or before decimal are considered as significant figures and the total significant digits in it is 5.
568.9 these all digits are significant figures.
Between the two significant digits, zero is also considered a significant digit:
The digit zero is not to be considered to be significant but in between the two the significant digit zero also becomes a significant digit some examples are given below:
10054 in this value all digits including zero are referred to as significant figures.
102.60809 these all digits are considered significant figures the zeros after the decimal point are also considered significant figures.
101.101 in this value all digits are also considered as the significant digits or figures.
Leading zero, and starting zero are not considered significant figures:
The starting or the leading zero is not considered to be a significant figure it can only considered as a placeholder some examples are given below:
000102 in this value last 3 digits 1,0and 2 are called significant but the starting three zeros are not considered to be significant but it is only placeholder or leading zeros.
0.065 the last two digits 6 and 5 are sig figs but the starting zero or zero after the decimal point is not considered a significant figure.
Trailing zero, zero after the decimal point is considered a significant figure:
The trailing zero, the zero on the right side after the decimal point can considered a significant figure. Some examples are given below:
1.89900 these all digits are considered to be significant digits. In this value, the digits 1,8,9,9,0,0 all are significant figures including the trailing zeros.
0.1200 in this value 4 digits are called significant figure 1,2,0 and 0 are significant figures which are trailing zeros but the first leading zero is not considered as the significant figure.
Trailing zero without a decimal point is considered a non-significant digit:
The trailing zeros without the decimal point are not considered as a significant figure. some examples are given below:
19900 the first 3 digits 1,9 and 9 are considered as the significant digits but the last trailing zeros are not to be considered as the significant figure.
1096800 in this value the first 5 digits are considered to be significant but the last trailing zeros are not a significant digit or a figure.
Rounding rules for significant figures:
The rounding-off technique can be used in mathematics in all calculations. In this technique the last digit if it is greater than 5 then it can be added to the previous number. for representing the rounding off number we can use n. To round the significant digit with n there are some rules which are given below:
In the measurement value if the last digit is greater or equal to the 5 then we can +1 inti the previous digit. For instance, 1.345 then after rounding the digit the new value is 1.35 and it has 3 significant figures now.
Another example is if we have 5 significant figures like 5.9867 then after rounding off the last digit the new value is 5.987 and they have only four digits in it.
Now if we have the last digit less than 5 then it can’t be added to the previous number some examples are given below:
1.563 the last digit is less than 5 so it can’t added 1 to the previous digit and the significant figure in this value is 4. Another example is that 67.91 has the 4 significant figures and they can’t be changed because the last digit value can’t be added.

Numerical value formula:
To calculate the numerical value of significant figures for nonzero significant figure x and for the precision and accuracy p we can use the formula which is given below:
10n. Round (x10n)
Where the n is equal to,
n=[log 10(x)]+1-p
Precision and accuracy in measurements:
In the measurements precision and accuracy, both are essential. Generally, we can use precision for the stability of the measurements with repeated values and the accuracy used for the closeness to the actual and accurate measurement of the thing and the object. but with time in modern technology and science, both precision and accuracy are termed for trueness or the most closeness exact value of the measurements. In the scientific community, the accuracy and precise measurement of the object is essential because without accuracy the measurements and problems become more complicated That is why accuracy and precision both are essential for measurements.

Addition and subtraction:
In addition and subtraction, the result of measurements can calculated with the same decimal point before and after the addition and subtraction for example:
12.56+ 0.5=13.1 they have the 3 significant figures in it another example is that
67.9+9 =76.9 and the significant figure in it is 3.
Multiplication and division:
The result that can be taken from measurement and the result after division and multiplication of values both have the same significant figures some examples are given below:
4.56 1.4 = 6.384 and we should rounded to 6.4 then they have 2 significant figures like before the division. another example is that 2.44 then it is equal to 9.6 they have also 2 significant digits like before the multiplication or division.
Certainty in significant figures:
In the measurement, certainty means that we confidently know the significant digit in the measurements. This known digit conveys and provides the precision of measurement and is also considered reliable because accuracy and precision are very essential in the measurements.
For example, if we can measure the length of an object with a ruler that has a millimeter marking and the measurement is equal to 24.87 then the digits 2,4,8, and 7 are certain because measurement tools can provide precise and accurate measurements.
Uncertainty in the significant figures:
Rather uncertainty in the significant figures means that which measurements we can take are not precise and accurate and we have doubts about them. When an unskilled person or limited measurement tool is used for measurement then chances of uncertainty increase because a skilled person can take accurate and precise measurements of the object and the high precision measurement tool is also needed.
For example, if we can measure the length and the measurement is 24.56 then the last digit 6 creates uncertainty because it can be rounded off and the original length can't be measured precisely and efficiently. So that's if we want to remove uncertainty then we again measure the length and then determine the significant figures in it.
Examples of significant figures:
Some examples of significant figures are given below:
406.62 all digits in this are significant figures and the total significant figures is 5.
0.00034 the last two digits are signification figures and the starting zeros are leading zeros.
12090 all are significant figures and the last zero is only a placeholder.
74.0 the zero after decimal is also a significant figure the total significant figure is 3.
67.08 in this all digits are significant figures and the total is 4.
These are some common examples of significant figures.
Practical problems and their solutions:
Some practical problems to understand the significant figures are given below:
Problem no 1: Identify the significant figurae:
Identify the significant figures in the given problems:
7696
0.0074
690.00
60.09
74.0
Solution:
Solutions to these problems are given below:
All 4 digits are significant figures.
Leading zeros are not significant digits but the last 2 digits 7 and 4 are significant.
All 5 digits including zero after decimal are also considered significant digits.
6,0,0 and 9 all digits are considered significant figures.
7 and 4 including trailing zero after the decimal are also considered significant figures.
Problem no 2: Calculations for significant figures:
The calculation to determine or calculate the significant figures some problems are given below:
26.7+ 8.1
62.4 0.04
2.4+ 9.2
58.0+ 4.5
0.056/0.0007
Solutions:
The solution to these problems is given below:
34.8 in this value 3, 4, and 8 are significant figures.
2.496 in this value 4 significant digits are present.
11.6 in this solution all digits are considered significant figures.
62.5 in this solution of a problem all digits are significant digits.
80 are the solution and both are significant figures.
Problem no 3: Combined operations:
To determine the significant figures, perform the following operations:
(2.7+ 4) 7.9
(5.6 8.9) + 8
Solution:
Solutions to these problems are given below:
(6.7) x 7.9
=52.93 In this solution, all 4 digits are significant figures.
(49.84) + 8
= 57.84 In this solution, all 4 digits are significant figures.



