Hi friends, I hope you all are well. In this post, we will talk about scientific notation. Scientific notation is an essential tool that scientists and engineers can use. Archemdies presented the idea of scientific notation in the 3rd century BC. His work and scientific notation ideas are based on the novel of time, known as place value.
Scientific notation ideas have evolved over many centuries but are finally represented by Archimedes. In the 16th or 17th century, mathematicians continued to adopt changes in them and invent many other new notable contributions like Rene Descartes who developed algebraic notation. Scientific notation is a way in which we can express large number values in short form in the form of an exponent or a decimal form.
Scientific notation not only simplifies the equation, but it can also help scientists and engineers to do calculations easily. In the United Kingdom scientific notation is also known as standard form or standard index form. Scientific notation is commonly used by scientists and on scientific calculators it is referred to as “SCI” display mode.

What is scientific notation?
Scientific notation in detail is given below:
Definition:
Scientific notation is defined as:
"it is the simplest way to express the large number into the small number or into in decimal form."
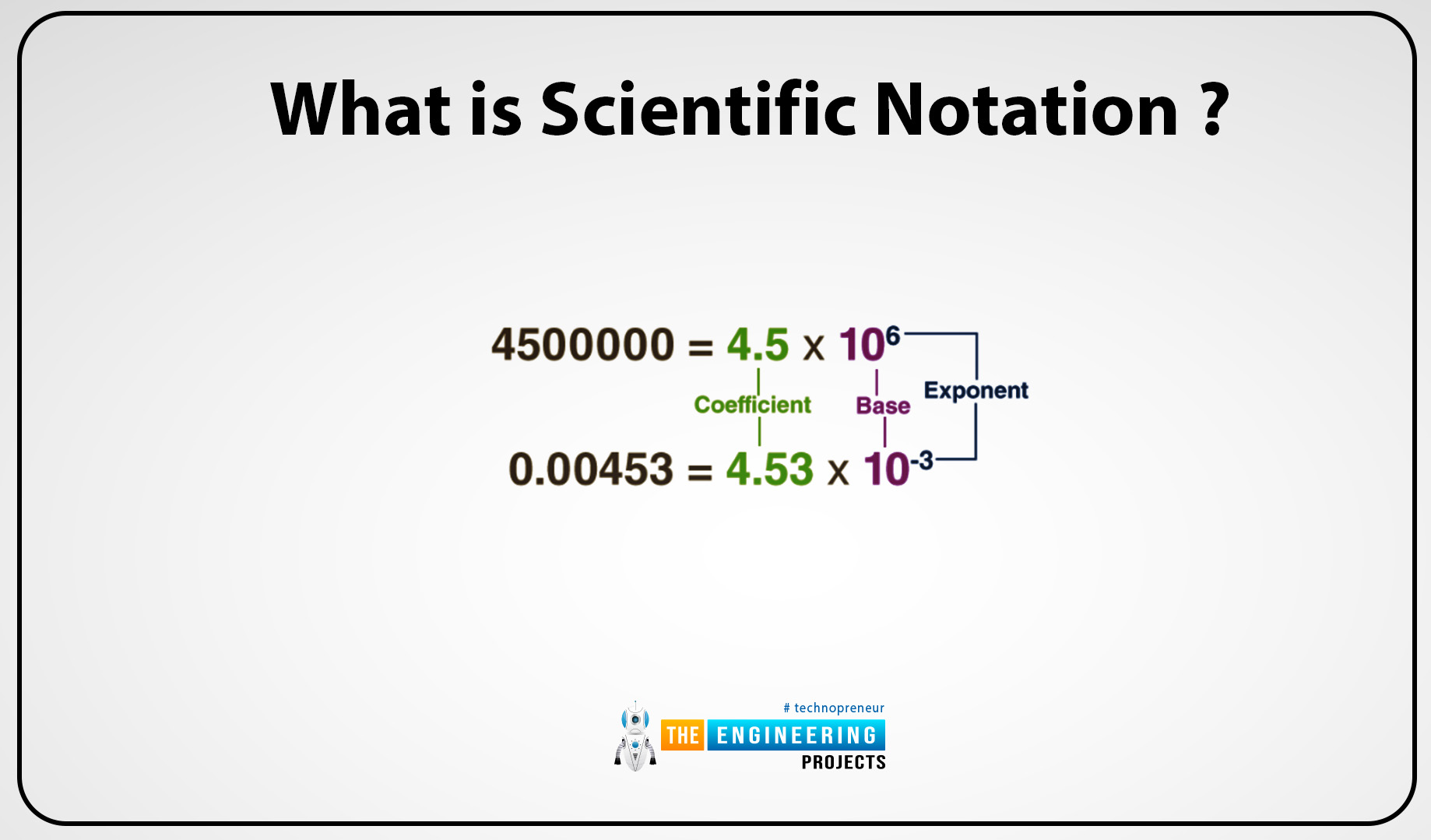
It can used by scientists, mathematicians, and or engineers to simplify the calculation and express the calculation in a very efficient way. In scientific notation, the number is expressed in the product form and they have two factors.
- A coefficient
- A power of ten
Generally, the scientific notation is written in:
N=m 10n
There:
- N is the number
- The coefficient is m. It is equal to 1 or less than 10.
- The integer exponent is n.

Example:
Some examples of scientific notation are given below:
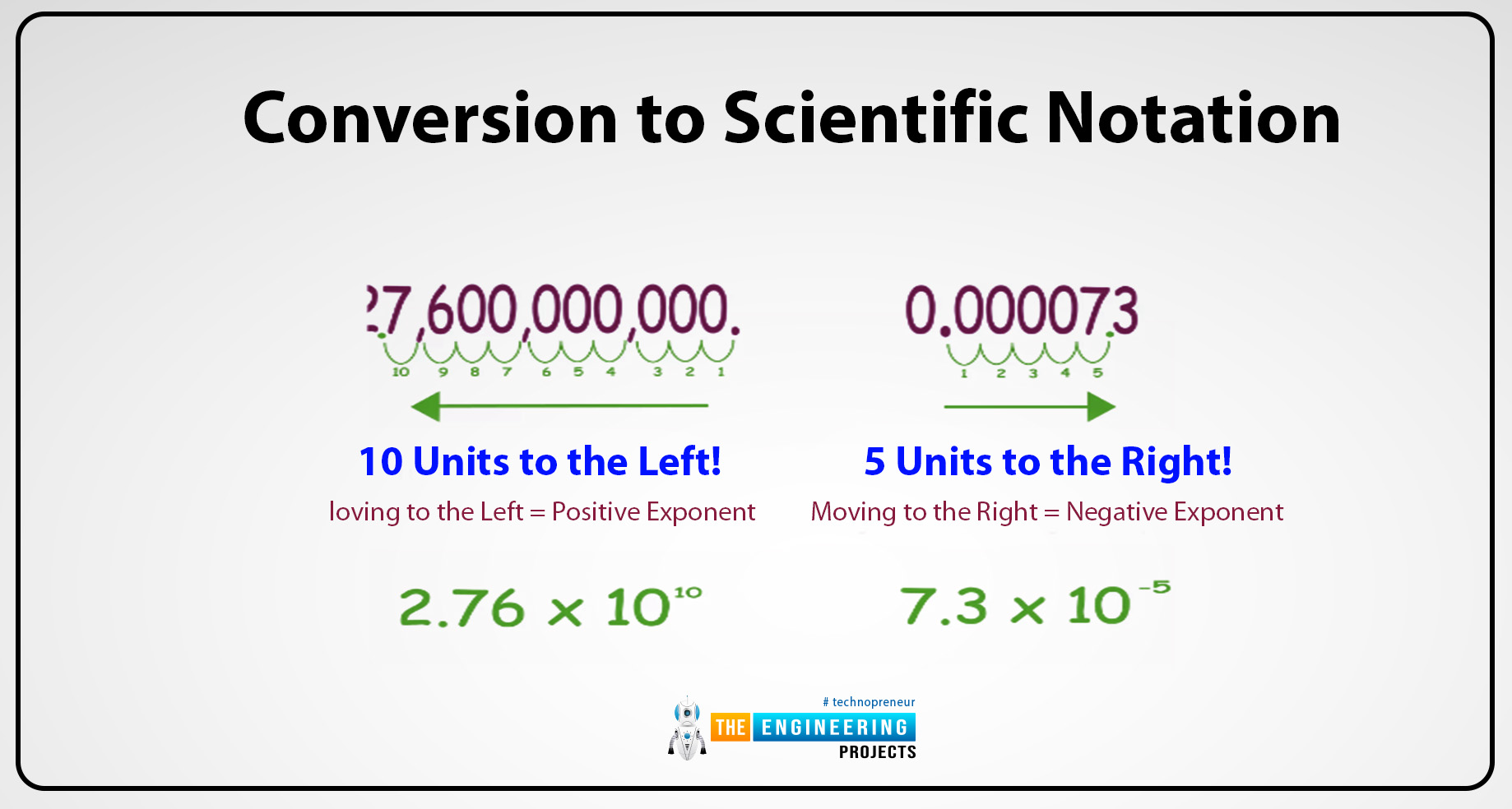
Covert 89,700 to scientific notation.
Firstly move the decimal to get 8.79
The decimal moved 3 places to the left, then the exponent is 8.
Then the scientific notation is 8.79103
Convert 0.0000023 into scientific notation:
Firstly move the decimal to get 2.3.
The decimal moved 6 places, then the exponent is 2.
Then the scientific notation is 2.3106.
Normalized notation:
We can write any real number equation in the form of m10n in various ways. In the normalized scientific notation, the value of m is 1 or greater than 1 but it is always less than 10 and the value of n depends upon the larger value or decimal place. thus equation 550 can be written as 5.50102. this scientific notation helps to compare the number easily in an efficient way if the exponent value is large that means that the number is normalized as compared to smaller exponents. The order of magnitude can be assumed when we subtract the exponent by separating the numbers.in the table of logarithms, we can use this form of numbers to solve the log questions. The exponent in the normalized equation is negative if the value ranges between 0 and 1 for example: 00.6 then it can be written in 610-2. the exponents may be equal to 10 if the real number value is large like 0.0000000009 then it can be written as 910-10.
In many fields, typically or generally normalized equation is used to express large numbers of values into simple and efficient decimal form. Exponential notation is also referred to as normalized notation. But in different fields, unnormalized or simple notation or equations can be used. Generally, the latter term of notation is more used where the value of m is not suppressed in the range between 1 to 10 and the base of the exponent may be changed or other than the 10.

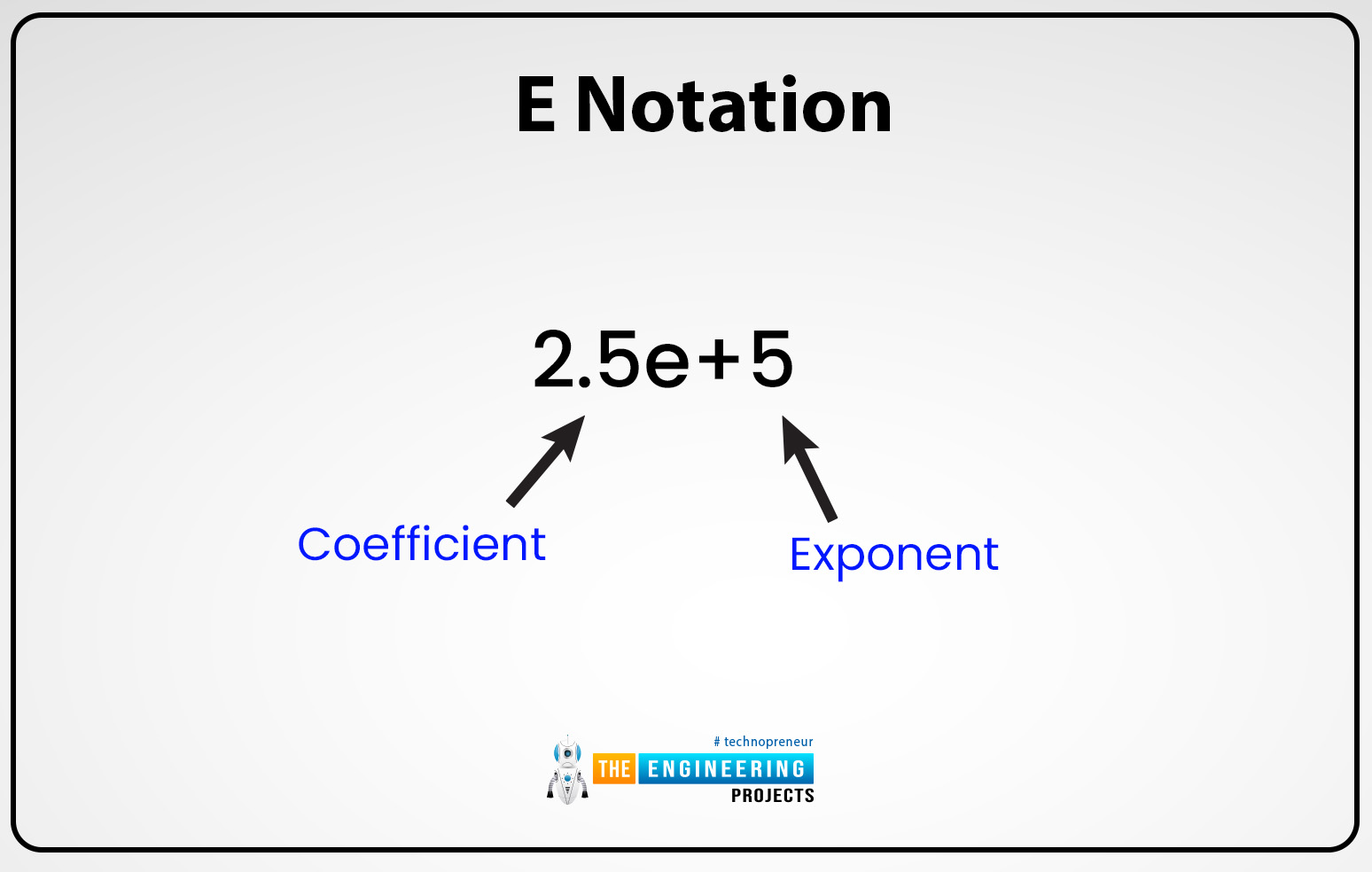
E notation:
Generally, calculators or computer programs use small or large number values to present scientific notation or in some calculators, all the numbers are present or configured uniformly.
The capital letter “E” or the small letter “e: can be used to represent or express the exponent which means “ten raised to the power of”. Typically in all computers or programs scientific notation or normalized notation can be abberived or represented in different styles. But the equation men is the scientific notation like m is the coefficient and the e is base 10 or n is for the exponent and it can be written as men or m10n. For example, 1.000 can be written as 1103 or also written as 1e3.
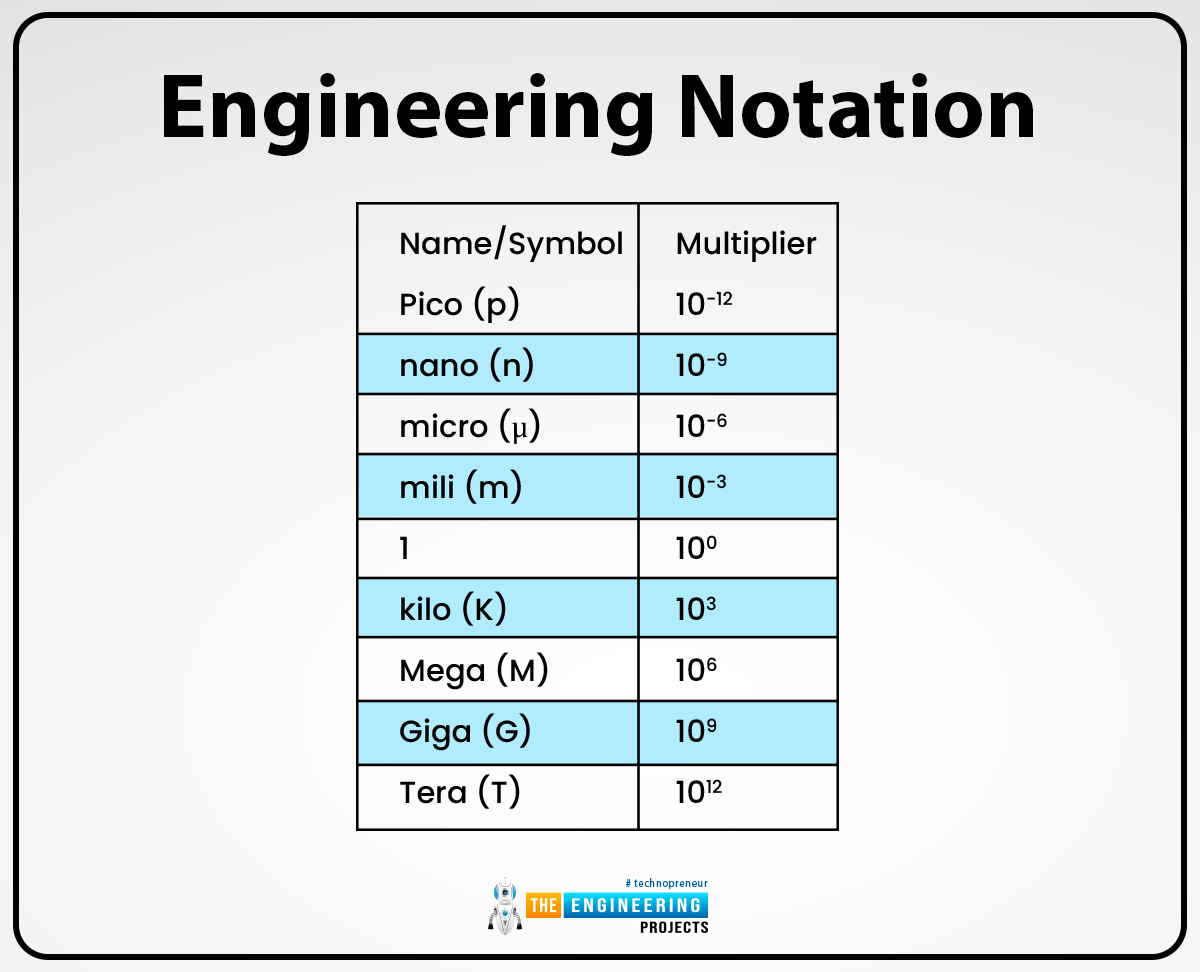
Engineering notation:
On the scientific calculator, the engineering notation can be written or expressed as “ENG”. The engineering notation is different from normalized notation because the value of exponent n is suppressed in normalized notation. Thus the value of m ranges in 1 ≤ |m| < 1000, other than 1 ≤ |m| < 10. So that's why sometimes the engineering notation is also known as scientific notation.
In engineering notation, the exponent value can be orally read by using prefixes such as nano, pico, Giga, and others. For example, 14.510-9 can as read as fourteen-point-five nanometers and can also be written as 14.5nm.
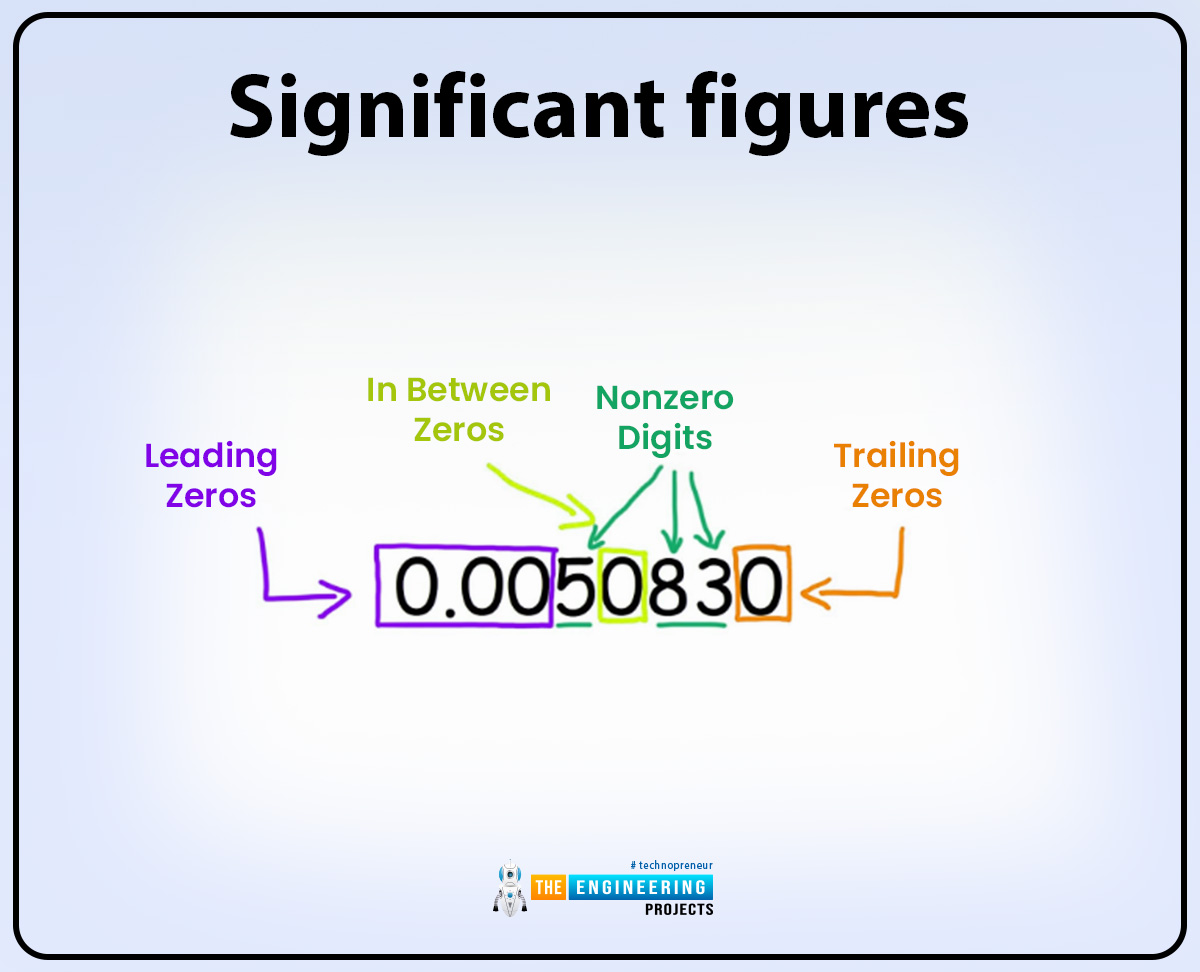
Significant figures:
The number of digits in the value is used to find the degree of accuracy and precision in a value.
Significant figures include all nonzeros or zero digits but the first and the last zero digits are not significant figures if zero is present in between the numbers like 1,2,3,4,5 and so on then it is also called a significant figure. Some examples are given below:
456709800 In this value 7 significant figures are present and at the last two zero is only a placeholder and not referred to as significant figures.
Then 008809 in these values there are 4 significant figures present and the starting first two zeros are not called significant figures.
So when we convert 123459900 values into normalized or scientific notation then all significant figures are present and the nonsignificant figure is removed as 123459900 has 7 significant figures then it can be written in scientific notation as 1.234599108 or also written as 1.23459900108. thus the advantage of scientific notation is to signify the significant figures efficiently.
Estimated final digit:
In scientific measurement, it is essential to record or measure all known digits from the measurement which can be calculated, and then estimate one or more digits if any information about this digit is acquirable. The estimated digits provided more information and became a significant figure because the estimated digits can provide more accurate and precise information about the leading and the ending digits.
The information that we can take from the estimated digit can help in the notation. This information also helps to choose the final digits or digits that are present in the value. For example, the estimated mass of a proton can be equal to 1.67262192369(51)10-27 kg. But in this value, the error occurs when we estimate the digit inefficiently and can be written as 5.110-37 and this estimated digit can increase the standard error or some other possible errors.
Rules for scientific notation:
The rules that are used to convert the number into scientific notation are given below:
Identify the coefficient
Determine the exponent
Base
Non-zero integer
Positive or negative integer
Add or subtract the coefficient
Arithmetic operation with scientific notation
Identify the coefficient:
When we move the decimal point in the value then the original number which becomes the coefficient a is taken like 230000 then the decimal moves in it and becomes 2.3 and the 2 becomes the coefficient in the scientific notation.
Determine the exponent:
Count the number of decimals that we moved in the value and this count becomes the exponent. For example: We have a value of 46000
Then it becomes, 4.6
The total no of decimals that we moved in the value is 4 then the exponent is 4 the value becomes 4.6x104.
Base:
The base of the exponent in the scientific notation is always 10.
Non-zero integer:
The exponent is always a value it is always a non-zero integer like 104 or 108.
Positive or negative integer:
When we move the decimal from right to left then the exponent integer is positive. Example:
46000 then 4.610+4
When we move from left to right then the exponent integer is negative. Example
0.00677 then 6.7710-3
Add or subtract the coefficient:
If the exponent is the same then we simply add or subtract them. Because the same exponent can be added or subtracted and also we can multiply or divide with them. For example:
3.4106 + 9.7106
The exponent is the same then we add them and then rewrite
3.4+9.7=10.04
Then rewrite them into scientific notation
10.04106 then the new scientific notation is
1.004107
Arithmetic operation with notation:
Division:
In the division method, we divide the coefficient and subtract the exponent. An example is given below:
81062104= 8106-42
=4102
Addition and subtraction:
To add or subtract the scientific notation, the same exponent must be necessary. And adjust the equation if needed. An example is given below:
= 2.6103+ 4.0104
Then firstly we adjust the equation to same the exponent of both equations,
2.6103= 0.26104
Then add or subtract them,
=0.26104+ 4.0104
=4.26104
Multiplication:
When we multiply the scientific notation then we add the exponent and multiply the coefficient.
Such as,
=(2104) (6102)
Then,
= (26) 104+2
So,
= 12108
Application of scientific notation in the real world:
Real-world applications of scientific notation in different fields are given below:
Chemistry:
Chemists use scientific notation to measure or calculate the atomic size or the atomic level. Such as Avagardo’s number which can be written scientific notation 6.0221023 which can be approximately equal to the one mole in an atom or a molecule.
Astronomy:
In space, astronomers used scientific notation to calculate the vast distance. Because in space the distance between the moon, the sun, and other planets is vast so that's why to calculate this distance in a short or efficient way astronomers used scientific notation. For example, the distance between the Earth and the nearest star is approximately equal to 4.241013 kilometers.
Engineers:
Engineers work on a large scale and calculate the calculation in a very precise and efficient way so that is why they use scientific notation to express large number calculations in short form. For example, the circumference of the earth which can calculated by engineers is 4.007107.
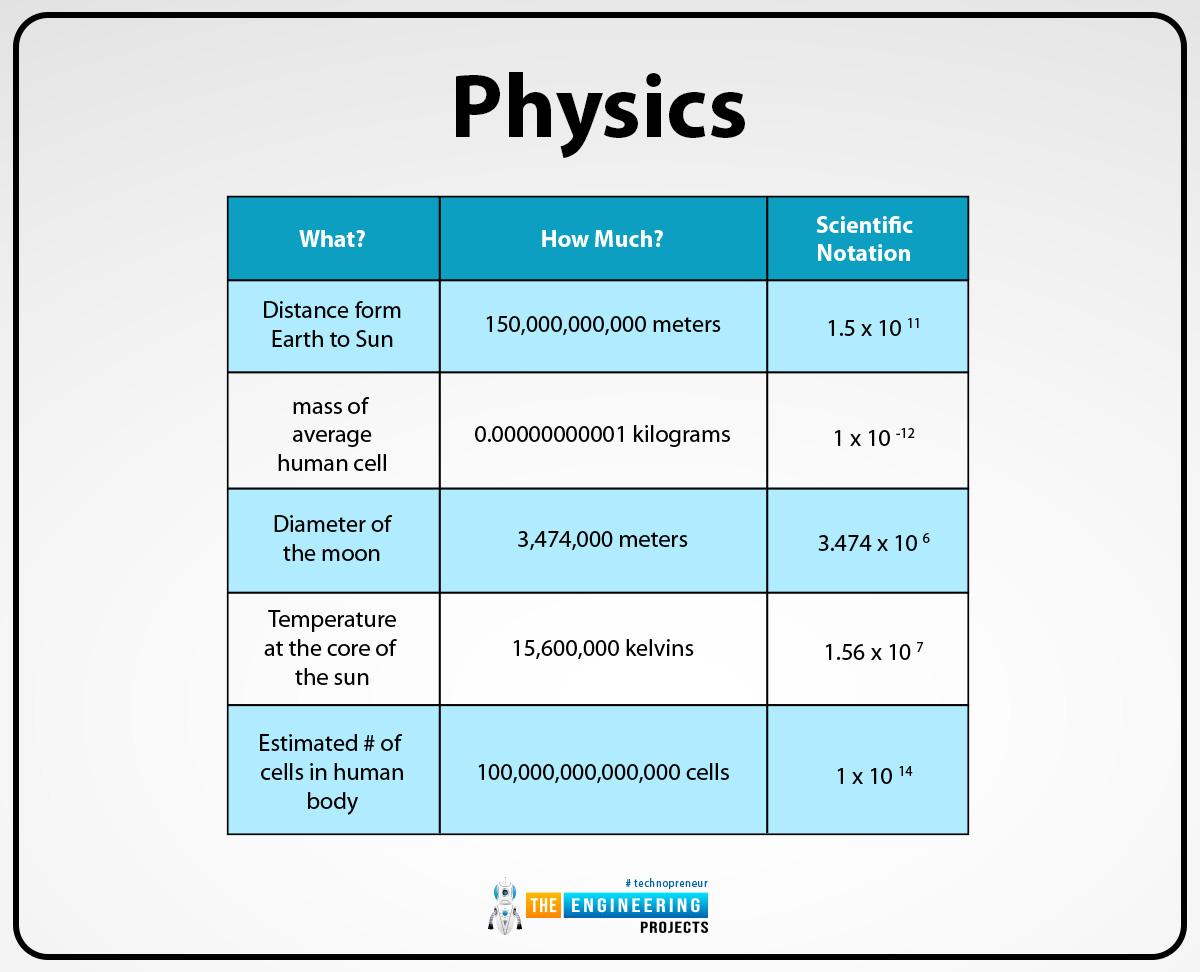
Physics:
In physics, scientists can deal with very large and small quantities of measurements so that’s why to write these measurements in an efficient way they can use the scientific notation method. For example, the speed of light is 3.00108.
In education the role of scientific notation:
To become a scientist or for a scientific education understanding the scientific notation is essential. Scientific notation education starts in middle school but is explained in detail at higher levels. To become a scientist and, if we choose the engineering and technology career then the education of scientific notation is compulsory. because it helps them to calculate or, measure the very large or small measurements in a very precise or accurate form.
Challenges and misconceptions:
With the advantages and utility of scientific notation, it also becomes difficult or challenging for beginners. The common misconceptions that can be faced by beginners are given below:
Arithmetic operations rules can't be understood or can't be used precisely.
Zero can be confused with exponent.
The decimal point can't be placed properly.
Rules which are used for scientific notation can be misunderstood.
Strategies that can be used to manage or overcome these misconceptions or challenges include:
Understand the rules of scientific notation step by step and follow instructions.
Try to solve numerous examples without help.
Understand the rules and solve the arithmetic operations.
Future perspectives:
With the development of modern science and technology, the use of scientific notation is also increased and it can also be improved from time to time. In modern science and technology, very large and small measurements can be calculated so that’s why the scientific notation method is used to express calculation effectively and accurately because scientific notation also helps to overcome or analyze errors in calculations.
Examples:
Examples of scientific notation are given below:
The mass of the electron is approximately equal to 0.000000000000000000000000000000910938356 kg
But we can write in scientific notation as,
= 9.10938356×10−31
The circumference of the earth is approximately equal to 40000000m
Then we can write in scientific notation as
= 4107
The distance between the sun and earth is approximately equal to 149,600,000 kilometers
In scientific notation, it can written as:
=1.496108
The mass of hydrogen is approximately equal to 0.00000000000000000000000167kg
In scientific notation, it can be written as,
=1.6710-27
The value 564300 can be converted into scientific notation and written as
=5.643105
Problems:
Some problems are given below:
Conversion:
Convert the following problems into scientific notation:
456800
0.005544
98076
5544320
0.00000000009
9888800000
Solutions:
Solutions to these problems are given below:
4.568105
5.54410-3
9.8076104
5.544320106
910-11
9.8888109
Multiplication:
Multiplication problems are given below:
(2108 ) (4104)
(2.0104) (2102)
Solution:
Solutions to these problems are given below:
(24) 108+4
=81012
(2.02) 104+2
=4.0106
Division:
Division problems are given below:
5.61097.0103
8.41052.0102
Solution:
A solution to these problems is given below:
8.0105
4.2103
Addition and subtraction:
Perform the following operations with numbers in scientific notation:
(5.0104)+(2.5104)
(6103) + (4.0103)
Solution:
A solution to these problems is given below:
7.5104
6103



