
Hi friends, I hope you are all well. Today we can talk about the dimensions of all physical quantities which include the base quantities and the derived quantities. Dimensions of physical quantities are the fundamental part that helps us understand the physical and natural properties of any physical quantity. In modern science and technology, in engineering, and in different fields of physics where physical quantities units are used, the dimensions of these units help to derive a new formula and are also used in derivations. Dimensions of physical quantities also convey the detail of the types of physical quantity.
Dimension of physical quantities also helps to check the correctness of the equation and the formula that we can derive or use to solve the problems. Dimension of the physical quantities systematically expressed the physical quantities units. For analysis of the formula and the physical quantities, we can also use the dimensions of these quantities. Now we can start our detailed discussion about the dimensions of physical quantities which include the base quantities dimensions, derived quantities dimensions, and the application and analysis of the physical quantities in physics.

What are physical quantities?
Definition:
Physical quantities are defined as:
“The quantities which can be measured and quantified by measurements are termed as physical quantities.” For example mass, length weight, electric current, and many other various quantities. These physical quantities can be expressed in the algebraic form and when measured we can use different units for their measurements. To know the correctness of these units we can use dimension analysis.
For example for the quantity length we can use the unit meter and their symbol is m so by using the dimension of the meter we can verify them.
Types:
There are two main types of physical quantities units which are given below:
Base quantities
Derived quantities
The units that can be used to describe these physical quantities are known as base quantity units and the derived quantity units.

Dimensions of physical quantities:
Dimension of physical quantities is defined as:
"The fundamental quantities which can be expressed in the form of raised power to describe the physical quantities are termed as dimensions of physical quantities."
The unit and the dimension of the physical quantity are written in the square brackets. For example, the unit of length is m and the symbol is m but their dimension is L.
The dimensions of base physical quantities and the derived physical quantities in detail are given below:
Base physical dimensions and their units:
There are seven basic base physical quantities units which are also known as the building blocks units from which other units are derived. The dimensions of these base physical quantities with their units and definitions in detail are given there:
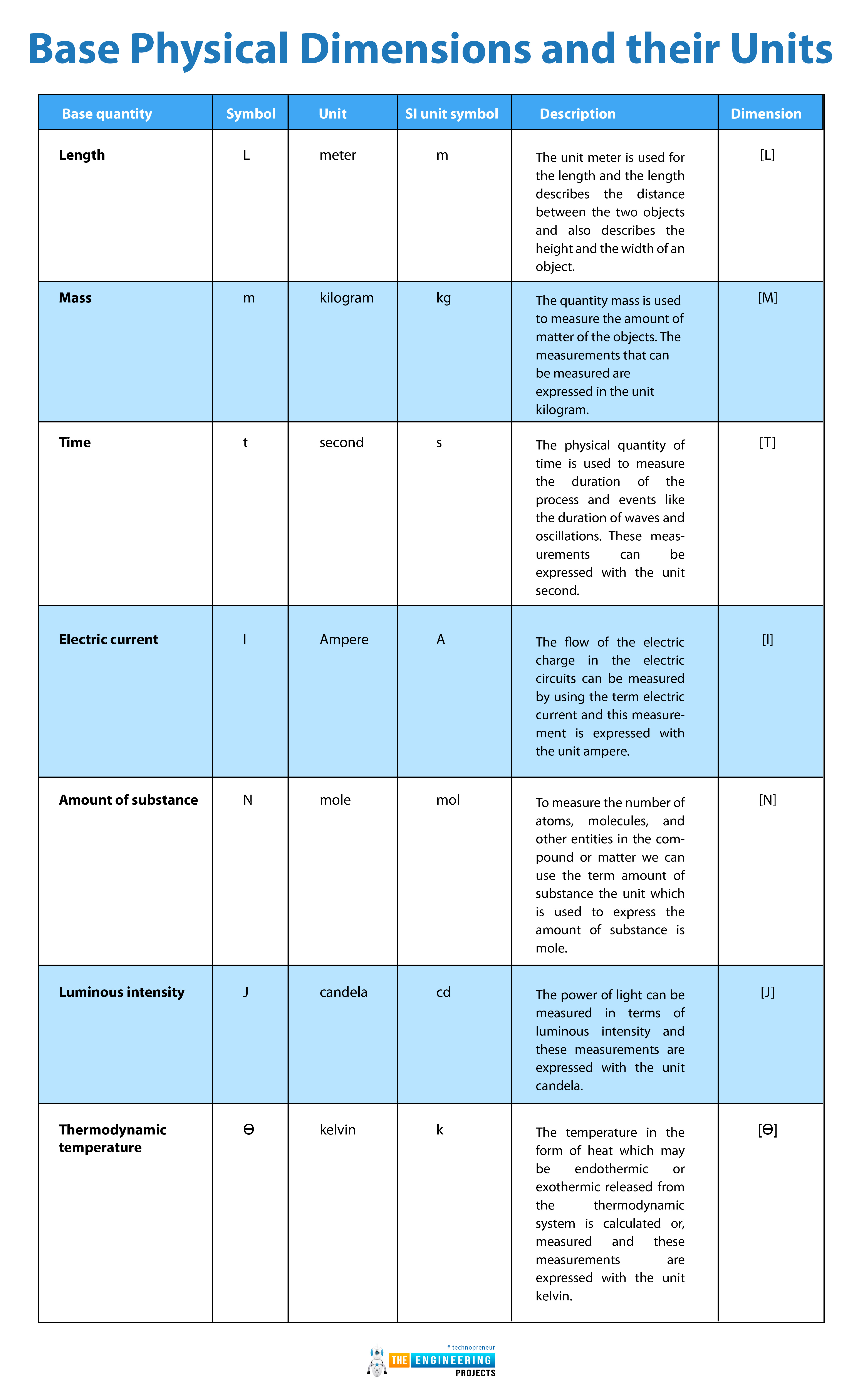
Base quantity |
Symbol |
Unit |
SI unit symbol |
Description |
Dimension |
Length |
L |
meter |
m |
The unit meter is used for the length and the length describes the distance between the two objects and also describes the height and the width of an object. |
L |
Mass |
m |
kilogram |
kg |
The quantity mass is used to measure the amount of matter of the objects. The measurements that can be measured are expressed in the unit kilogram. |
M |
Time |
t |
second |
s |
The physical quantity of time is used to measure the duration of the process and events like the duration of waves and oscillations. These measurements can be expressed with the unit second. |
T |
Electric current |
I |
Ampere |
A |
The flow of the electric charge in the electric circuits can be measured by using the term electric current and this measurement is expressed with the unit ampere. |
I |
Amount of substance |
N |
mole |
mol |
To measure the number of atoms, molecules, and other entities in the compound or matter we can use the term amount of substance the unit which is used to express the amount of substance is mole. |
N |
Luminous intensity |
J |
candela |
cd |
The power of light can be measured in terms of luminous intensity and these measurements are expressed with the unit candela. |
J |
Thermodynamic temperature |
Ө |
kelvin |
k |
The temperature in the form of heat which may be endothermic or exothermic released from the thermodynamic system is calculated or, measured and these measurements are expressed with the unit kelvin. |
Ө |
Derived physical units with their dimensions:
Derived units are derived from the seven basic base quantities units such as area, volume, power, and many others. Some of these derived units with their symbols and dimensions are given below:
Derived Quantities |
Symbols |
Formula and relation with other quantities |
Dimensions |
Dimensions related to the formula |
SI units |
SI units symbol |
Force |
F |
mass acceleration |
m= M acceleration = LT-2 |
MLT-2 |
Newton |
N |
Area |
A |
length breadth |
L= L breadth=L |
M0L2T0 |
Meter square |
m2 |
Density |
ρ |
mass volume |
m= M volume = L3 |
ML-3T0 |
Kilogram cubic per meter |
kgm-3 |
stress |
σ |
Forcearea |
F= MLT-2 A= L2 |
ML-1T-2 |
Newton per meter square |
Nm-2 |
Surface energy |
σs |
energyarea |
energy= ML2T-2 Area = L2 |
ML0T-2 |
Candela meter per second square |
Jm-2 |
Impulse |
J, imp |
force time |
force= MLT-2 Time= T |
MLT-1 |
Newton per second |
Ns-1 |
Strain |
ε |
change in dimensionorginal dimension |
Dimensionless |
—- |
—--- |
—--- |
Hubble constant |
H0 |
velocity of recession distance |
velocity= LT-1 distance= L |
M0L0T-1 |
Per second |
s-1 |
Coefficient of elasticity |
δ |
strssstrain |
stress= ML-1T-2 strain=1 |
ML-1T-2 |
Newton per meter square |
Nm-2 |
Volume |
V |
Length height breadth |
length= L height= L breadth= L |
M0L3T0 |
Cubic meter |
m3 |
Thrust |
N |
Force |
force = MLT-2 |
MLT-2 |
Newton per meter square or Pascal |
Nm-2or Pa |
Linear acceleration |
a |
velocitytime |
velocity= LT-1 time= T |
M0LT-2 |
Meter per second square |
ms-2 |
Work |
W |
Force distance |
force= MLT-2 distance= L |
ML2T-2 |
joule |
J |
Specific volume |
v |
volume/mass |
volume= L3 mass= M |
M-1L3T0 |
Cubic meter per kilogram |
m3kg-1 |
Specific gravity |
s.g |
density of material density of water |
—--- |
Dimenonless |
||
Tension |
T |
Force |
force= MLT-2 |
MLT-2 |
Newton meter per square and Pascal |
Nm-2 or Pa |
Surface tension |
Y |
force/ length |
Force= ML0T-2 length = L |
ML0T-2 |
Newton per meter |
Nm-1 |
Radius of gyration |
k |
distance |
distance= L |
L |
meter |
m |
Angular velocity |
ω |
angle/ time |
angle= L time= T |
LT-1 |
Radian per second |
rs-1 |
Momentum |
p |
Mass velocity |
mass= M velocity= LT-1 |
MLT-1 |
Kilogram meter per second |
Kg ms-1 |
Rate flow |
Q |
volume/ time |
Volume =L3 Time= T |
M0L3 T-1 |
Cubic meter per second |
m3s-1 |
Frequency |
λ |
No vibrations/ time |
Time= T |
M0L0T-1 |
meter |
m |
Heat |
Q |
energy |
energy= M1L2T-2 |
M1L2T-2 |
joule |
J |
Buoyant force |
force |
force= M1L1T-2 |
M1L1T-2 |
Newton |
N |
|
Plancks constant |
h |
energy/ frequency |
energy= M1L2 frequency= T |
M1 L2T-1 |
Joule second |
Js |
Dimensional analysis:
To derive the formula and the relationship between the different numerous physical quantities we can use a method or a technique known as dimensional analysis. Dimensional analysis can also be used to identify and determine the correctness of the equation and the formula and also change the units from one system to another systems. Dimensional analysis is based on the following points which are given there:
Principles of dimensional analysis
Steps involved in the dimensional analysis
Details of these points are given below:
Principles of dimensional analysis:
Principles of dimensional analysis include:
Derivation of formulas
Dimensional homogeneity
Conversion of units
Conversions of units:
We can convert the units with the help of dimensional analysis in some other units. But the units that can we convert are expressed in terms of the base units. Some examples of conversion of the units are given there:
The unit square per meter which we we used to express the velocity is converted into some other base unit like km/h through dimension analysis.
If we can measure the distance in the units meters then we can convert it into the other base units like meters per hour.
Dimensional homogeneity:
The formula or the equation that we may derive and use for solving the problems has equal and the same similar dimensions on both sides which proves that the equation is correct. if the dimensions on both sides are not the same it proves that the equation is not correct. So dimension analysis also helps to identify or determine whether the equation or formula is correct or not. Some examples are given there:
For example, the formula or area is A = Length breadth. The dimension of the area is L2 and on the other side, the dimension of length is L and breadth dimension is L so on both sides dimensions are the same proves that the formula is correct.
Another example is a force equal to F= ma and the dimension of force is MLT-2 and on the other side the dimension of m is M and the dimension of a is LT-2. so it proves that the formula is correct because the dimensions on both sides are the same.
Derivation of formulas:
We can derive the different authentic formulas by using numerous physical quantities with the help of dimensional analysis. Dimensional analysis helps to understand the property of quantity which we can use to derive the formula. Some examples are given there:
We can derive the period of the pendulum by using the dimension of time and distance.
We can also derive the formula for the force by using different physical quantities like mass, acceleration, and time and we can also check whether the equation is correct or not with the help of dimensional analysis.
Steps which are involved in the dimensional analysis:
The steps which are involved in the dimensional analysis are given there:
Set up the equation
Identify the base quantity
Write the dimensional formula
Solve for the unknowns
Set up the equation:
For dimensional analysis, it is essential to check or confirm that the equation or formula we are using has the same dimensions on both sides and they are equal to each other. Some examples are given below:
The formula which is used for work is W= force distance the dimension for work is the same and equal to the dimension of force and the distance.
Another example is the formula of force is F= ma and the dimension of force is equal to the dimension of mass and acceleration so that's why the dimension analysis helps to identify the equation is correct.
Identify the base quantities:
In dimensional analysis, it is essential to identify the physical quantities that we are using to derive the formula or to solve the problems. Some examples are given below:
Identify the mass, length, volume, and other physical quantities and then use their dimension for dimensional analysis.
Solve for the unknowns:
To identify the unknown physical quantities we can use the dimensions. And by the help of dimensions we can identify and determine the right physical quantity. Some examples are given below:
We can identify the gravitational constant G by using the dimensions and also determine their dimensions with the help of dimensional analysis.
For another example, we can determine the pendulum period by using the different dimensional equations, and after determining we can also identify their dimension with the help of dimensional analysis.
Write the dimensional formula:
In the formula that we derived or used to solve the problems, it is essential to write the dimension of all quantities that can be used in the formula. Some examples are given below:
The dimensional formula of the area is L2.
The dimensional formula of power is Ml2T-3.
Applications of dimensional analysis:
In the era of modern sciences and technology, engineers and other scientists measure complex quantities. Dimensional analysis helps to measure these complex quantities and also helps to derive new complex formulas and check the correctness of the derived formula by using the dimensions. Now in the modern era of physics and engineering, dimensional analysis can be used in many different fields. Some applications of dimensional analysis are given below:
Biophysics
Relativity
Plancks constant
Engineering
Biophysics:
In biophysics, we can study and understand how the substance in the body or biological tissues can be moved or flow. Because diffusion mechanism can be used and we can measure and express them in some units so that's why we can use dimension analysis in it also
Some examples are given below:
The coefficient of diffusion can be described as the flow of material from one to another place and its dimensional formula is L2T-1.
Relativity:
To understand the relationship between mass and energy we can use the dimensional analysis method. Because they help to determine or identify the quantities that can be used in their dimensions. some examples are given there:
The formula which can be derived by Einstein is based on the relationship between the mass and the speed of light the formula is F=mc2 and the dimensions of m is M and the dimension of c2 is LT-1.
Quantum mechanics:
In quantum mechanics, we can understand the energy levels in the atoms and with the help of dimensional analysis, we can check the correctness of equations and detail understand the the energy levels in the atoms. Examples of dimensional analysis in quantum mechanics are given there:
For dimensional analysis and understanding the energy level we can use the formula of Plancks constant which is E=hv in this h is for energy level v is for frequency and their dimension is ML2T-1.
Engineering:
In engineering dimensional analysis is used for stress and strain because they can design the new materials and check their capacity to bear the load. So that's why dimensional analysis is used to determine the dimensions of stress and strain. Their example is given there:
In engineering, the stress on the object at force per unit area and strain changes the length and their dimensional analysis ML-1T-2.
Conclusion:
Dimensional analysis plays a vital role in the modern era of science and modern technology because in this era we can measure complex physical quantities and checking the correctness of dimensional analysis is essential. It can also help to derive the new formula and understand the natural properties of the quantities. By using dimensional analysis scientists and engineers can achieve highly precise and accurate measurements of complex physical quantities.
With time when the physical quantities become more complex and developed then the dimensional analysis techniques can also be developed and adopt different changes in them. The steps that can included in the dimensional analysis can be developed and more steps are included for the analysis of complex physical quantities which helps the scientist to understand the quantities and give the most precise and accurate result according to complexity.



