Hi readers, I hope you are all well. In this post, we can talk about the vectors briefly. Physical quantities can be defined through magnitudes but some physical quantities can be defined through both magnitudes and direction, these types of quantities defined through both magnitude and directional properties are known as vectors, and the quantities that can be explained through magnitude, not with direction are known as scalars. some vectors are force, velocity, displacement, and acceleration.
Vectors can explain the direction and magnitude of the quantity but they can't provide their position. It is an essential tool of mathematics that can be used in physics for knowing the direction or magnitude. It cant be used in the 18th century but can be used in the modern era of the 19th century late and it can be presented by the scientists Oliver Heavisde and Willard Gibbs they can develop the vector analysis which can be used to express the modern laws of electromagnetism which can be presented by the James clerk maxwell.
In different fields of physics like mechanics, and mathematics or in engineering, vectors can be used to explain the different qnatites in mathematical form with magnitude and direction. Now we can start are brief discussion about vectors their definition, mathematical representation, operations, types, and their application in different fields of physics.

Vectors:
Definition, mathematical representation, operations, and their application in different fields of physics in detail are given below:
Definition:
It can be defined as:
"The quantity which can described through both direction and magnitude is known as vector quantity or vectors."
In mechanics or geometry firstly term vector can be used but in some articles, the word or term vector can also be used for tuples. because mostly in mechanics which is the branches of physics vector quantities are used for magnitude and direction. some examples of vector quantities are given there:
- Magnetic field: In the magnetic field the moving charges represent the force that they can experience.
- Acceleration: The rate of change of velocity can be represented by a vector.
- Displacement: The position which can be changed by a moving object can be represented through a vector.
- Momentum: The product of velocity and mass can represented through a vector.
- Velocity: The direction and speed through which an object can be moved are represented through a vector.
- Electric field: In the electric field the unit positive charge represents the force which they can be experienced.
- Force: the object that can be pulled or pushed then their direction and magnitude can be represented by a vector.
Representation of vectors:
Representation of vectors in detail is given there:
Bold letter:
The vector quantity can be represented through the bold letter. For instance, the normal letter is v but for the vector, it can be written in bold form like v. Another example is the normal letter is written as a,b, and c but if it can be used for vector it can be written as a, b and c.

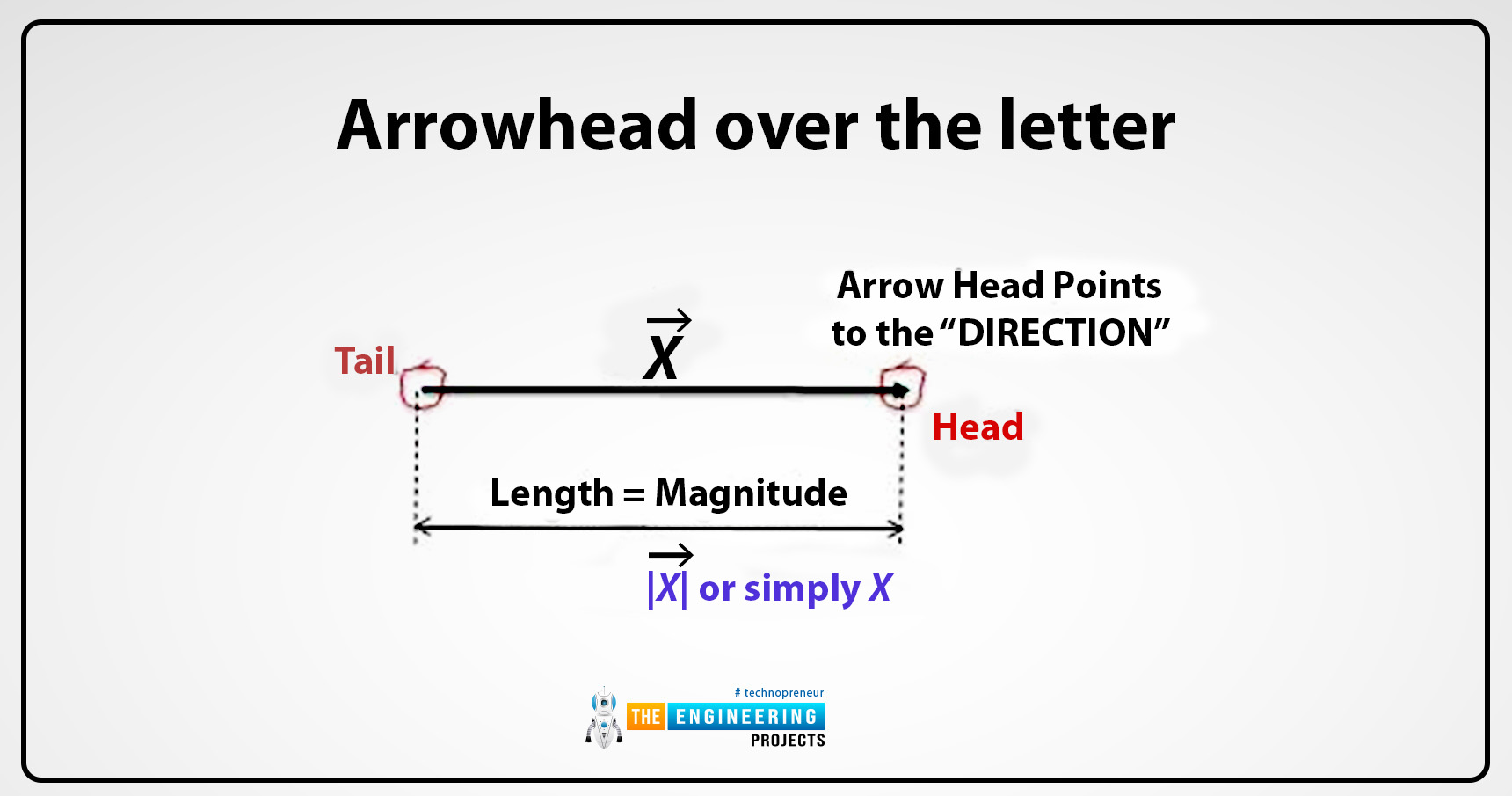
Arrowhead over the letter:
The vectors can also be represented by putting the arrowhead over the letter. Some examples are given there:
Graphical representation:
Vectors can also be represented in graphical form through an arrow. In the graphical representation, the arrow points to the direction of the vector, and the length of an arrow can represent the magnitude of the vectors.
For instance, a vector can cover the displacement from point A to point B then the arrow length represents the magnitude and the arrow point represents the direction from point A to point B.

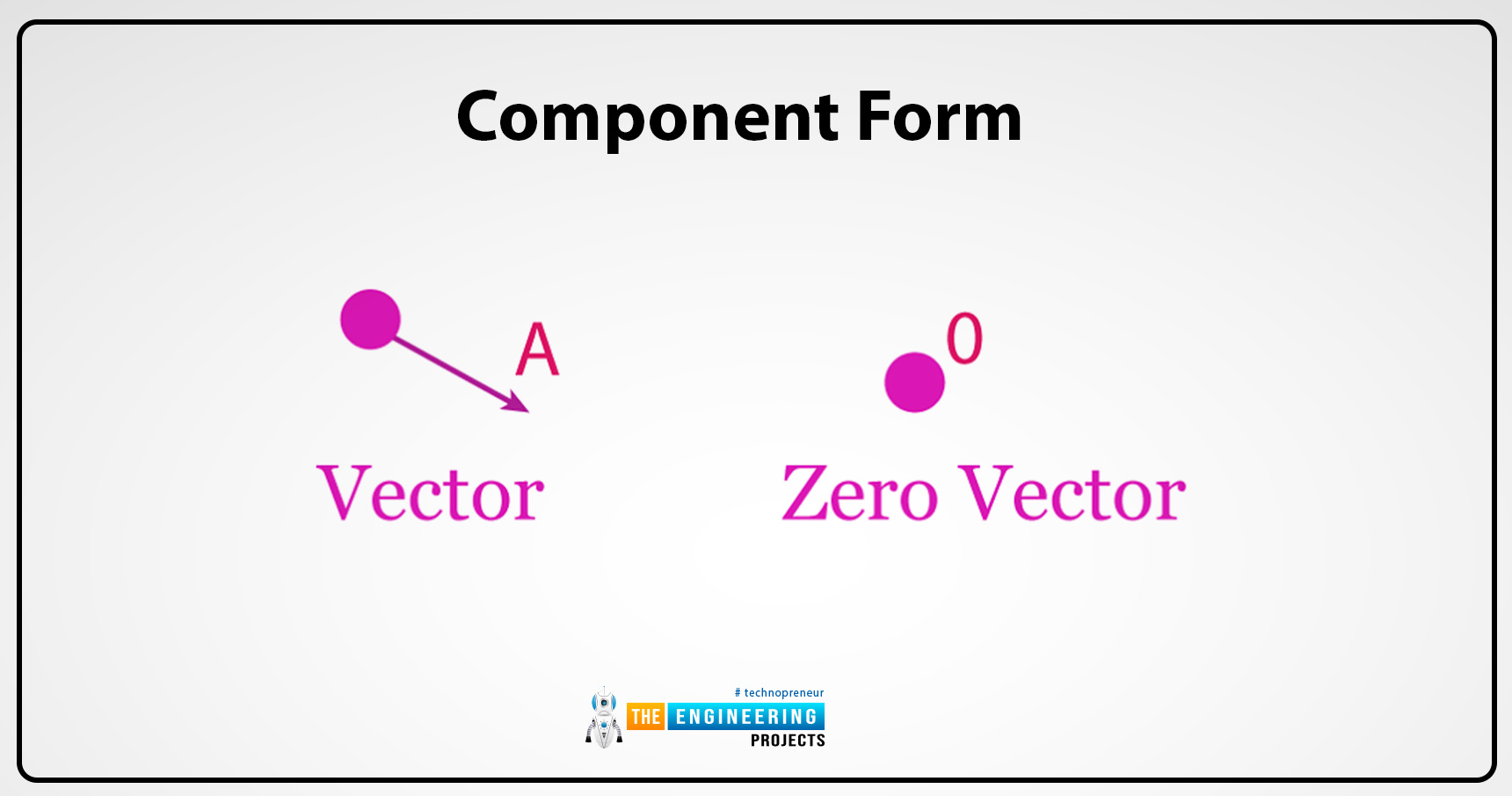
Component form:
The components of the vectors can also be expressed in the coordinate axis. Their components can be expressed in the two-dimensional cartesian coordinate system or the three-dimensional cartesian coordinate system. In a dimensional coordinate system, there are two axes x and y so the vector A in the two-dimensional system can be broken and written as AX on the x component and Ay in the y component.
But in the three-dimensional cartesian coordinate system x, y, and z are the three components and the vector A is written as Ax on the x component, Ayon the y component, and Az in the z component.

In the two-dimensional coordinate system, the vector A is mathematically written as;
A = AXi + Ayj
In the three-dimensional coordinate system, the vector A is mathematically written as;
A = Axi + Ayj + Azk
There i, j, and k are the unit vectors in the direction of vector components x, y, and z.
Types of vector:
Various types of vectors are used in physics or mechanics some types of vectors with their details are given there:
Null or zero vector
Equal vector
Position vector
Negative of a vector
Like or unlike vector
Unit vector
Displacement vector
Coplanar vector
Co initial vector
Collinear vector
Their description is given there:
Null or zero vector:
A null vector is also termed a zero vector. In vector is referred to as a zero or null vector when its magnitude is zero and there is no specific direction where the arrow points. In null or zero vector the length of magnitude is also zero. Their starting and ending points are the same. For instance, the vector OQ has the line segment and the starting point is O and the end is at the same point Q so their magnitude is 0.
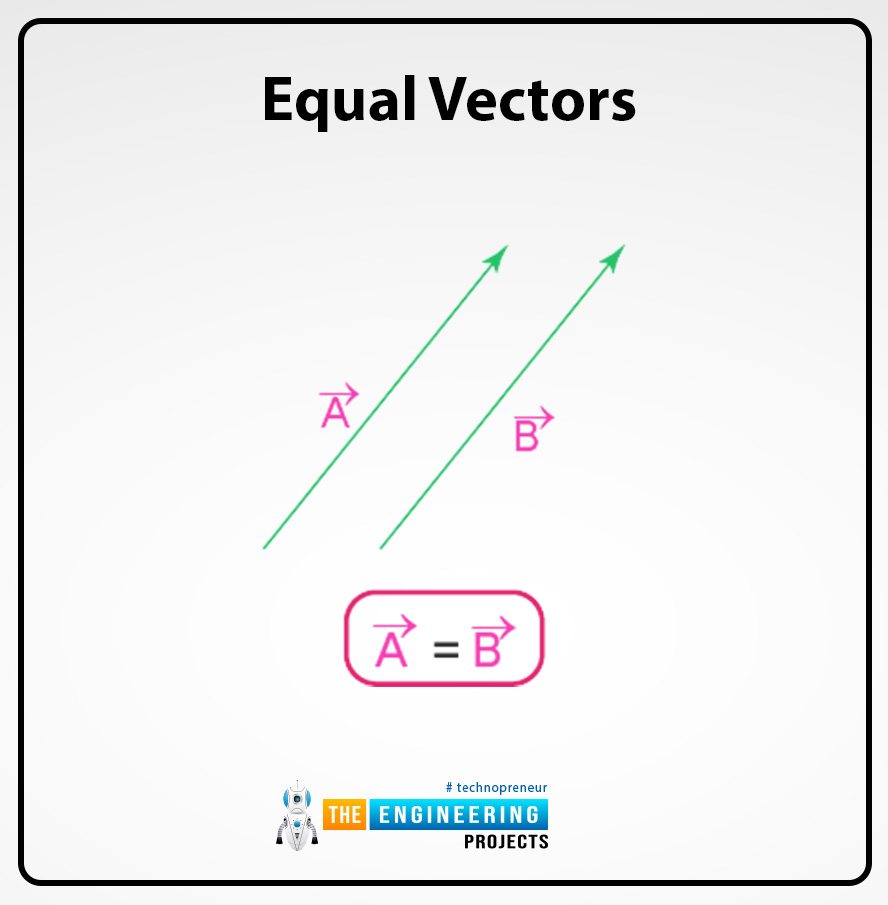
Equal vectors:
Two different vectors are termed equal vectors if they have equal magnitude and also their direction. Rather they may have different starting points but their magnitude and the direction are same. For instance, if the vector magnitude is equal to the magnitude of vector b and their arrow is pointed in the same direction.
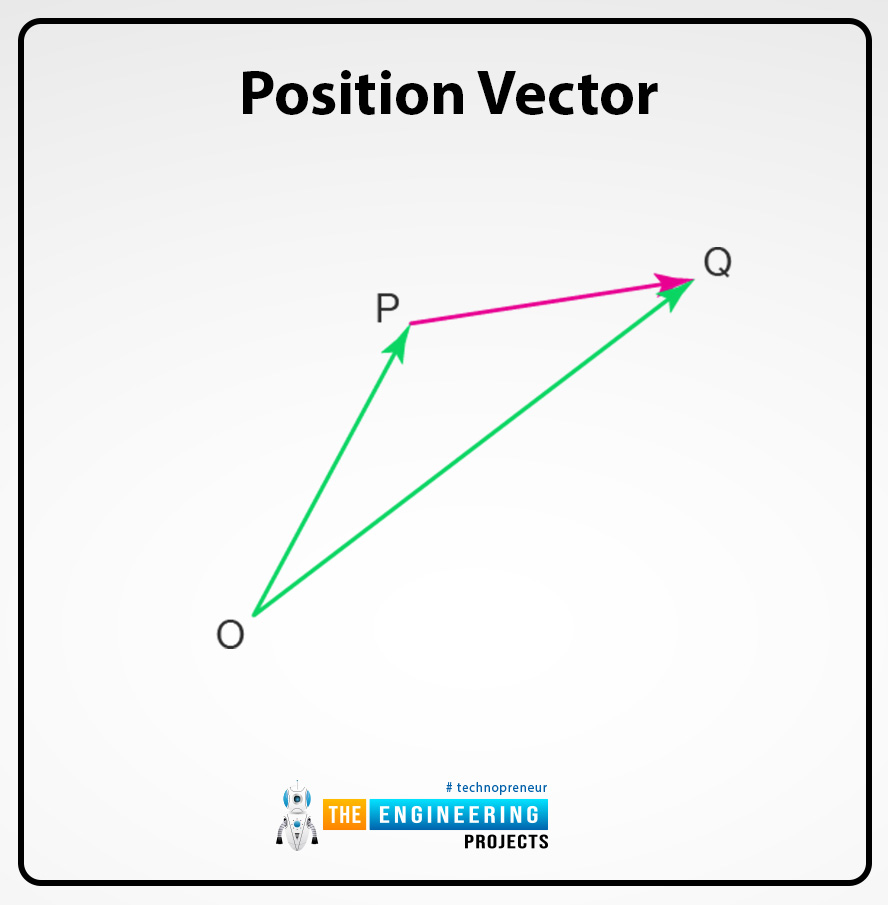
Position vector:
The vector can represent the origin and the position at any point related to the initial or origin point. Position vector can describe the direction of a vector from the main origin point to the endpoint.
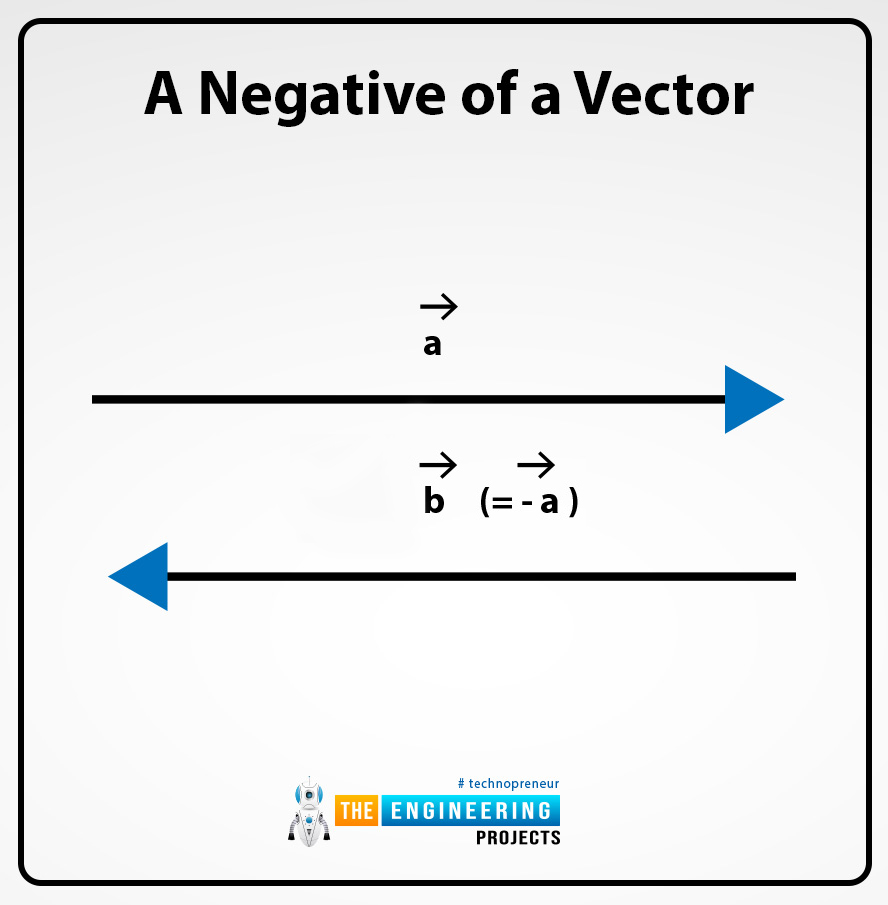
A Negative of a Vector:
The vector is termed as negative a vector if the vector which is given has the same magnitude and direction but at a point, any vector can change its direction means they have the same magnitude but have opposite directions so this vector which has the same magnitude but the opposite direction is known as negative of the vector. For example, vector A and vector B have the same magnitude but they have opposite directions and are written as A = -B
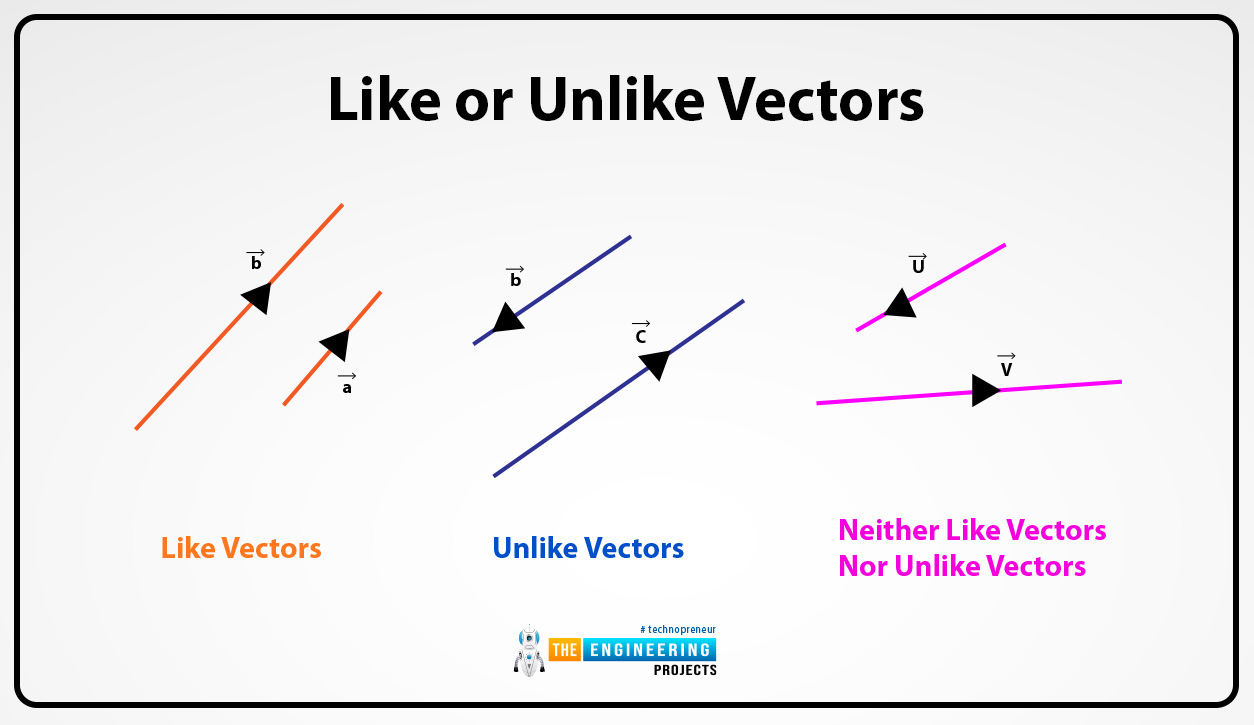
Like or unlike vectors:
The vectors are termed as like vectors if they have the same direction but if the vectors do have not the same direction then they are called unlike vectors. For example, if the vector AB has the same direction then they are like vectors but if vector AB does have not the same direction then they are unlike vectors.
Unit vector:
The vectors are termed unit vectors if they have only one magnitude. A unit vector is slo referred as the direction vector. The formulas that are used for unit vectors are:
V = VV
V represents a unit vector, V represents a vector, and V represents the magnitude of a vector.
Displacement vector:
If the quantity can be a displacement from point A to point B then the displacement between the AB is termed a displacement vector. For example, if a quantity is moved from point A and reaches point B then the distance between these points is termed a displacement vector it can also be termed the position vector.
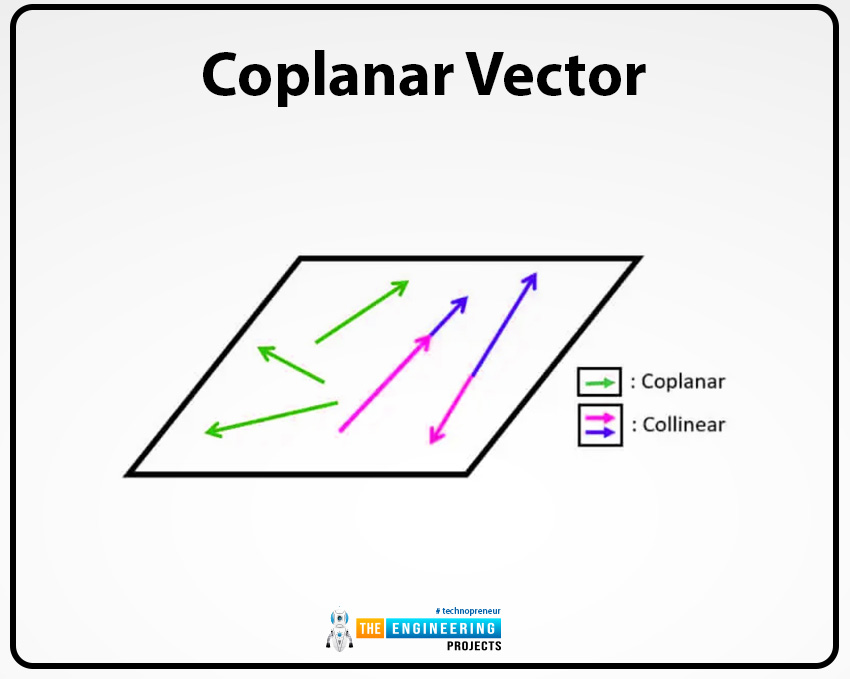
Coplanar vector:
The vectors that are placed in three-dimensional space with the same plane then it can be termed as the coplanar vectors. All vectors are parallel to each other in the same plane.
Collinear vector or parallel vector:
Two vectors are termed collinear if they are parallel to each other and not dependent upon the magnitude or direction. Collinear vectors are also termed parallel vectors. For example, if the vector A and vector B are opposite in direction and both have different magnitudes but they are parallel to each other then it can be called a collinear or parallel vector.
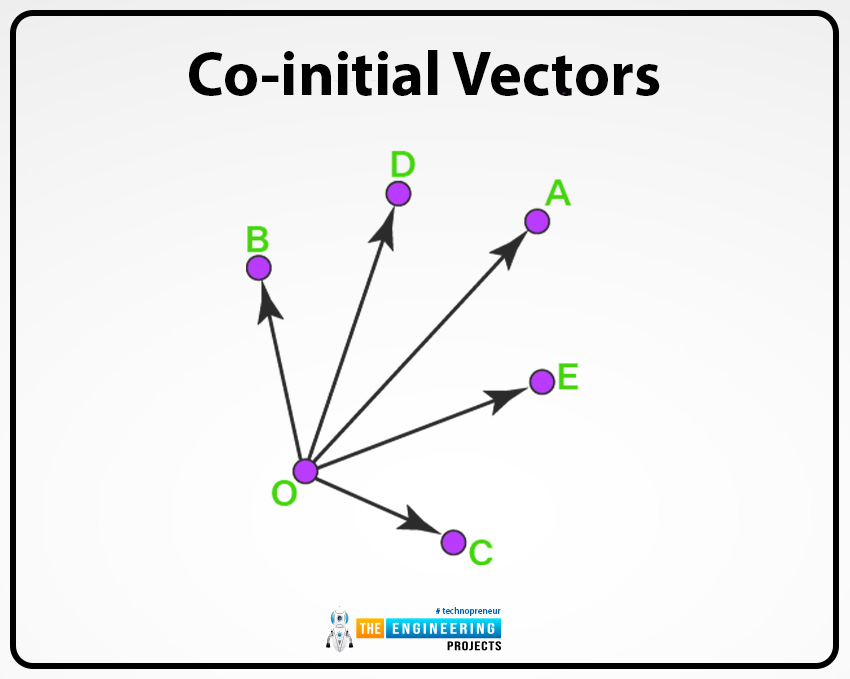
Co-initial vectors:
When two or many vectors have the same origin or initial point on the same plane then it can termed as the co-initial vectors. For example, the vectors A, B and C can originate from the same point with the same plane then it can be called as co initial vector.
Mathematical operations with vectors:
Different mathematical operations with vectors are given below:
Addition of vector
Subtraction of vector
Dot product ( Scalar product)
Scalar multiplication
Cross product (Vector product)
Tip-to-tail rule:
For addition and subtraction of the vector, we can use the tip-to-tail rule in which the tail of the second vector can be placed on the tip of the first vector and the first vector tail is placed on the tip of the second vector.
Addition of a vector:
For the addition of the vector we can use the tip-to-tail rule their mathematical representation is given below;
If we have the vector A their component on x or y is AX and Ay and the other vector B then their component on x and y is Bx and By and their sum is represented by C then they can be added as:
C = A+ B
Then,
A+ B = (Ax + Bx, Ay+ By)
Subtraction of a vector:
Like the addition of a vector, the subtraction of a vector can also follow the head-to-tail rule. so the component method and mathematically expressed equation for the subtraction of a vector are given below:
If we have the vector A their component on x or y is AX and Ay and the other vector B then their component on x and y is Bx and By and their subtraction is represented by C then they can be subtracted as:
C = A– B
Then,
A– B = (Ax – Bx, Ay– By)
Vector product ( cross product):
The cross product is also known as the vector product. In the vector product, the vector A and the vector B are perpendicular to each other then their product in mathematical form can be written as:
A B = ( AyBz– AzBy) i + (AzBx– AxBz) j + ( AxBy – AyBx) k
Magnitude:
The magnitude of the vector or cross product is,
A B = ABsinθ
In this, the sinθ is the angle between the vector A and the vector B.
In physics:
In physics cross products are used to understand the rotational and the circular motion of an object also they can be used to calculate precise calculations like torque.
Scalar multiplication:
When we multiply the vector with the scalar which has only magnitude and these quantities do have not a direction but if the scalar is negative then it means that their direction can be reversed. Their mathematical form is given there,
If we have the vector A and their component on x and y axis is Ax or Ay and the scalar is K then they can be written as:
KA = ( KAX , KAy)
Dot product or scalar product:
The vector A and the vector B, their dot product is the scalar quantity so that's why they are also termed as the scalar product. Their mathematical expression is given below:
A B = AxBx + AyBy + AzBz
Magnitude:
Their product can express their magnitude, not their direction. So the magnitude of the scalar or the dot product is,
A B = AB cosθ
cosθ is the angle between the vector A and the vector B for expressing the magnitude.
In physics:
We can use the scalar and dot product in physics to calculate or determine the angle between the two vectors if one vector is projecting to another vector.
Application of vector quantities in physics:
Vector quantities can play a very essential role in the physics for calculating numerous calculations. Vectors can be used in various fields of physics because by busying the vector mathematical operations we can do very precise and accurate calculations. Now we can discuss some applications of vector quantites in physics. The field of physics in which the vectors are used is given there:
In Mechanics
Newton’s law of motion
Electromagnetism
Maxwell’s equation
Bernoullis equation
Fluid dynamics
Quantum mechanics
Velocity field
Schrodinger equation
Their detail is given there:
Mechanics:
To describe the motion, forces, and displacement in mechanics we can use the vector quantities. Some vector quantities explanation is given there:
Acceleration, displacement, and velocity:
Acceleration: acceleration is the time rate change of velocity, and the vector can express the change of direction and magnitude along with experiencing the quick velocity changing
Displacement: the position which can be changed by the moving object can be expressed by vectors. And the direction with magnitude of these objects can be expressed through vectors.
Velocity: velocity is the rate of change of displacement, their magnitude, direction, and speed can be represented by the vectors.
The equation of motion which can be used in the physics of the vector quantities can also involved in them. For example, the formula for the uniform acceleration is
v = v0 + at
There v expresses the velocity vector, v0 indicates the initial velocity, a is for acceleration and t expresses the time in which the velocity can be changed.
Newton’s law of motion:
In Newton, the law of motion all formulas of Newton's law can be expressed by using vectors. The law of motion with its formula which indicates the magnitude and direction is given there:
The first law of motion: the object always remains at rest unless the external force can act upon it. And through these external forces, the object can be moved.
The second law of motion: the force that can act on the moving object is equal to the mass of an object and also equal to the acceleration. It can be written as F = ma where F is the vector quantity force, m indicates mass and a indicates the acceleration.
The third law of motion: is that every reaction has an equal and opposite reaction it can indicate the magnitude and direction of every action and reaction.
The dynamics of the object, its direction, and magnitude can be expressed through vectors in these equations of motion.
Quantum mechanics:
The vector spaces that can be involved in quantum mechanics are also termed as the Hilbert spaces. The state of particles is represented by the vectors which are used in quantum mechanics and it is also called wavefunction and state vectors. These vectors can also indicate the direction and magnitude of the particles in quantum mechanics.
Fluid dynamics:
In the field of fluid dynamics, the vectors represent the flow of fluid along with their direction and they can also represent the properties of the fluid which can flow. Vectors that can be used in fluid dynamics can also represent their magnitude with properties.
Schrodinger equation:
Schrodinger equation is the time-independent equation. This equation can be described and indicate the quantum state of any physical system independent of time. The vectors which can be used in these equations are written there:
iћ∂∂tψ (r, t) = H ψ ( r, t)
there, ћ expressed the Planck constant, ψ (r,t)expressed the wavefunctions, and the H expressed the Hamilton operator.
Electromagnetism:
In electromagnetism, the vector quantities can expressed and describe the electrical field and the magnetic field. These vectors can also explain the relationship and the interactions of current and the charges in both electrical and magnetic fields.
Electrical field:
The vectors that can be used to express the electric field are;
E = Fq
Where E is the vector that can indicate the electrical field in the space at any point, F is the force that can be experienced by the unit positive charges in the electric field and the q expresses the charges which are present in the electrical field.
Magnetic field:
The vector that expresses the magnetic field and the Lorentz force law is written there:
F = q (v B)
The magnetic field can be expressed through vector B and this vector B can describe the magnetic forces which are present in the magnetic field. The force F experienced by the charges can be expressed by the vector q with the same velocity which can indicated by v.
Bernoulli's equation:
Bernoulli's equation can be derived and dependent on the vector. The vectors which are related in the Bernoullis equation are height, pressure, and velocity in the flowing fluid. The Bernoullis equation formula in which vectors are used is given there:
P + 12 ρv2 + ρgh = constant
There P represents the pressure, ρ represents the fluid density, h represents the height of the fluid according to the reference point, and v represents the fluid velocity.
Maxwells equation:
The electric and magnetic field construction and how these fields can change their current and charges are described through the Maxwell equation. The vectors which can represent these fields current and charges are given there:
Faraday's law of induction:
The vectors that can represent the current and charges in the field are given there:
⛛ E = -∂B∂t
Gauss law for electricity:
The vectors that represent the Gauss law formula for electricity are given there:
⛛ E = pe0
Amperes law:
The vectors that can represent the amperes law formula are given there:
⛛ B = μ0J + μ0ε0∂E∂t
Gauss law for magnetism:
The vectors that can represent the formula of Gauss law for magnetism are given there:
⛛ B = 0
Velocity field:
Fluid particles that are present in space at different points can be explained and described through vectors like v (r,t), and in this v is the vector for velocity, r for the position of the particle, and t is for a time in which the velocity of the particles can be changed and dependent upon the time.
Advanced topics of physics in which vectors are used:
In the modern era of science, vectors can be used in many advanced topics in physics some topics with descriptions are given there:
Tensors
Gradient
curl
Vector calculus
Divergence
Tensors:
The complex physical quantities are also represented and described by the vectors and these vectors which describe complex quantities are generalized, known as tensors. In the continuum mechanics or in the theory of relativity tensors mostly tensors are used.
Gradient:
The vector field gradient is represented by ⛛ and the scalar field gradient is Φ. When the rate of Φ increased then the magnitude rate also increased and this gradient mathematically can be written as:
⛛Φ = (∂Φ∂x , ∂Φ∂y, ∂Φ∂z )
Curl:
The ability and the tendency of the field that can be moved or rotated in a point is termed the curl of the vector field A. Mathematically it can written as:
⛛ A = (∂Az∂y – ∂Ay∂z , ∂Ax∂z – ∂Az∂x, ∂Ay∂x – ∂Ax∂y)
Vector calculus:
The concept of vectors in different fields of physics and mathematics can be extended through vector calculus because we can do different mathematical operations with vectors like curl, gradient, and divergence.
Divergence:
By using the divergence formula we can measure the rate of flow of vectors in the vector field of A. The mathematical expression and the formula of divergence are given below:
⛛ A = ( ∂Ax∂x + ∂Ay∂y + ∂Az∂z )
Conclusion:
In physics, vectors are used as an essential tool because they can provide comprehensive information about the quantity and can also analyze and provide the description of the magnitude and the direction of the quantity in a very efficient way. Mostly it can be used in the field of physics like fluid dynamics, mechanics, electromagnetism, quantum mechanics, and in mathematical operations to derive or express the formula. Vectors can play a very essential role in physics or mathematics. Vectors can become the backbone of calculations in physics or in mathematics because they can help in doing very crucial calculations.