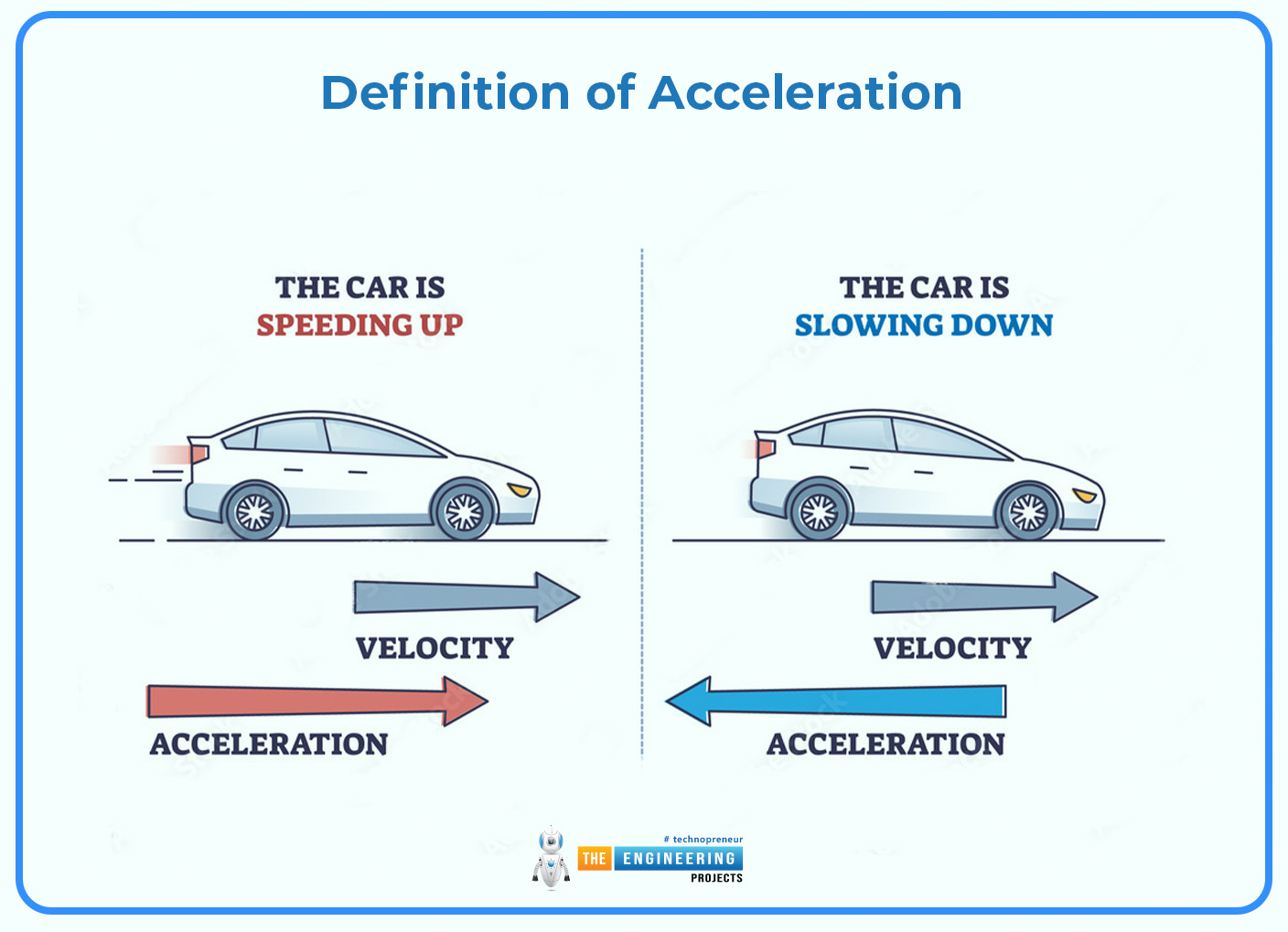
Hi, friends I hope you are all well and doing your best in your fields. Today we can discuss the main topic which is acceleration. Acceleration is a central idea in physics that is key to understanding the motion of objects. It is the rate at which an object changes its velocity with time. This variation can take place either as a change in speed or direction. In simpler words, it tells us how fast the velocity of an object is changing along a particular track. As objects move, they may accelerate by gaining, losing, or changing direction. Many concepts in physics and engineering depend on understanding acceleration, such as the movement of celestial bodies to what happens to everyday objects. It is also vital in explaining why objects move, how forces act on them, and the basic principles governing their motion.
In layman’s language, you can experience acceleration when your car speeds up on a highway when an athlete suddenly changes his/her running direction or even if you throw any ball upwards. By studying the acceleration concept, physicists and engineers can predict and explain motion, design efficient transportation systems, and develop technologies based on controlled motion and velocity changes.
DEFINITION OF ACCELERATION:
Acceleration is simply defined as the rate at which velocity changes in a given period. Velocity is a vector quantity because it has both magnitude and direction; hence, acceleration is also a vector component. The International System of Units (SI) uses meters per second squared (m/s²) as its standard unit of acceleration.
Mathematically, acceleration can be expressed by:
a = Δv/Δt
Where:
∆v( Delta-v ) reflects the change in velocity,
∆t( Delta t ) reflects the change in time.
When an object’s velocity changes uniformly, it undergoes constant acceleration. In contrast, if the rate at which its velocity alters fluctuates, then non-uniform acceleration occurs.
TYPES OF ACCELERATION:
Several types of acceleration can be classified based on their characteristics and context of occurrence:
Uniform Acceleration:
Uniform acceleration is where the rate at which a body’s velocity changes over time remains the same. Such a kind of motion is common in many theoretical studies, making it an easier method to describe motion.
One instance of uniform acceleration is when an object falls freely in a vacuum under gravity with no other forces acting on it. In such a case, it will accelerate downwards due to gravitational pull at approximately 9.8 m/s².
Non-Uniform Acceleration:
Non-uniform acceleration refers to when there are varying velocities during different times. This often takes place in real-life instances whereby various forces may be acting on an object at different times. For example, non-uniform acceleration happens to a car that speeds up and slows down in traffic. Alterations in the forces exerted on this vehicle (like gear position or road conditions) make for fluctuations in its rate of change of speed.
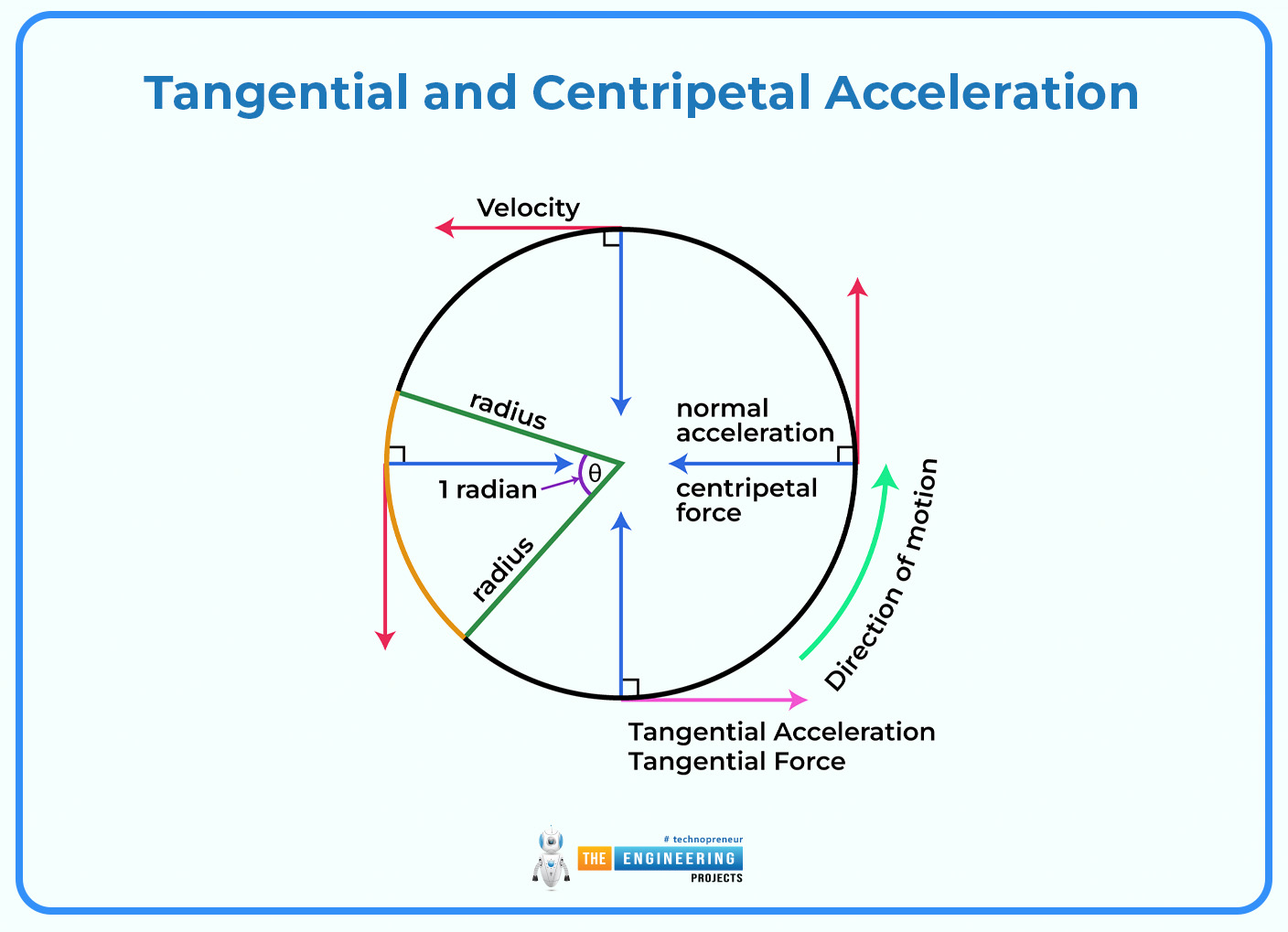
Tangential and Centripetal Acceleration:
In circular motion, there are two components of acceleration: tangential and centripetal. Tangential acceleration occurs whenever there is a change in speed along any point around the circumference. Tangential acceleration is experienced when there is an alteration in the speed along the circular path. On the other hand, centripetal acceleration points towards the center of a circle and helps to keep the object on its curved course. The formula for centripetal acceleration ac can be given as:
ac = v2/r
Where:
( v ) is the velocity of the object along the circular path,
( r ) is the circle’s radius.
Alternatively, in terms of angular velocity (ω) and radius ( r ), we can also write centripetal acceleration:
ac = r ω²
This implies that centripetal acceleration will always point to the center of a circular path and is responsible for altering the direction of an object’s velocity without affecting its magnitude (speed). This concept is important in understanding circular motion because it is related to the force-directed inward that keeps objects following curved paths, which are shown by Newton’s laws of motion.
In physics, tangential acceleration refers to how fast an object’s rate or speed changes as it travels along a curved path. Unlike linear acceleration, which varies an object’s speed on a straight trajectory, tangential acceleration affects the speed of an item moving along a bent direction.
In rotational movement or while an item actions alongside a round route, its pace modifications no longer only in significance but additionally in the course. Tangential acceleration (at) in particular refers back to the factor of acceleration that causes modifications in the pace (importance of speed) of the item. It is directed along the tangent to the route of motion and is measured in meters in line with second squared (m/s²).
Mathematically, tangential acceleration can be expressed as:
At = d|v| /dt
Where |v| denotes the magnitude of the velocity vector v.
Tangential acceleration plays a vital function in expertise round and rotational movement. For instance, whilst an automobile negotiates a curve on a tune, its speed adjustments are not handiest due to speed changes (tangential acceleration) but additionally due to changes in the path (centripetal acceleration). Together, these accelerations determine how easily and predictably an object can navigate curves without skidding or losing manipulation.
In precis, tangential acceleration describes how the speed of an item adjusts along a curved path, offering crucial insights into the dynamics of rotational and round motion in physics.
Centripetal acceleration is the acceleration that continues an item transferring in a circular route. It is directed in the direction of the center of the circle or the axis of rotation, perpendicular to the item’s velocity vector. In many sensible situations, centripetal acceleration arises while an item moves alongside a circular trajectory, together with a car navigating a curve, a planet orbiting a celebrity, or a satellite TV for pc circling the Earth.
Centripetal acceleration is continually directed toward the center of the round course and is chargeable for converting the route of an item’s pace without altering its velocity (value of speed). It is a vital idea in information circular movement and is carefully related to the centripetal pressure required to preserve the object’s round path, as described with the aid of Newton’s laws of motion.
In summary, centripetal acceleration is the acceleration that acts toward the center of a round direction, making sure that gadgets preserve their trajectory and do now not deviate into an instant line.
MATHEMATICAL REPRESENTATION OF ACCELERATION:
The mathematical representation of acceleration can be explored through various equations and principles, often linked to Newton’s laws of motion.
Kinematic Equations:
For motion with uniform (constant) acceleration, we use a set of kinematic equations to describe the relationships between displacement (s), initial velocity (u), final velocity (v), acceleration (a), and time (t). These equations are fundamental in classical mechanics and are used to solve various problems involving motion.
Final Velocity Equation:
v = u + at
According to this equation, the final velocity (v) is equal to the initial velocity (u) plus the product of acceleration (a) and time (t).
Displacement Equation:
s = ut + ½ at²
This equation provides the displacement (s) of an object based on its initial velocity (u), time (t), and acceleration (a).
Velocity-Displacement Equation:
v² = u² + 2as
This equation relates the final velocity (v), initial velocity (u), acceleration (a), and displacement (s). It is especially helpful in situations when time is unknown.
These kinematic equations assume constant acceleration and are widely used in physics to analyze the motion of objects.
Newton's Second Law of Motion:
Classical mechanics is based on Newton’s second law of motion. Establishes the relationship between force (F), mass (m), and acceleration (a);
F = ma
This equation shows that the force acting on an object is equal to the product of its mass and velocity. It means that the velocity of an object is inversely proportional to its mass and directly proportional to the applied force. This principle is important for understanding how forces affect processes.
For example, if a net force is applied to a car, its acceleration can be determined by dividing the force by the weight of the car. Conversely, the required force can be calculated by determining the desired magnitude and velocity.
Centripetal Acceleration in Circular Motion:
When an object acts in a circular direction, it experiences centripetal acceleration, which is directed toward the center of the circle. This acceleration is essential to trade the direction of the item's speed, keeping it on the circular course. The following yields the centripetal acceleration (ac ) ;
ac = v²/r
where:
(v) is the velocity of the object along the circular path,
(r) is the circle’s radius.
This equation suggests that centripetal acceleration increases with the square of the velocity and reduces with an increase inside the radius of the circular course. It is crucial for understanding the dynamics of items in circular motion, like cars taking a turn or planets orbiting the Sun.
Example:
Suppose a car traveling at a speed of 20 m/s around a curve with a radius of 50 meters. The centripetal acceleration ( ac ) Can be calculated using the formula:
ac = v²/ r
ac = 20²/ 50
ac = 400/50
ac = 8m/s²
The car exploits a centripetal acceleration of 8 m/s² in the direction of the circular path’s center.
Differential Form of Acceleration:
In calculus, acceleration can be expressed as the derivative (d) of velocity concerning time. If velocity (v) is a function of time (t), then acceleration (a) is given by:
a = d v / dt
This differential form provides a precise way to describe acceleration at any given instant. For cases where velocity is not constant, integrating acceleration over time can determine the change in velocity;
v = ∫a dt
Similarly, if acceleration itself is a function of time, position, or velocity, the motion of the object can be analyzed using differential equations. Solving these equations yields detailed information about the object's velocity and position over time.
Gravitational Acceleration:
In particular, the uniform acceleration with which the bodies falling freely near the Earth’s surface act is called gravitational acceleration or Gravitational acceleration is the acceleration associated with the force of gravity of a body, for example, the Earth. Estimates put it at 9. 8 m/s² and this is abbreviated as ‘g’. The equations of motions for objects under gravitational acceleration are as follows; very much like kinematical equations, the only changes that occur is the use of (a) as (g).
For an object in free fall, the equations become:
Final velocity: v = u + gt
Displacement: s = ut + ½ gt²
Velocity-displacement: v² = u² + 2gs
These equations are very useful for solving problems on the motion of objects under the force of gravity like a falling object or a projectile.
Gravity acceleration is simply the acceleration that an object goes through when under the effect of gravity. On the surface of the earth, the acceleration due to gravity is roughly about 9. 81 meters per second squared ( 9. 81 m/s² ). This value gives the rate at which objects fall towards the center of the earth because of the force of gravity.
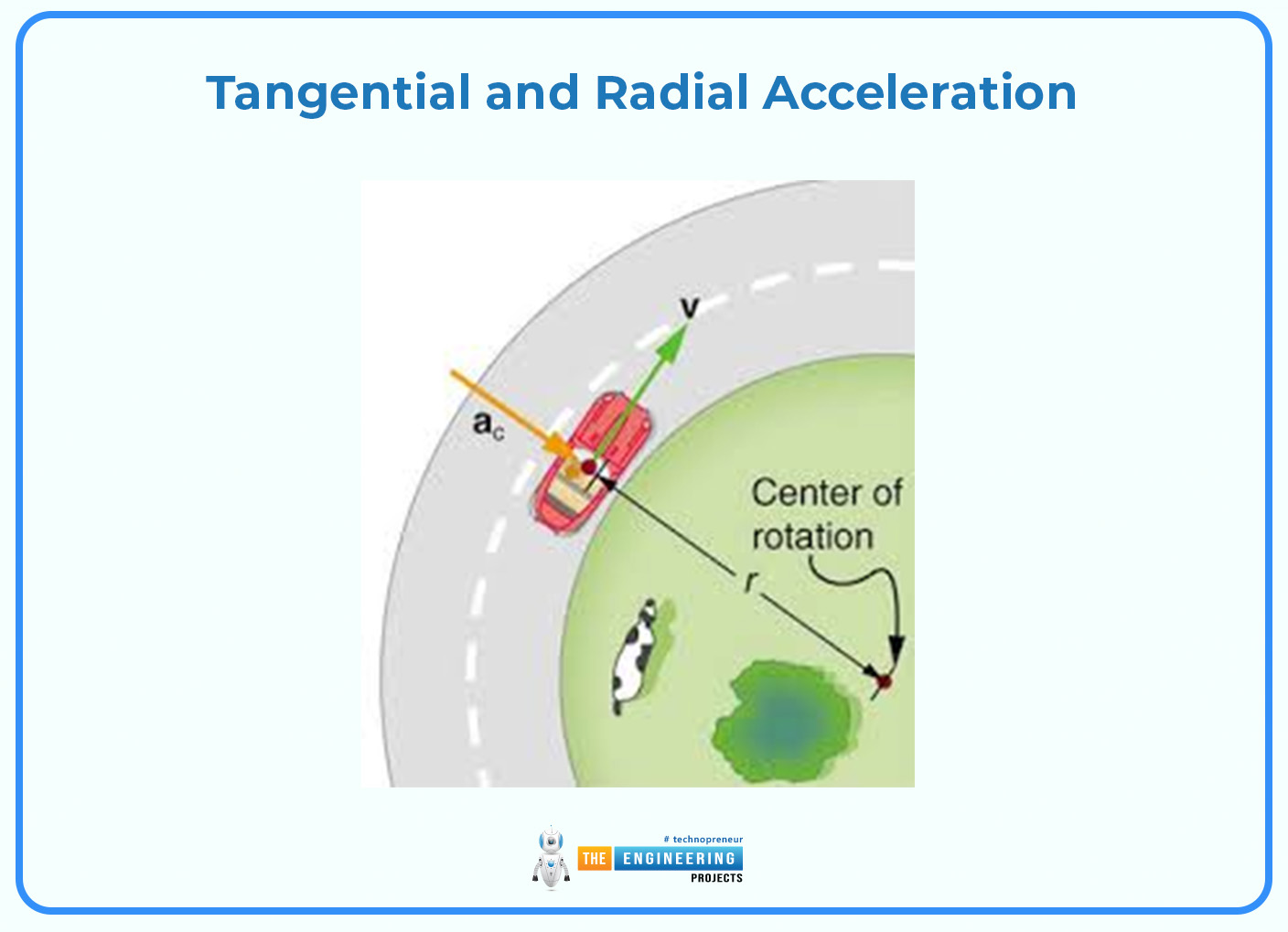
Tangential and Radial Acceleration:
Of the two types of acceleration, the tangential acceleration deals with acceleration in the plane of motion or along the circle’s circumference while radial acceleration refers to the acceleration that is directed toward or away from the center of the circle. Tangential acceleration (at) is an acceleration in the radial direction it is incorporated into the change speed of the object in the circular path and radial or centripetal acceleration (ar) is towards the center to reverse the direction of the velocity vector head.
If the angular velocity (ω) of an object in circular motion changes over time, the tangential acceleration can be expressed as
If the angular velocity (ω) of an object in circular motion changes over time, the tangential acceleration can be expressed as:
at = r dω/ dt
where (r) is the radius of the circular path.
The total acceleration (a) is the vector sum of tangential and radial acceleration which is represented by The mathematical formula for the same is;
a = √at² + ar²
These components are significant in analyzing objects in a non-uniform circular motion because it is applicable in real-life situations like cars moving at different speeds on curves.
Summary:
Concluding, it is necessary to state that acceleration in mathematics is described by several equations and principles that determine the change of velocity in an object throughout time. Some of them are the kinematics equation for the impact of uniform acceleration, Newton’s second law, centripetal acceleration for circular motion, differential calculus for non-uniform acceleration, specific instances like gravitational acceleration, and so on. For students, these tools are indispensable necessities for finding solutions to various problems and for understanding the motion of various objects in situations of their application.
MEASURING ACCELERATION:
ACCELEROMETERS:
Accelerometers are therefore instruments that are used in the measurement of acceleration. It is used in almost every technological field; right from mobile phones to space shuttles. Accelerometers work based on the principle that they generate an electrical signal that is proportional to the force exerted on a test mass in the device under the effect of acceleration. Below are some of the common types of accelerometers;
Capacitive Accelerometers:
These measure changes in capacitance due to the displacement of a test mass when acceleration happens. capacitive accelerometer is a kind of accelerometer which its
working is based on capacitance change as a result of acceleration.
Capacitive accelerometers refer to the devices that are commonly used in the measurement of acceleration through capacitance variations. They consist of two main components: a proof mass and a fixed capacitor structure is used. The proof mass is often, but not necessarily, small and is free to move in a direction perpendicular to the direction of the force being measured by the interferometer, and is attached between two springs. As the accelerometer goes through acceleration, the proof mass shifts concerning the fixed plates of the capacitor and results to a change in capacitance.
Based on the above results, it can be noted that the change in capacitance is directly proportional to the acceleration applied to the device. This can be measured electronically and converted into an acceleration value depending on calibration value and signal processing measures.
The above capacitive accelerometers' main characteristics and benefits are high sensitivity, low power consumption as well as an extended measurement range. They are popular in many demands for the measurement of acceleration including automotive technology (For example air-bag systems), aerospace engineering (For instance, flight control), handheld devices (For instance, the built-in accelerometer in every smartphone for tilting), and large machinery (For instance vibration measuring).
Piezoelectric Accelerometers:
These produce an electric charge as a result of mechanical stress from acceleration. A piezoelectric accelerometer, as a kind of accelerometer, is an instrument that can define acceleration by using the piezoelectric phenomenon.
Piezoelectric accelerometers are devices used to measure accelerations, vibrations, and shocks for many applications. They use the working of piezoelectric effect which states that acceleration is transformed into electrical charge. These accelerometers include a piezoelectric crystal, usually of quartz or ceramic, whose output voltage depends on the acceleration.
The important characteristics of piezoelectric accelerometers are high or greater sensitivity, wide frequency range, robust structure, and insensitivity to high temperatures. These applications are in automobile manufacturing, aerospace, manufacturing industries, and in the monitoring of structures.
How piezoelectric accelerometers work?
Piezoelectric Crystal: The principal part of a piezoelectric accelerometer is a piezoelectric crystal with quartz or ceramic material. When the accelerometer does move and thus, apply inertial force on it, then, the crystal elongates or contracts slightly.
Generation of Electrical Charge: As per the piezoelectric effect, the above-mentioned deformation results in the formation of an electrical charge on the surface of the crystal. The degree of charge is proportional to the acceleration applied to the accelerometer device.
Measurement and Output: The generated electrical charge is usually intensified and analyzed through the use of electronics within the accelerometer. This leads to an output signal (generally voltage) proportional to the acceleration that the device is subjected to.
Piezoelectric accelerometers are provided in several formats and orientations single, dual, and triaxial depending on the utilization of the device. They are widely applied for vibration measurement in rotating and other machinery, structure monitoring, automotive safety by crash testing, and seismic application.
MEMS Accelerometers:
MEMS accelerometers are small-size, low-cost acceleration sensors commonly used in portable electronics. They employ minuscule mechanical elements that bend with acceleration and change the various electrical currents. MEMS accelerometers are electrical devices that are quite small and are employed for measuring accelerations.
MEMS accelerometers as small, integrated devices that measure acceleration using microfabrication technology. They can be classified into the family of micro-electromechanical system sensors, often abbreviated as MEMS, where mechanical components include springs and proof masses as well as electronic components like capacitors and resistors and are all integrated into one chip.
How do MEMS accelerometers work?
Microfabricated Structure: Generally the MEMS accelerometers have a micro-fabricated structure; in most common configurations there is a proof mass that is attached to the substrate by springs. The proof mass is displaced relative to the package frame under the action of external forces that cause acceleration.
Sensing Principle: Acceleration leads to forces on the proof mass causing it to move a certain distance away from the springs. This displacement is measured with several sensors, for example, capacitive sensors or piezoresistive sensors.
Signal Processing: Due to this movement of the proof mass an electrical signal corresponding to the acceleration is obtained. The signal is then amplified by integrated electronics which are provided in the specific MEMS chip to generate a readable output.
There are different types of MEMS accelerometers and they can be classified based on their axis; they can have single-axis, two-axes, or three-axes. They are used in a wide range of applications, including:
Consumer Electronics: Smartphones and tablets motion sensing, and gaming control equipment.
Automotive: Airbag: active and passive electronic systems concerning vehicle stability, and vehicle navigation systems.
Industrial: Machinery condition monitoring, attitude determination and control, and structure health monitoring.
Healthcare: Including fall detection gadgets, wearable health monitors, and health enhancers in the human body.
ADVANCED CONCEPTS IN ACCELERATION:
RELATIVISTIC ACCELERATION:
In the realm of special relativity, the concept of acceleration becomes more complex. As objects approach the speed of light, their mass effectively increases, requiring greater force to achieve further acceleration. The relativistic form of Newton's second law is used to account for these effects:
F = γ³ma
where:
γ is the Lorentz factor, given by ;
v is the velocity of the object,
c is the speed of light.
This equation shows that as v approaches c, γ increases significantly, making it increasingly difficult to accelerate the object further.
GRAVITATIONAL ACCELERATION IN GENERAL RELATIVITY:
In general relativity, acceleration due to gravity is understood as the curvature of space-time caused by massive objects. Instead of viewing gravity as a force, general relativity describes it as the effect of space-time curvature on the motion of objects. The equations governing this curvature are given by Einstein's field equations:
Gμν = 8πG/c⁴ Tμν
where:
Gμν is the Einstein tensor representing space-time curvature,
G is the gravitational constant,
c is the speed of light,
Tμν is the stress-energy tensor representing matter and energy distribution.
In this framework, objects follow geodesics, which are the paths determined by the curvature of space-time. The acceleration of objects in a gravitational field is thus a manifestation of their motion along these curved paths.
PRACTICAL APPLICATIONS OF ACCELERATION IN TECHNOLOGY:
AEROSPACE ENGINEERING:
In aerospace engineering, understanding acceleration is crucial for designing aircraft and spacecraft. Engineers must consider the accelerations experienced during various phases of flight, including take-off, cruising, maneuvering, and landing.
AIRCRAFT DESIGN:
During the design of aircraft, engineers analyze the accelerations and forces acting on the airframe to ensure structural integrity and passenger comfort. This involves studying the effects of aerodynamic forces, thrust, and gravitational forces. Pilots also need to understand acceleration to perform safe and efficient maneuvers.
SPACECRAFT NAVIGATION:
Spacecraft navigation relies heavily on precise calculations of acceleration. For example, during interplanetary missions, spacecraft use gravity assists (also known as gravitational slingshots) to change their trajectories and speeds. By carefully planning these maneuvers, mission planners can use the gravitational fields of planets to accelerate the spacecraft, saving fuel and reducing travel time.
AUTOMOTIVE ENGINEERING:
In the automotive industry, acceleration is a key factor in vehicle performance, safety, and comfort. Engineers use the principles of acceleration to design better engines, braking systems, and suspension systems.
ENGINE PERFORMANCE:
The performance of a car engine is often measured by its ability to accelerate the vehicle. Engineers design engines to provide optimal acceleration while maintaining fuel efficiency and reducing emissions. This involves optimizing the combustion process, transmission system, and overall vehicle weight.
SAFETY SYSTEMS:
Modern cars are equipped with advanced safety systems that rely on precise measurements of acceleration. For example, electronic stability control (ESC) systems use accelerometers to detect and correct skids or loss of control. Similarly, airbag deployment systems use accelerometers to detect sudden decelerations during collisions and deploy airbags to protect occupants.
ROBOTICS:
In robotics, controlling acceleration is essential for achieving precise and efficient movements. Robots in manufacturing, healthcare, and exploration require accurate acceleration control to perform tasks effectively.
INDUSTRIAL ROBOTS:
Industrial robots often operate in environments that require high precision and speed. To achieve this, robots use advanced control algorithms to manage acceleration and deceleration smoothly. This helps prevent mechanical wear and tear and ensures accurate positioning.
MEDICAL ROBOTS:
Medical robots, such as surgical robots, must operate with high precision to perform delicate procedures. Controlling acceleration in these robots is critical to avoid damaging tissues and to provide smooth and controlled movements.
MEASURING AND ANALYZING ACCELERATION:
EXPERIMENTAL TECHNIQUES:
Various experimental techniques are used to measure and analyze acceleration in different contexts. These techniques range from simple mechanical setups to advanced electronic systems.
Pendulum Experiments:
One of the simplest ways to study acceleration is through pendulum experiments. By measuring the period of a pendulum's swing, one can calculate the acceleration due to gravity. For the simple pendulum, The period (T) is written as:
T = 2π √L/g
where:
( L ) is the pendulum’s length,
and ( g ) is the acceleration caused by gravity.
By measuring (T) and (L), the value of (g) can be determined.
Drop Tower Experiments:
Drop tower experiments involve dropping an object from a known height and measuring its acceleration as it falls. These experiments are often used to study the effects of microgravity and to test the performance of accelerometers. The object's acceleration can be analyzed using high-speed cameras or precise timing systems.
Computational Methods:
Computational methods, including numerical simulations and modeling, are used to study complex systems where analytical solutions are not feasible.
Finite Element Analysis (FEA):
Finite element analysis (FEA) is a computational technique used to simulate and analyze the behavior of structures under various loads, including acceleration. FEA divides a structure into smaller elements and solves the equations of motion for each element. This method is widely used in engineering to predict the performance of complex systems.
Computational Fluid Dynamics (CFD):
In fluid dynamics, acceleration plays a critical role in the behavior of fluids. Computational fluid dynamics (CFD) is used to simulate the motion of fluids and the forces acting on them. By solving the Navier-Stokes equations, CFD can provide detailed insights into the acceleration of fluid particles and the resulting flow patterns.
CONCLUSION:
Acceleration is a vital idea in physics that narrates how the object’s velocity varies over time. It is essential for understanding the dynamics of motion and has a wide range of applications in everyday life, engineering, technology, space exploration, and scientific research.
From the uniform acceleration of free-falling objects to the complex accelerations experienced by spacecraft, the study of acceleration provides insights into the forces and interactions that shape our world. By employing mathematical equations, experimental techniques, and computational methods, scientists and engineers can analyze and predict the behavior of systems under various conditions of acceleration. Understanding acceleration not only helps us comprehend the physical world but also drives technological advancements and innovations that improve our lives.