Hello friends, I hope you are all well and doing good in your fields. In the previous article, we can discuss the distance and displacement of the objects. Still, today we can talk about velocity because velocity provides information about the speed from which the object can be displaced from one point to the other point. Everything can be moved from one place to another with different speeds and velocities. To understand the speed or the motion of an object it is compulsory to understand the velocity. The concept of velocity is the cornerstone notion in the field of physics because it can provide information about the rate of change of displacement or position. Through speed and velocity, the object can be displaced but the speed is a scalar quantity because it can only provide the magnitude but the velocity is the vector quantity which can provide both magnitude and direction.
In dynamics, and kinematics it can play a very crucial role in understanding the motion of the displaced objects and also helps to understand the various physical phenomena related to the motion of an object. Simply speed and velocity are a combination but speed only provides the magnitude while velocity provides both the magnitude and direction of the moving object. Like kinematics, the notion of velocity is fundamental to understanding the motion of an object in mechanics.
Both speed and velocity describe the motion of an object, based on the idea that an object can be moved fast or slow. Speed and velocity help to identify the objects that can be moved fast or also those objects that can be moved slow. When two objects are displaced at the same time, the fastest object can reach its ending point and this object has high speed and velocity as compared to others. Now, we can start exploring the basic definition of velocity, its types, mathematical representation, examples, and the main difference between speed and velocity.

Definition of velocity:
Velocity is defined as:
“The rate of the change of the position of the body with time or the rate of the change of displacement with time is termed as velocity.”
The main difference between speed and velocity is that speed is the rate of change of position in the unit of time but velocity is the rate of change of displacement in the unit of time.
Mathematical representation:
Mathematical representations of velocity are written below:
Velocity = displacement x time
v =dt
there,
v represented velocity and d represented displacement and t represented the time.
This formula can also be written as:
d = vt
This formula shows that the body can be displaced with some velocity at the unit time.
SI unit:
The SI unit of the velocity is the same as the speed which is meter per second and is written as ms (ms-1).
Dimension:
Dimension of velocity SI unit are written below:
ms-1 = LT-1
There, L is the dimension for m and T-1 is dimension or s-1.
Average velocity:
Average velocity can be defined as:
“ the ratio of the total change of position or displacement with the total time taken is termed as average velocity”
generally, the average velocity is the overall motion of the object that can be covered from one place to another with a unit of time.
Mathematical representation:
Average velocity can be mathematically represented as:
vav = ΔdΔt
There, v represented the average velocity, Δd represented the rate of change in displacement and Δt represented the rate of change in time.
SI unit:
The SI unit of the average velocity is a meter per second and is written as ms (ms-1)
Dimension:
Dimension of average velocity SI unit are written below:
ms-1 = LT-1
There, L is the dimension for m and T-1 is dimension or s-1.
Direction:
The direction of the average velocity of the displaced object is always in the direction of the displacement.
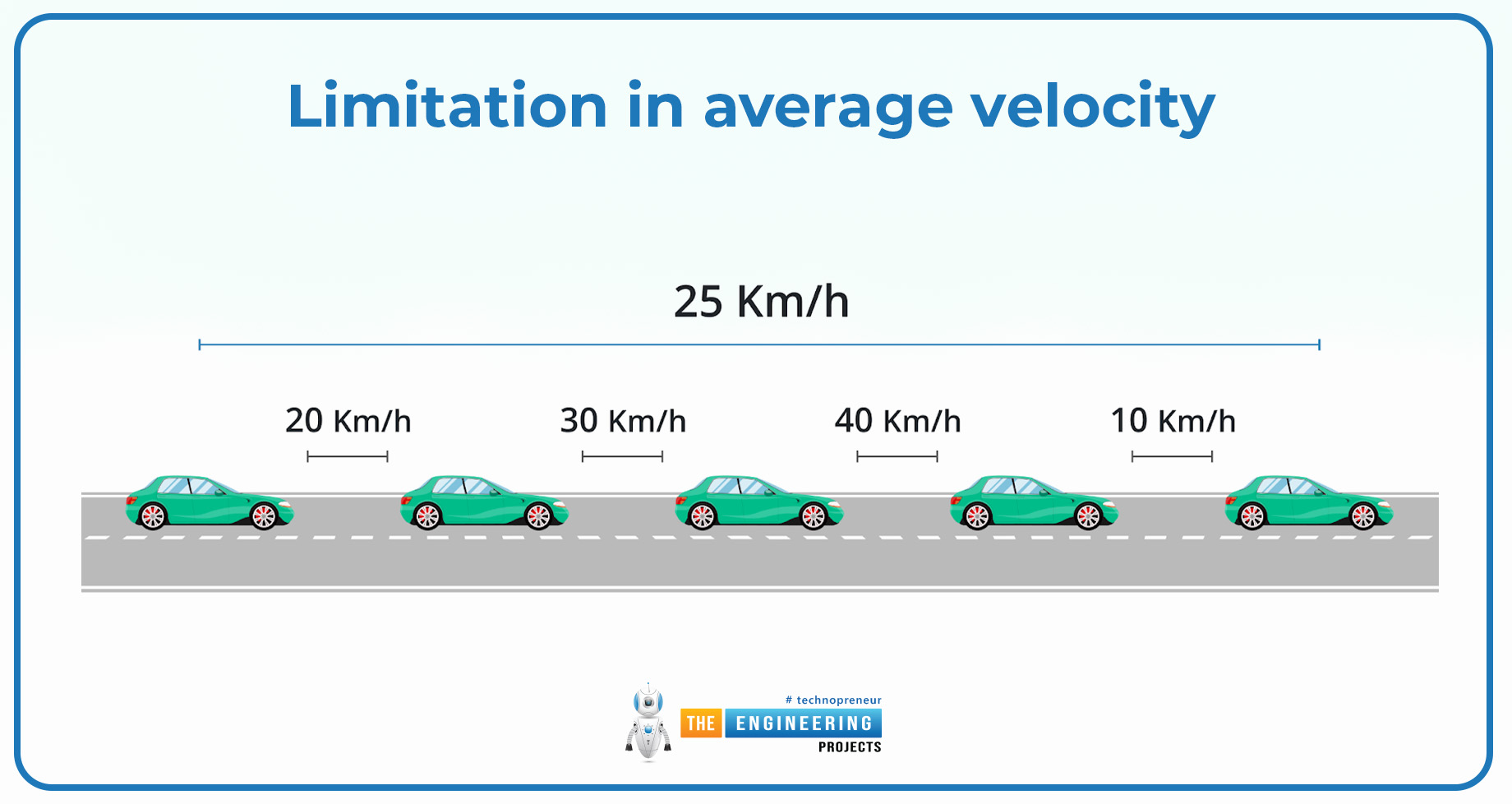
Limitation in average velocity:
Some major limitations of the average velocity are given there:
Average velocity can't describe the motion of the object or body, the body or object may be do random motion or maybe it can do a steady motion. But the average can't tell about their type of motion.
Average velocity can't also provide information about the path in which the body can be displaced because the path may be curved or it may be straight.
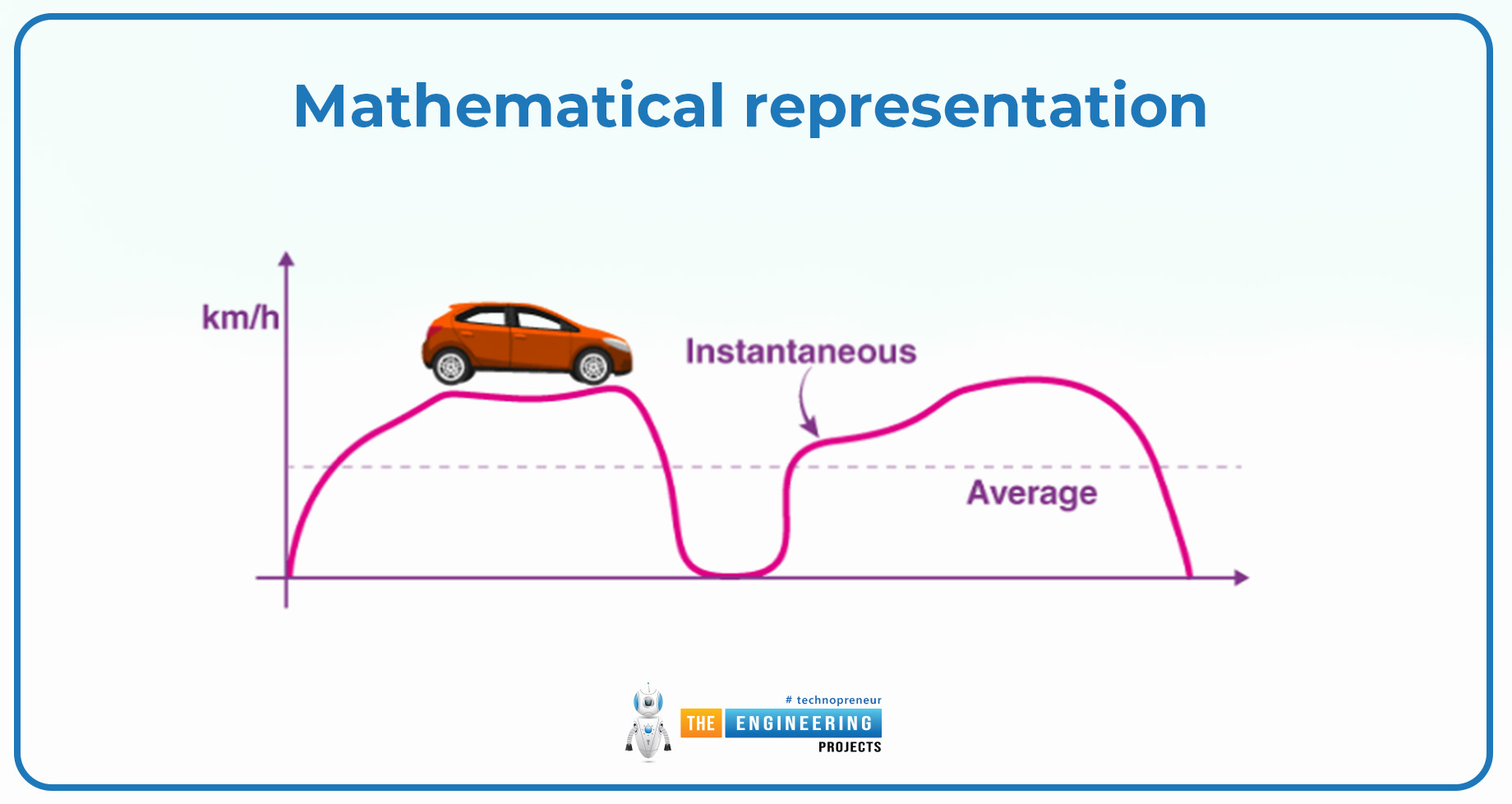
Instantaneous velocity:
Instantaneous velocity can be defined as:
“The instantaneous velocity of the object is the limit or average velocity interval with a change in the time and the velocity reached at zero.”
the instantaneous velocity is the velocity of the moving object at some special or specific point or moment. Instantaneous velocity can be derived when we take the average velocity at a specific time.
Mathematical representation:
The mathematical representation of the instantaneous velocity is written below:
vins = Δt0ΔdΔt
There, vins represented the instantaneous velocity, Δt0represented the average limit of the velocity with time, and reached zero, Δd the rate of change of displacement, and Δt represented the rate of change in time.
The formula of the instantaneous velocity can also be written as:
s = v dt
There, s represented the displacement function, v represented the velocity, d represented the displacement of the displaced object and t represented the time in which the body can be displaced.

SI unit:
The SI unit of the instantaneous velocity is the same as the velocity or the average velocity which is a meter per second and is written as ms (ms-1)
Dimension:
Dimension of instantaneous velocity SI unit is written below:
ms-1 = LT-1
There, L is the dimension for m and T-1 is dimension or s-1.
Direction:
The direction of the instantaneous velocity of the displaced object is always in the direction of the displacement.
Important point:
The instantaneous velocity of the moving body can't equal zero but the average velocity of the moving body or the object may be equal to zero.
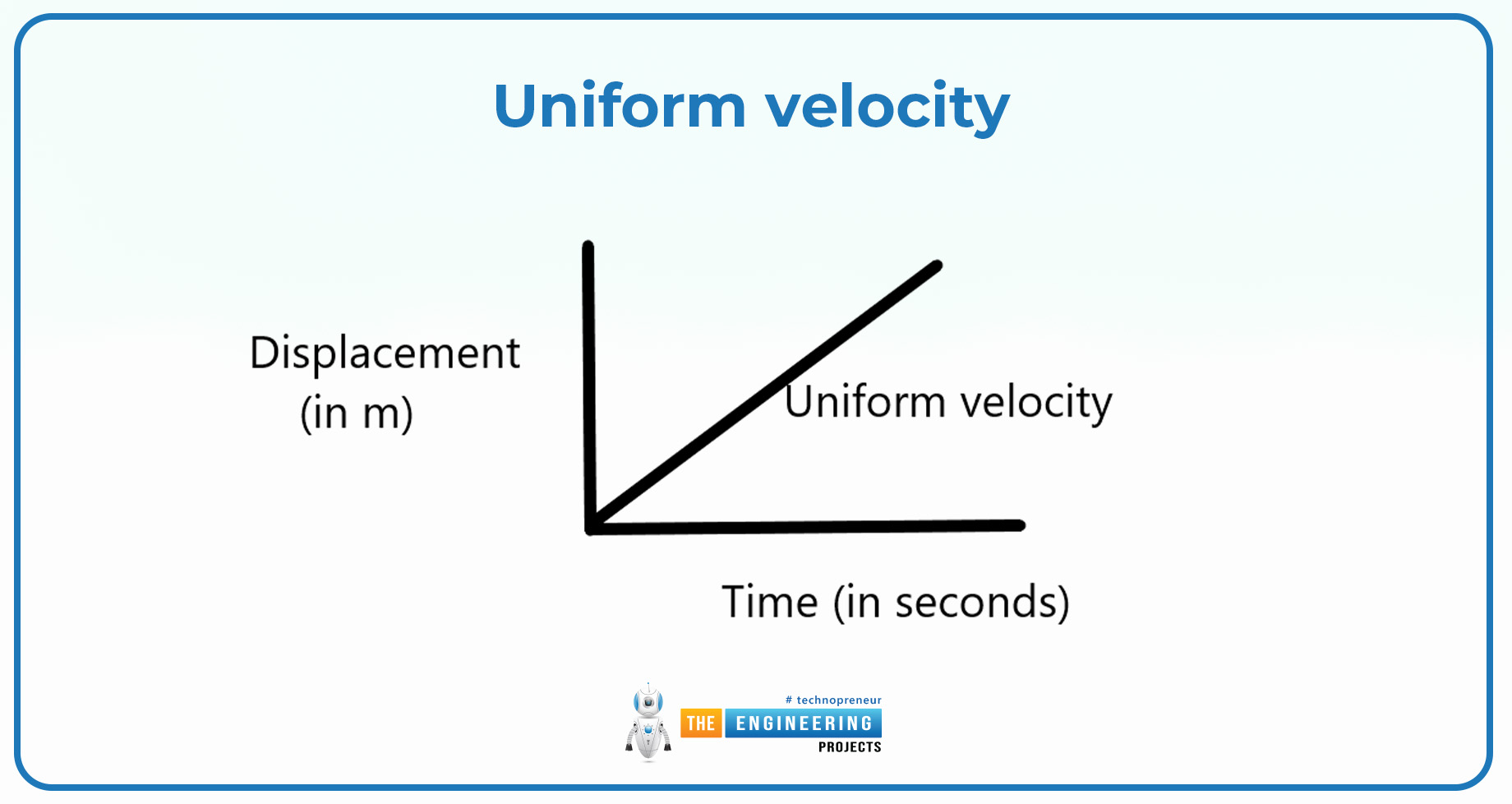
Uniform velocity;
Uniform velocity can be defined as:
“The body that can cover the displacement is equal to the time intervals and moves constantly without changing the displacement in unit time.”
The body can be moved with a uniform velocity when it can cover the displacement, the displacement is equal to the time interval and they are constantly moved.
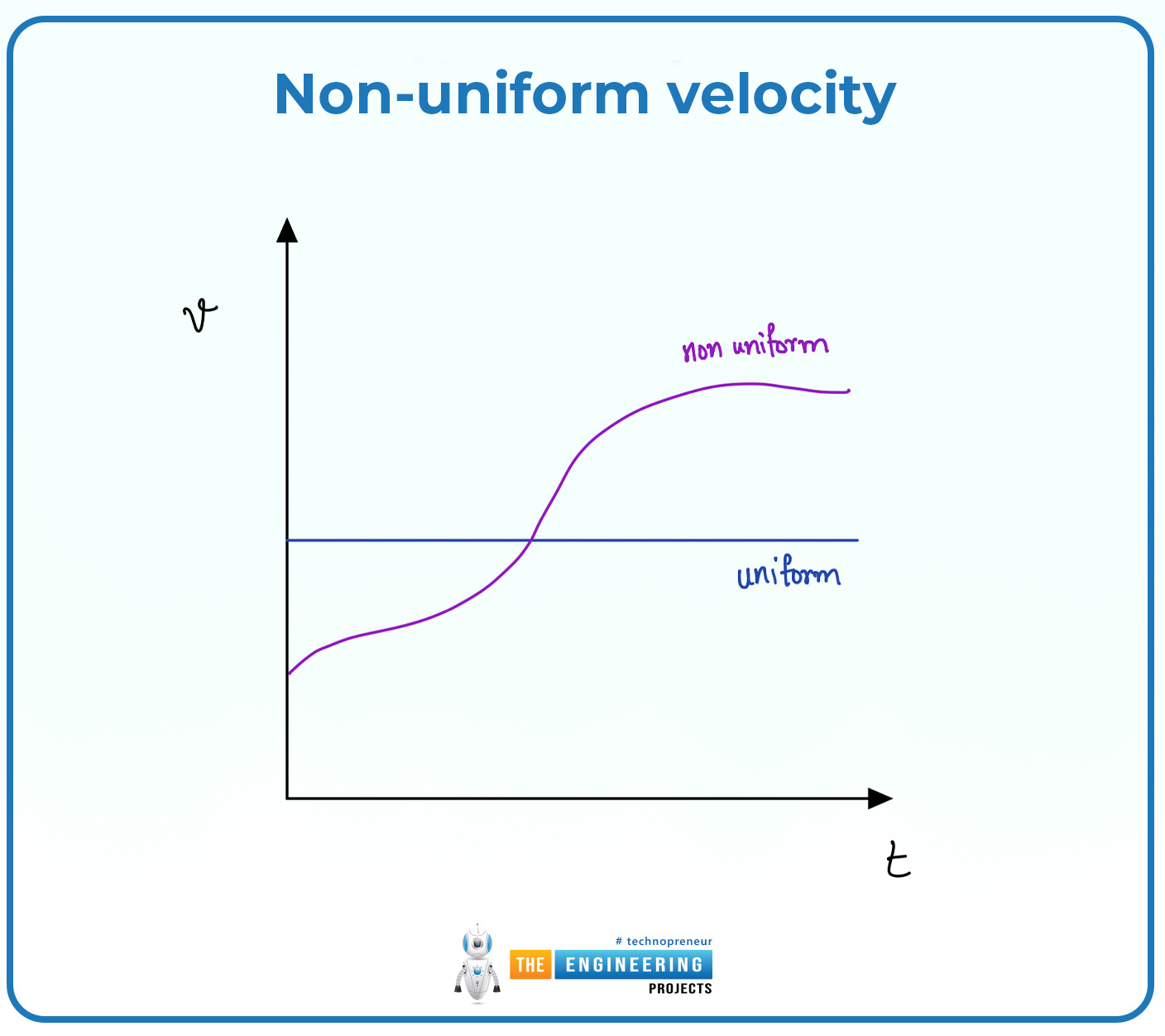
Non-uniform velocity:
Non-uniform velocity can be defined as:
"The body that can cover the unequal displacement is equal to the time intervals and moves constantly with changing the displacement in unit time."
Some other units of velocity:
Some other units of velocity rather than meters per second are mph or fts-1These two units are also commonly used.
Uniform velocity of some particles in some special cases:
Many different particles can be moved or displaced at the same time with uniform velocity in many different special cases but in these cases, the particles moved with uniform velocity with different time intervals such as v1t1, v2t2, ………. vntn. then we can find the average velocity by using the given formula.
v = v1t1 + v2t2 + v3t3 +v4t4........... + vntnt1 + t2 + t3 +t4........ + tn
Then, we know that t1+ t2 + t3+ …… + tn = t
Now we use the arithmetic mean for the average speed and write as:
v =v1 + v2+ v3 +v4........... + vnn
Also written as:
v = 1n i=1nvi
But when the particles can be displaced with different or numerous distances with equal intervals of time and also with the same distance then it can be written as:
v = s1+ s2 + s3 + s4...... snt1 + t2 + t3 +t4........ + tn
It can also be written as:
v = s1+ s2 + s3 + s4...... sns1v1 + s2v2 + s3v3 + s4v4+ ......+ snvn
In the average speed, we can use the arithmetic mean but when the particles cover different distances then it can be equal to the harmonic mean and it can be written as:
v = n (1v1 + 1v2 + 1v3 + 1v4 + ……. + 1vn)-1
And then according to harmonic mean, it can be written as:
v = n (i=1n1vi)-1
Different quantities that can be depend upon the velocity:
Some different quantities which can be depended upon the velocity are given there:
Drag force
Momentum
Escape velocity
Kinetic energy
Lorentz factor
Their description is given there:
Drag force:
Drag forces are the fundamental concept to understand for understanding the motion of fluid or in fluid dynamics because drag force is the specific force that can act opposite to the object's motion because the body or object can be moved in the fluid so this force helps to move in the fluid in the right direction. The formula for drag force is vine there:
FD = 12 ρ v2 CDA
According to the given formula, it can be shown that the drag force is dependent upon the square of the velocity.
There,
FD represented the drag force in fluid dynamics.
Ρ represented the momentum of the moving object.
v2 is the square of the velocity.
CD is the coefficient of the drag force.
A represents the area in which the drag force or the body can be moved.
Momentum:
The momentum of the body can also depend upon the velocity directly because according to the second law of Newton, the momentum of the body or object is equal to the product of mass and velocity and it can be written as:
ρ = mv
There,
ρ represented the momentum
M represents the mass of the object or body
v represented the velocity of the object through which it can be moved or displaced.
Escape velocity:
Simply, escape velocity is the velocity of an object to escape from the earth moon or other massive bodies. Through the escape velocity, the rockets can reach space. The general formula that can describe the velocity is given there:
ve = 2GMr
There,
ve represented the escape velocity.
G represented that gravitational force and its value are fixed.
M represented the mass of the object or body
r represented the radius of the body from Earth.
The above formula can also be written as:
ve = 2gr
Kinetic energy:
Kinetic energy can also depend upon the velocity directly and the formula that can show this is given there:
Ek = 12 mv2
There,
Ek represented the kinetic energy.
m represented the mass of the object or body
v represented the velocity and kinetic energy was directly dependent upon the square of the velocity.
Lorentz factor:
In the formula of special relativity of the Lorentz factor, the Lorentz factor depends upon the velocity, and the formula is written there:
🇾 = 11- v2c2
There,
γ represented the Lorentz factor.
V represented the velocity on which the Lorentz factor depends.
c is the speed of light.
Velocities in the scalar quantities:
When the velocity of the object or the moving body occurs in one dimension, then their velocity is always scalar and it can be written as:
v = v - (-w)
When the two objects can be moved in the same direction the equation can be written like this. But if the two objects are not moved or displaced in the same direction and move in opposite directions then it can be written as:
v = v - (+w)
Equation of motion:
In the equation of motion velocity is the main integral because through the velocity we can understand the motion of the numerous displaced objects when different forces act upon that. The equation of motions in which the velocity relationship is shown is written below in detail.
The first equation of motion
The second equation of motion
Third equation of motion
The first equation of motion:
The formula of the first equation of motion in which the velocity relation can be shown is given there:
v = vi + at
There,
v is the final velocity, vi represents the initial velocity, a represents the acceleration and t represents the time.
The second equation of motion:
The second equation of motion in which the velocity relationship with the equation is shown is written there.
s = xit + 12 at2
There, s represented the displacement of the moving object, xi represented the initial velocity, a represented the acceleration and t represented the time.
Third equation of motion:
The third equation of motion can be used to analyze the objects that can fall from the height or can also be used to analyze those objects or bodies that can be moved on the highway with high velocity or speed.
v2 = xi2 + 2as
There, v represented the velocity, xi represented the initial velocity, a represented the acceleration of the moving object and s represented the displacement.
Vector nature of velocity:
Somehow the velocity and the speed are the same but their nature is different because speed is the scalar quantity and the velocity is the vector quantity because it can provide both magnitude and direction. the direction of the velocity is along with the displacement and their direction shows the final point or destination of the displaced object while the magnitude of the velocity is always their speed. Due to the vector nature of the velocity we can use different vector algebraic methods to add or subtract the multiples or the complex velocities efficiently. Numerous objects have different velocities that can act on the body at the same time so understanding them is crucial to understanding the fundamental concept of velocity.
Difference between speed and velocity:
The major differences between the speed and the velocity are given there:
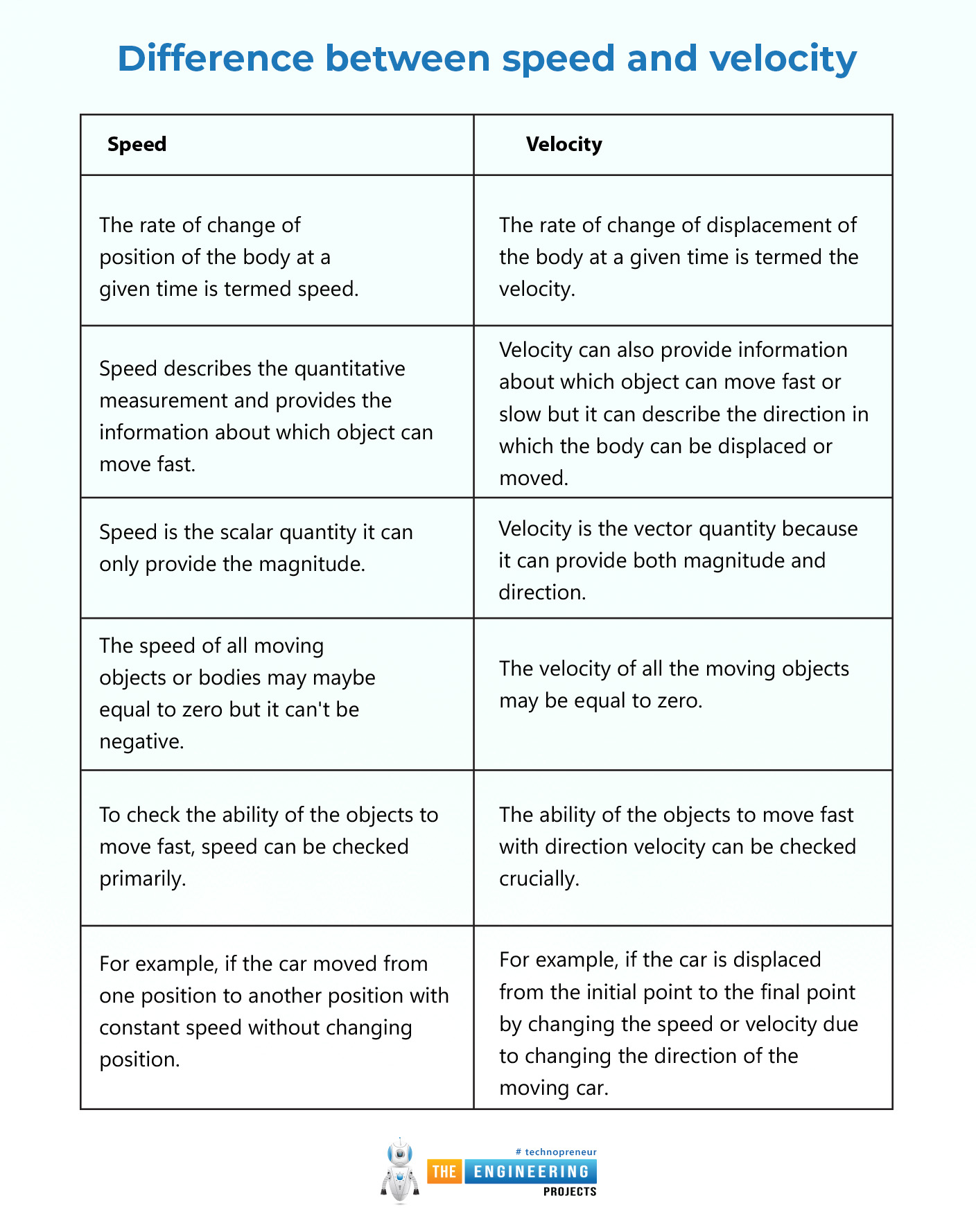
Speed |
Velocity |
|
|
|
|
|
|
|
|
|
|
|
|
Calculation of velocity:
Velocity can be calculated easily but its calculation depends upon the dimension in which the velocity occurs. It can also depend upon the cartesian coordinate system which can be used to represent the velocity. if the velocity can lie on one dimension then it can be calculated easily by dividing the total displacement by the total time taken which can be used by the object to change its position. but if the velocity can lie on the cartesian plane with two or three dimensions then to solve their complexity we can use different vector rules for their division. Some calculations of velocity according to dimension with examples are given there:
Velocity in one dimension:
When the body can be moved in one dimension then the value of velocity may be positive or negative because the negative and positive velocity describe the direction of the moving body in a single dimension on the x-axis. When the velocity can occur in one dimension then for their calculation we can use the given formula:
v =x2- x1t
There, v represented the velocity and x1 , x2 represented the change of the body from the initial point to the final point and t represented the time taken that can be used to change the position. As we know,
△d = x2 – x1
So the formula can slo be written as,
v = Δdt
As we know Δd represents the displacement of an object.
Velocity in two dimensions:
The complex velocity can occur in more than one dimension like in a dynamic field when two or more objects can be moved then it is complex so we can use the vector rules and it can also help to understand the motion of the body crucially. If the body can be moved in two dimensions, it starts its velocity from the point ( x1, y1 ) to the endpoint ( x2, y2 ) in some time. Then to calculate the velocities we can use the given formula which can be written below:
v = (x2- x1) i + (y2 - y1) jt
There, i, j are the unit vectors of the x and y directions in the cartesian coordinate system.
Velocity in three dimensions:
The complex velocity can occur in more than one dimension like in a dynamic field when two or more objects can be moved then it is complex so we can use the vector rules and it can also help to understand the motion of the body crucially. If the body can be moved in three dimensions, then it starts its velocity from the point ( x1, y1, z1 ) to the endpoint ( x2, y2, z2 ) in some time. Then to calculate the velocities we can use the given formula which can be written below:
v = (x2- x1) i + (y2 - y1) j + ( z2- z1) kt
There,i, j and k are the unit vectors of the x and y directions in the cartesian coordinate system.
Examples:
Example of velocity in one dimension:
Suppose the body or an object can be moved from the initial point with the speed of 3m and reach the end with the speed of 7m in 5s. Then find the velocity when the body is displaced in the right or positive direction.
To find:
v =?
Given:
x1 = 3m
x2 = 7m
t = 5s
Formula:
v =x2- x1t
Solution:
By using the above formula
v =x2- x1t
By putting the values
v = 7 - 35
v = 45
v = +0.8 ms-1
But if it can move to reverse and move negative direction then,
x1 = 7m
x2 = 3m
t = 5s
By using the formula
v =x2- x1t
By putting the values
v = 3 - 75
v = -45
v = – 0.8 ms-1
Example of velocity in two dimensions:
suppose the body or an object can be moved from the initial point with the speed of (3m, 4m) and reach the end with the speed of (7m, 8m) in 4s. Then find the velocity, magnitude, and direction.
To find:
v =?
v = ?
θ = ?
Given:
x1, y1 = 3m, 4m
x2, y2 = 7m, 8m
t = 4s
Formula:
v = (x2- x1) i + (y2 - y1) jt
Solution:
By using the above formula
v = (x2- x1) i + (y2 - y1) jt
Now by putting the values
v = (7- 3) i + (8 - 4) j4
v = 5+44 , v = 1.25 i + 1j ms-1
Magnitude:
Now apply the formula of magnitude
v = (A)2+ (B)2
Putting the values in the formula
v = (1.25)2+ (1)2
v = 1.7 + 1
v = 1.6 ms-1
Direction:
To find the direction we can use the given below formula:
θ = tan-1(BA)
Now by putting the values
θ = tan-1(11.25)
example of velocity in three dimensions:
suppose the body or an object can be moved from the initial point with the speed of (3m, 4m, 6m) and reach the end with the speed of (7m, 8m, 10m) in 4s. Then find the velocity and magnitude.
To find:
v =?
v = ?
Given:
x1, y1, z1 = 3m, 4m, 6m
x2, y2, z2 = 7m, 8m, 10m
t = 4s
Formula:
v = (x2- x1) i + (y2 - y1) j +( z2- z1) k t
Solution:
By using the above formula
v = (x2- x1) i + (y2 - y1) j +( z2- z1) k t
Now by putting the values
v = (7- 3) i + (8 - 4) j + (10-6) k4
v = 5+44 , v = 1.25 i + 1j + 4k ms-1
Magnitude:
Now apply the formula of magnitude
v = (A)2+ (B)2 +(C)2
Putting the values in the formula
v = (1.25)2+ (1)2+ (4)2
v = 1.7 + 1+ 16
v = 4.32 ms-1
Graphical representation of the velocity:
Velocity is the vector quantity or sometimes it becomes more complex so it can be represented in graphic form. The graphic representation of velocity is given there:
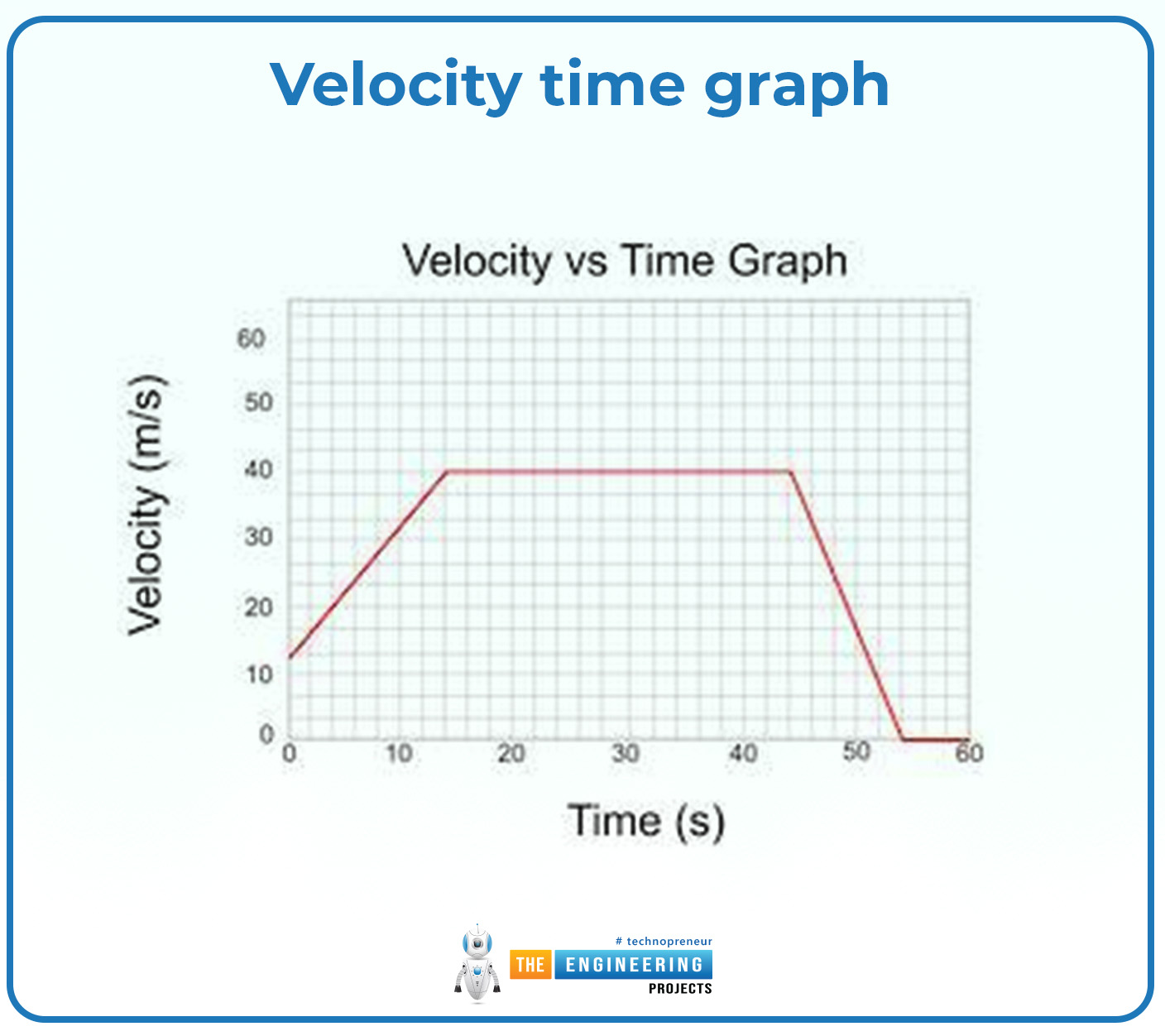
Velocity time graph
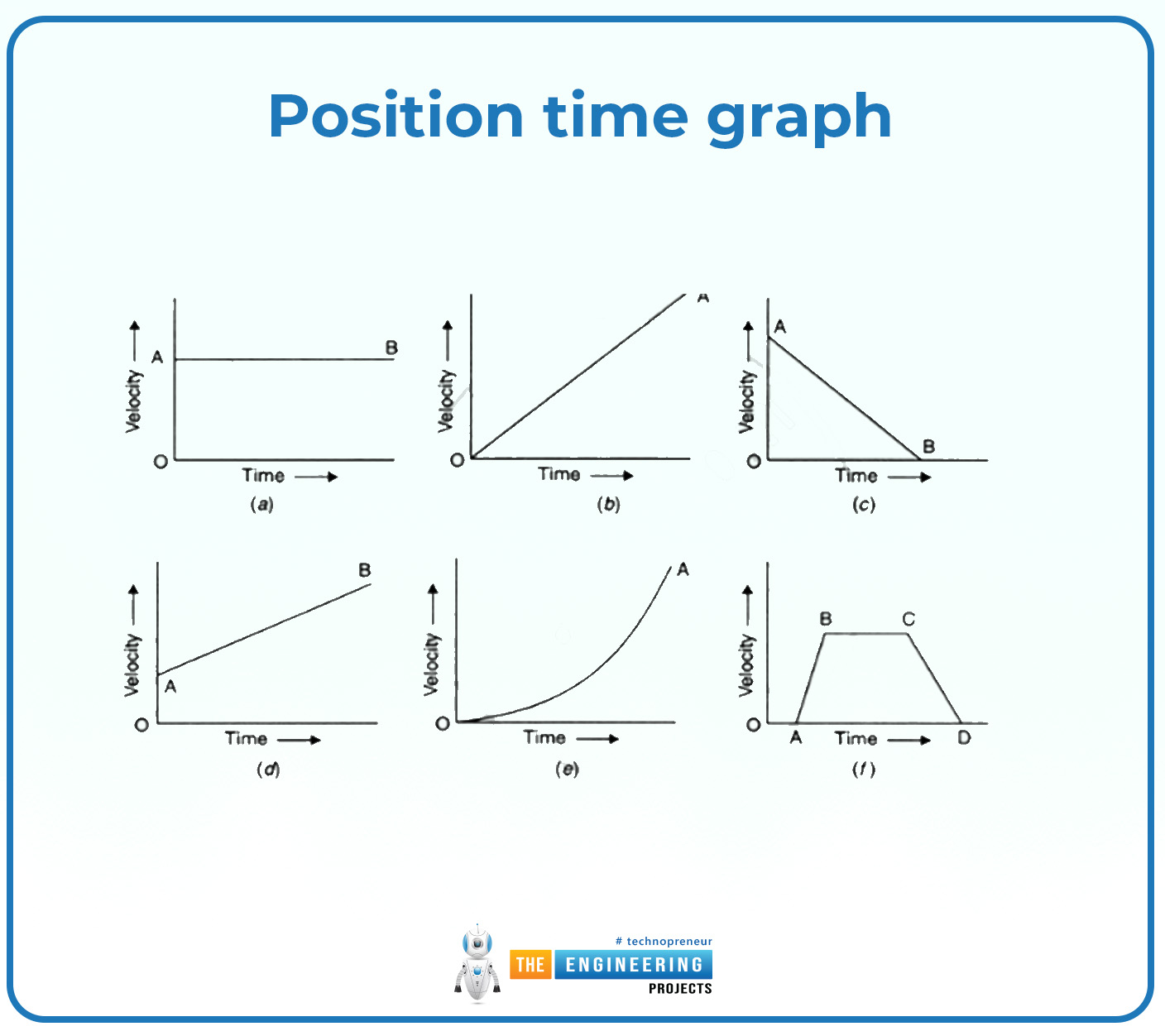
Position time graph
Velocity time graph:
In the velocity time graph, the whole area which is under the graph represents the displacement that can be covered by the moving object or body or the slope in the velocity time graph represents the acceleration of the moving object.
Position time graph:
In the position-time graph of the velocity the straight curve represents that the velocities are constant, curved slope represents that the velocities are not constant but if the slope suddenly becomes curved then it indicates that the velocities are instantaneous. and all of these velocities with their graph are drawn below.
Some applications of velocity in different fields:
Velocity can play a very fundamental role in different fields like physics, dynamics, and many others some of their applications are given there:
Medicine: in the field of medical sciences, the concept of velocity is used to understand the blood flow or the movement of body parts.
Navigation: velocity helps the pilots and sailors control the speed of the boat and ship.
Engineering: design the new machines after analyzing the velocity.
Sports: velocity helps athlete increase their performance in swimming, running, or other sports activities.
different coordinate systems:
Mostly the complex problems of velocity can be solved by using the given system because they are vectors and vectors are complex and solved by the algebraic methods in some coordinate systems. the higher dimensions problems can be solved in the given coordinate systems.
Cartesian coordinate system
Spherical coordinate system
Polar coordinate system.
Conclusion:
In the field of physics, concept of the velocity is crucial to understand because it helps to understand the motion of a moving object efficiently. Velocity can provide the quantity measurement of the moving object, due to its vector nature it can provide both magnitude and direction also.in dynamics or kinematics, velocity helps to understand the behavior of the moving body or object because it can play a very fundamental role in the motion of all bodies or objects. After reading this article the reader can find or understand the velocities that can occur in one direction or dimension or may occur in more than two or three dimensions.



