
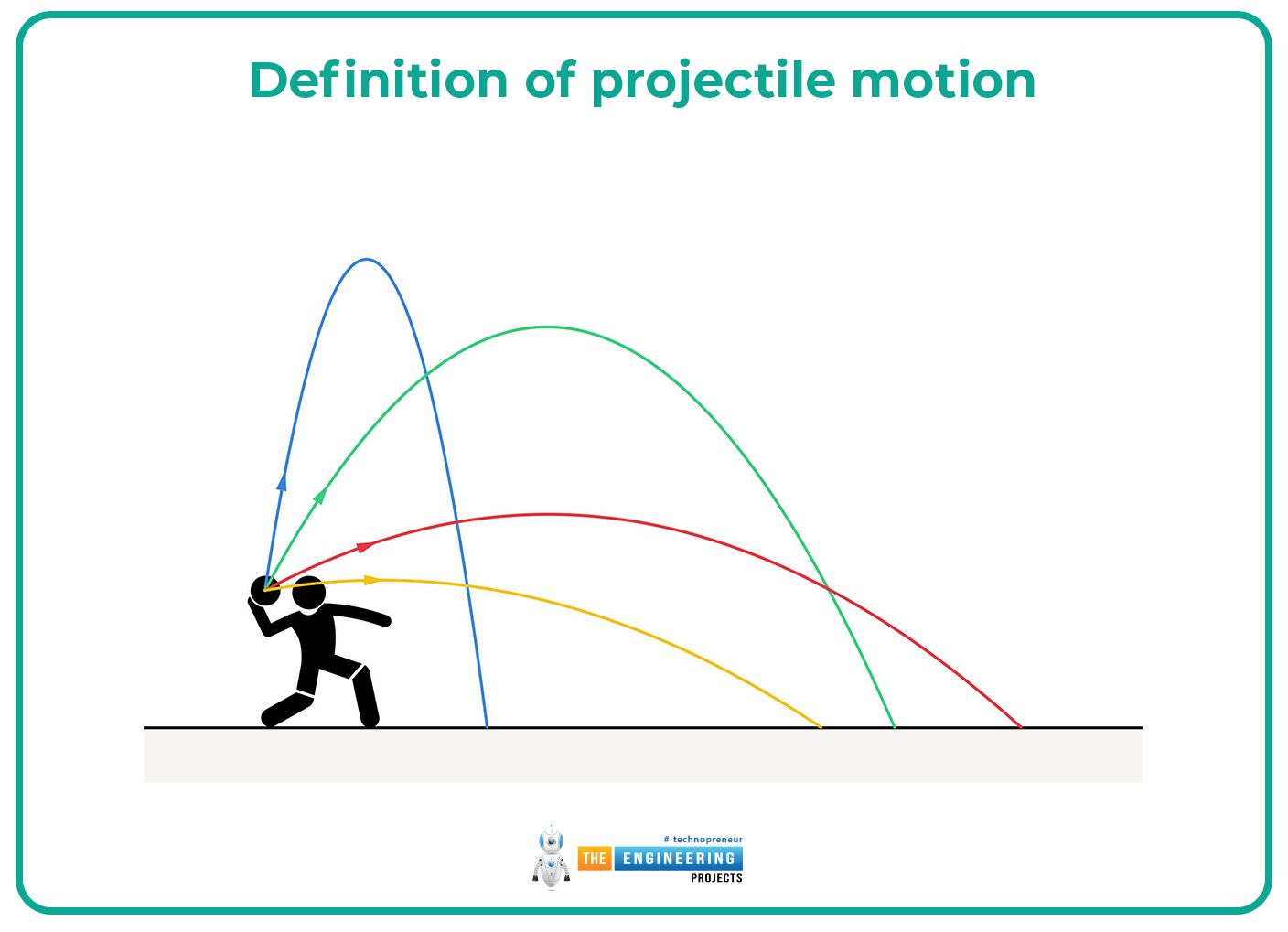
Hello friends, I hope you are all well and doing your best in your fields. In this post, we can explore the fundamental concept in physics: projectile motion. Projectile motion is the motion of the moving particle or the moving body that can be projected or motion near the earth's surface. Still, the particle can be moved according to the curve path or under the force of gravity and the gravity line. In history first, galileo represented particle motion in the form of projectile motion which can occur in the form of the parabola( the u-shaped curved or mirror-symmetrical in which the particle can be moved) or the motion of the particle which may occur in a straight path in the like if the ball throw downward from upward their motion path is straight.
The detailed or fundamental concept of projectile motion is essential to understand in different fields like mechanics, astronomy, or military sciences because it can help to understand the motion of rockets that can be used in wars. If the rocket can be launched from the earth to the next point it can do the projectile motion because they can be moved on the parabola. Now in this article, we can discuss and explore the projectile motion, its introduction, definition, mathematical representation, applications, numerous problems, and their significance.

What is Projectile Motion?
Projectile motion can be defined as:
“The two-dimensional motion of the moving particle or the object with their inertia, and under the constant acceleration or the gravitational force is termed as projectile motion.
Examples:
Some examples of trajectory motion are given there:
When the footballer player kicks the ball from one point then the ball follows the parabola and reaches the other this is the trajectory motion.
The bullet can be fired from the gun.
The ball can be thrown from an upward to a downward direction
The rocket or the missile can be launched and moved toward space under constant acceleration or the force of gravity.
What is Projectile Trajectory?
The trajectory is defined as:
“The path which can be followed by the projectile motion particle or object is termed the trajectory. The path that can followed by the projectile particle are parabola so their trajectory is the parabola.”
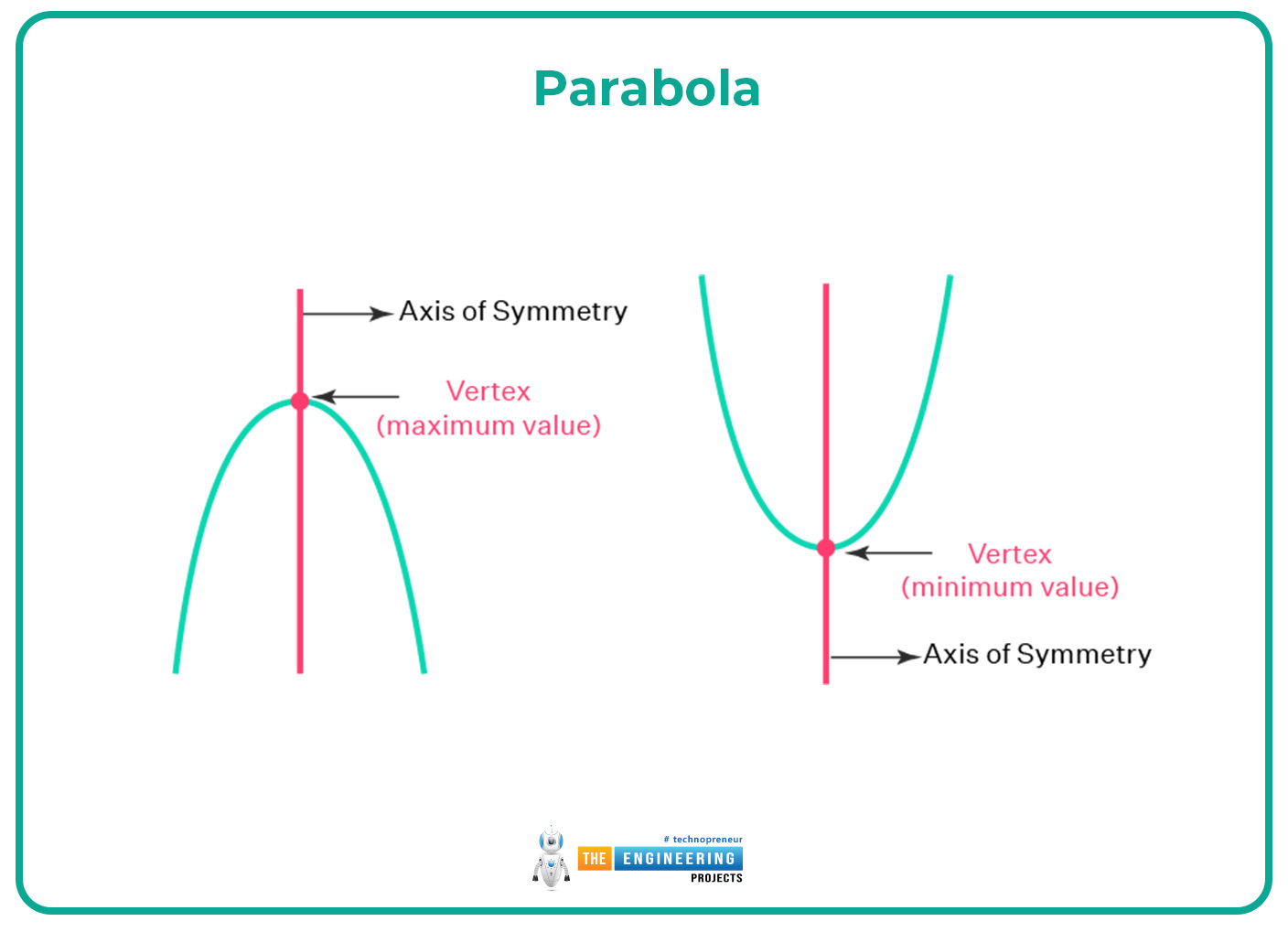
Parabola:
The parabola is the curve in which the projectile motion occurs and their curve is mirror-symmetrical or may be like the u- shaped. In parabola two dimensional motion can occur and it can occur in the dimension of x and y.
Equations for parabola:
The equation or formula of the parabola is written below:
In the dimension of the x-axis:
y = a ( x -h)2 + k
There,
a represents the constant acceleration, and h represents the height but in this equation, both h and k are the vertexes of the parabola.
In the dimension of the y-axis:
y = a ( y -k)2 + h
There,
a represents the constant acceleration, and h represents the height but in this equation, both h and k are the vertexes of the parabola.
Ballistic:
Ballistic is defined as:
“The study of the projectile motion is termed as the ballistic and the study of the projectile motion trajectory are termed as the ballistic trajectory.”
Explanation of the projectile motion:
The fundamental explanation of the projectile motion with their basic principles ( horizontal motion, vertical motion ) is given there:
The motion of an object in a horizontal direction:
When the body or the ball can be thrown from upward with the angle or the initial velocity then it can be moved forward because of the moving body inertia and falls downward because of the constant gravitational force acting on it. So according to this, in the horizontal direction of motion, no forces acted on it (only gravitational force act on it) so that is why the acceleration in the horizontal direction is equal to zero as,
ax = 0
The motion of an object in a vertical direction:
When the body or the ball can be thrown from upward with the angle or the initial velocity then it can be moved forward because of the moving body inertia and falls downward because of the constant gravitational force acting on it. According to this, in the vertical direction of motion, forces acted on it so that is why the acceleration in the horizontal direction is equal to g, and g = 9.8ms2 .
Derivation:
The path of the trajectory can be determined through the given equation, their derivations are written below:
As we know the second equation of motion,
S = vit + 12at2
There,
vi represent the initial velocity, a indicates the acceleration and t represents the time.
X dimension:
In the x dimension, we can write this formula as:
x = vixt + 12at2
As we know, in the x dimension the acceleration is equal to zero so,
ax = 0
x = vixt + 12(0)t2
So,
x = vixt + 0
x = vixt
Y dimension:
In the y dimension, we can write this formula as:
y = viyt + 12at2
As we know, in the y dimension the acceleration is equal to g so,
ax = -g
y = viyt + 12(-g)t2
So,
y = viyt - 12gt2
Special case:
In some special cases when the projection of the moving body is projected horizontally from some certain height then,
y = viyt - 12gt2
Then,
viy = 0
y = (0)t - 12gt2
y = 12gt2
Instantaneous velocity:
Consider the projected body that has the initial velocity vi and at the horizontal direction the angle θ can be formed between them so the initial velocity for horizontal or vertical components is equal to cos or sin, their equation is written below:
Initial velocity for the horizontal component = vix= vi cosθ
Initial velocity for the vertical component = viy = vi cosθ
Their detailed derivation is given there:
Velocity for the horizontal component:
On the horizontal dimension moving object, no force acts on it only gravitational force acts on it so that's why the acceleration is equal to zero and written as:
ax = 0
As we know the first equation of motion
vf= vi + at
So the velocity for the horizontal component in the x dimension is written as:
vfx= vix + axt
ax = 0
So,
vfx= vix + (0)t
vfx= vix + (0)
vfx= vix or it also equal to,
vfx= vix = vi cosθ
Velocity for the vertical component:
On the vertical dimension of moving objects, the forces acting on it or the acceleration are equal to g,
ay = -g
As we know the first equation of motion
vf= vi + at
So the velocity for the vertical component in the y dimension is written as:
vfy= viy + ayt
ay = -g
So,
vfx= viy + (-g)t
Or,
viy = vi cosθ
So,
vfx= vi cosθ - gt
Magnitude of the velocity components:
The magnitude can be determined for the components that can be moved in two dimensions. The formulas which are used for determination are given there:
v= vfx2 + vfy2
There,
v represented the velocity of the components, vfx represented the final velocity for the x components, and vfy represented the final velocity for the y components.
Direction of the velocity components:
In the two-dimensional components, the resultant velocity can form the angle θ between their horizontal components the formula for determining their direction is given there:
tan Φ = vfyvfx
Or,
Φ = tan-1 vfyvfx
Displacement of the velocity:
The displacement can covered by the projectile object in the time t so the displacement in the horizontal or the vertical component can be written as:
x = vixt cos θ
y = viyt sinθ - 12gt2
So, to find the magnitude of the two dimension body displacement we can use the given formula:
Δ r = x2 + y2
Now let the both equations as:
x = vixt cos θ, y = viyt sinθ - 12gt2
Then, eliminate the time from the above equation and write them as,
y = tan θ. x - g2v2 cos2θ . x2
So, we know that
R = g2v2 cos2θ
R indicates the range of the projectile motion
So,
y = tan θ. X - x2R
The g, angle is x2so it can also be written as,
y = ax + bx2
This equation or the formula can slo be used for parabola but the angle can be formed and this equation can be written as,
v = x2gx sin2θ - 2y cos2θ
Displacement of the components in the polar coordinate system:
Displacement of the components can also be shown in the polar coordinate system or in the cartesian coordinate system. For the determination of the displacement in the polar coordinate system, we can use the given formula which is written below:
r ф = 2 v2 cos2θg (tan θ secф - tan ф secф )
According to the above equation or derivation, we know that,
y = r sinθ
or , x = r cosθ
Properties of the projectile motion:
There are some basic properties of the projectile motion or the trajectory which are given there:
Maximum height of the projectile:
The maximum height of the projectile object is when the projectile object can reach the highest point or the projectile object covered the maximum distance to reach the peak is termed as the maximum height of the projectile object.
To determine the maximum height of the projectile motion we can use them,
The initial velocity for the projection of the object = viy= initial velocity in the vertical component = viy = vi sinθ
So we can also know that the acceleration in the vertical velocity the acceleration is equal to g
ay = -g
Or the final velocity when the projectile object can be reached at the maximum height,
vfy = 0
So,
= v sinθ - gth
So the time that can used to reach the maximum height,
th= 2v sinθg
There, th indicates the time of the projectile motion to reach the maximum height.
As we know,
2aS = vf2 - vi2
Or this equation can be written as,
2ayy = vfy2- vfx2
This equation is used for the vertical component
Now put the values in this equation and write them as
2(-g) H = (0) - ( visinθ)2
Then,
-2gH = vi2 sin θ2
Then, the height of the projectile motion can be determined by,
H = vi2 sin θ22g
There, H indicates the height of the projectile motion of the moving objects.
When the maximum height is reached then the sin θ = 90°
Hmax = vi2 ( 0)2g
Hmax = vi2 2g
So the maximum height when the angle formed between the vertical and the horizontal components we can use the given formula:
H = (x tanθ)24 ( xtan θ -y)
Now to find the angle of the elevation at the maximum height we can determine this by using the given formula which is written below:
Φ = arctan tan θ2
Range of the projectile:
the maximum distance that can be covered by the projectile body in the horizontal direction is termed the range of the projectile.
To determine the range of the projectile in the horizontal direction we can use the given formula that can be derived from different equations so the derivations are given there:
As we know,
x = vix t + 12 axt2
So,
vix = vi cosθ
t = 2v sinθg
ax = 0
x = R
So, according to this,x = vix t + 12 axt2, this equation can be written as,
R = vi cosθ 2vi sinθg + 12 (0)t2
R = vi cosθ 2vi sinθg + 0
R = vi2 ( 2sinθ cosθ)g
We also know that 2sinθ cosθ = sin 2θ
R = vi2 sin 2θg
Relationship between the maximum height and the horizontal range:
The relationship between the maximum height and the horizontal range can be proved through the given derivation and formula which are given there:
As we know,
H = vi2 sin θ22g
We can also know that,
d = vi2 sin2 θ2g
Then we can compare both of these equations to prove the relationship between them,
hd = vi2 sin2θ2g gvi2 sin2 θ
hd = sin2θ4 sinθ cosθ
So,
H = d tan θ4
Then, the height of the projectile can equal the range of the projectile of the body
H = R
Time of the flight of the projectile:
The time of flight of the projectile body can be defined as the time that can be used to cover the distance from their launching to reach the end where the projectile body can be taken off. Simply the time that can be used for the moving projectile body to hit the ground is termed as the time of flight of the projectile body.
When the projectile body starts initial velocity can go up but again come back to the ground with the same velocity so it cant cover the vertical distance we know that the vertical distance is equal to zero and written as:
y = 0
So we know that,
The initial velocity which is used by the projectile body = viy = vi sin θ
The acceleration in the vertical velocity which is due to the force of gravity ay = -g
Then we can determine the time of the flight by using the equation which is given there:
S = vit + 12 at2
Then put these values or rewrite the equation as;
y = viyt + 12 ayt2
Then,
0 = ( vi sinθ) t - 12 gt2
12 gt2 = ( vi sinθ) t
t = 2vi sinθ g
According to the given equation, we can eliminate the air resistance but if the time of the projectile body vertical direction with the height at 0 then it can be written as:
t = dv cos θ
There, d represented the displacement. So it can be written as:
t = v sinθ + ( v sin θ2) + 2gyg
Now solve this equation as
t = v sinθ + ( v sin θ2) + 0g
t = v sinθ + ( v sin θ2) g
Then eliminate the by the 2 power and write them as
t = v sinθ + v sin θg
t = 2v sinθ g
If the θ = 45°
Then put this value in the equation
t = 2v sin(45)g
t = 2v sin22g
t = 2vg
Maximum range of the projectile:
The projectile body can reach the maximum range when the sin 2θ reaches the maximum value because sin 2θ = 1 there, to find the maximum range we can use the given formula and determine them. Their formula with derivation is written below:
As we know,
Sin 2θ = 1
2θ = sin-1 (1)
Or, sin-1 (1) = 90°
2θ = 90°
But, θ = 45°
We can also that,
R = vi2 sin 2θg
Then put the value of θ
R = vi2 sin 2(45)g
R = vi2 sin (90)g
sin 90° = 1
R = vi2 (1)g
R = vi2 g
The maximum range of the projectile motion can be written as the:
R = Rmax = sin 2θ
Ballistic:
Ballistic is defined as:
The study of the motion of the projectile body is termed as the ballistic.
Detailed exploration of the ballistic is given below:
Ballistic flight:
Ballistic flight can be defined as:
The projection of the body starts when an external force is applied or can ut the initial push then the object can be moved freely without any restriction or the object move with inertia or also due to the force of gravity that can act on the projectile body this types of flight are termed as the ballistic flight.
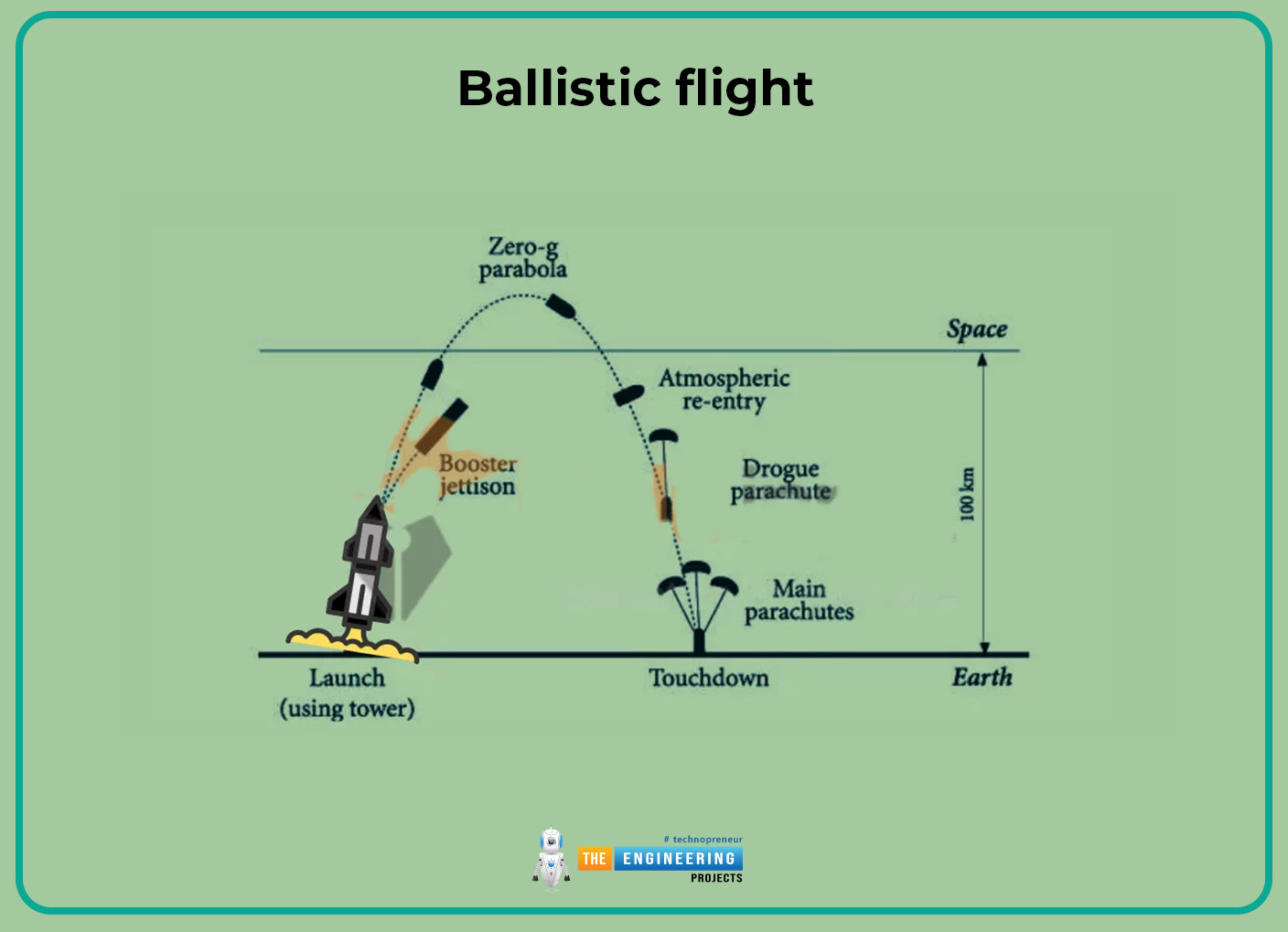
Ballistic missile;
Ballistic missiles are the type of ballistic flight in which the missile can do projection with un-powered or also with un-guided. Ballistic missiles are used in the wars by the military or also in astronomy.

Ballistic trajectory:
The path or the curve that can followed by the ballistic missile or the ballistic flight is termed as the ballistic trajectory.
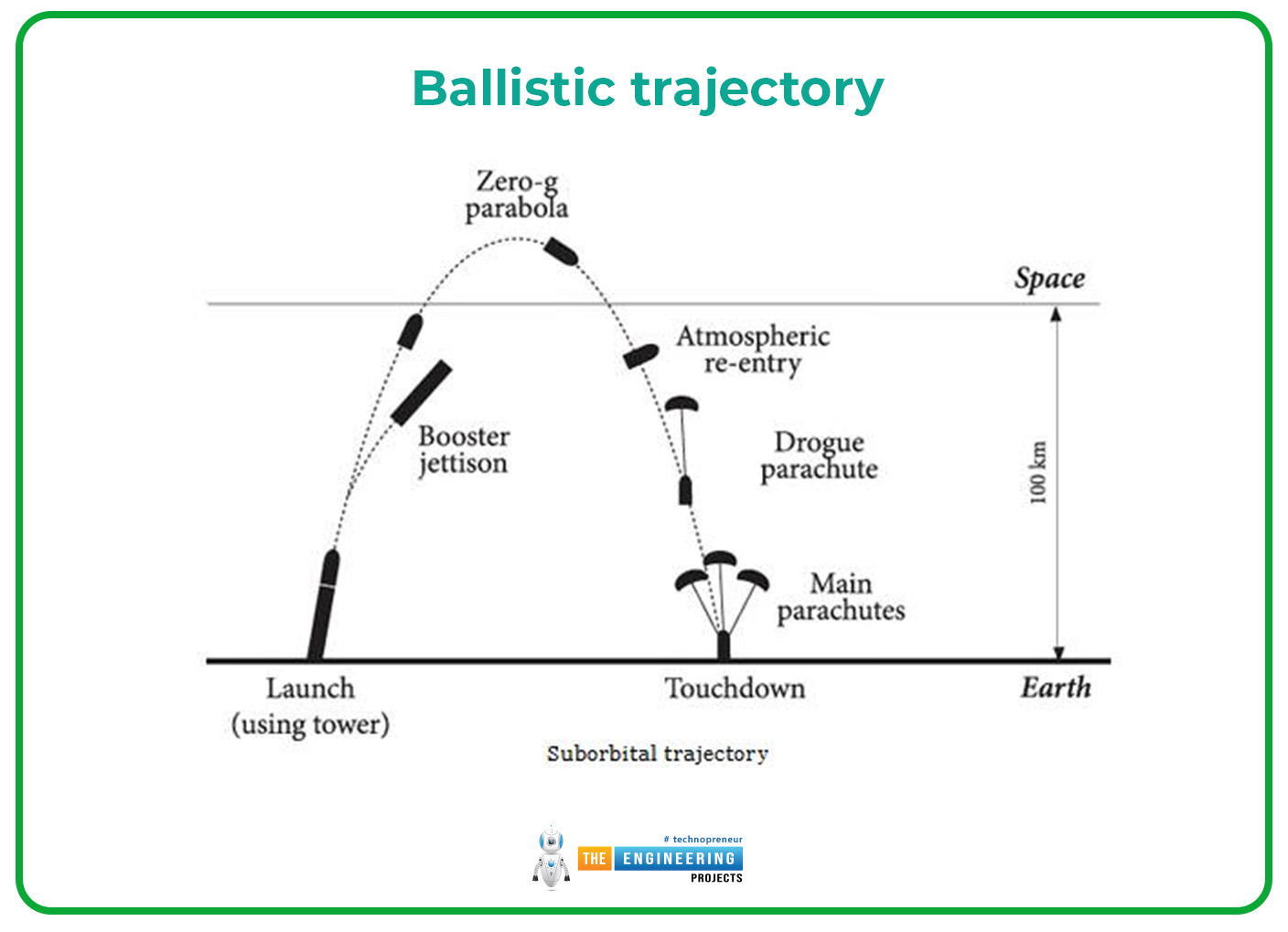
Description:
A ballistic missile can follow the ballistic trajectory but the missile or the flight can be moved due to the two independent motions through which the body can be moved freely and reach its destination. The two main or independent positions are given there:
The force of gravity and the inertia of the body help the object to move or follow the parabolic path which can do the projectile motion or the ballistic flight. Both of these forces are essential for the free motion of the projected body and reached to their destination.
The projectile body can fly or in starting follow the strength path in the direction of launching and then follow the parabolic path or do the projectile trajectory.
In ballistic flight the effects of the inertia:
Interia is the force that can help the body to move straight with the force of gravity. But with the force of inertia, the projectile body can move straight or fall to the point where its destination is fixed or reach the point where it can be thrown down. However, due to the effect of inertia, the constant speed or the velocity is always equal to the initial speed or the velocity in space.
In ballistic flight the effects of the force of gravity:
When the body can be moved it can do a straight motion due to the effect of inertia but the trajectory path or the parabola path can be followed by the due to the force of gravity. Because the force of gravity turned the body or the object to move in teh curved space and helped to attract into the ground and reach its destination.
Short ranges or the flat surface or earth:
For the short-range motion or if the motion reaches the earth then the projectile body always follows the parabolic path due to the effect of inertia and the force of gravity.
Long ranges or the spherical earth:
The long-range motion of the projectile body or the projectile body that can be moved in the spherical earth is termed elliptical.
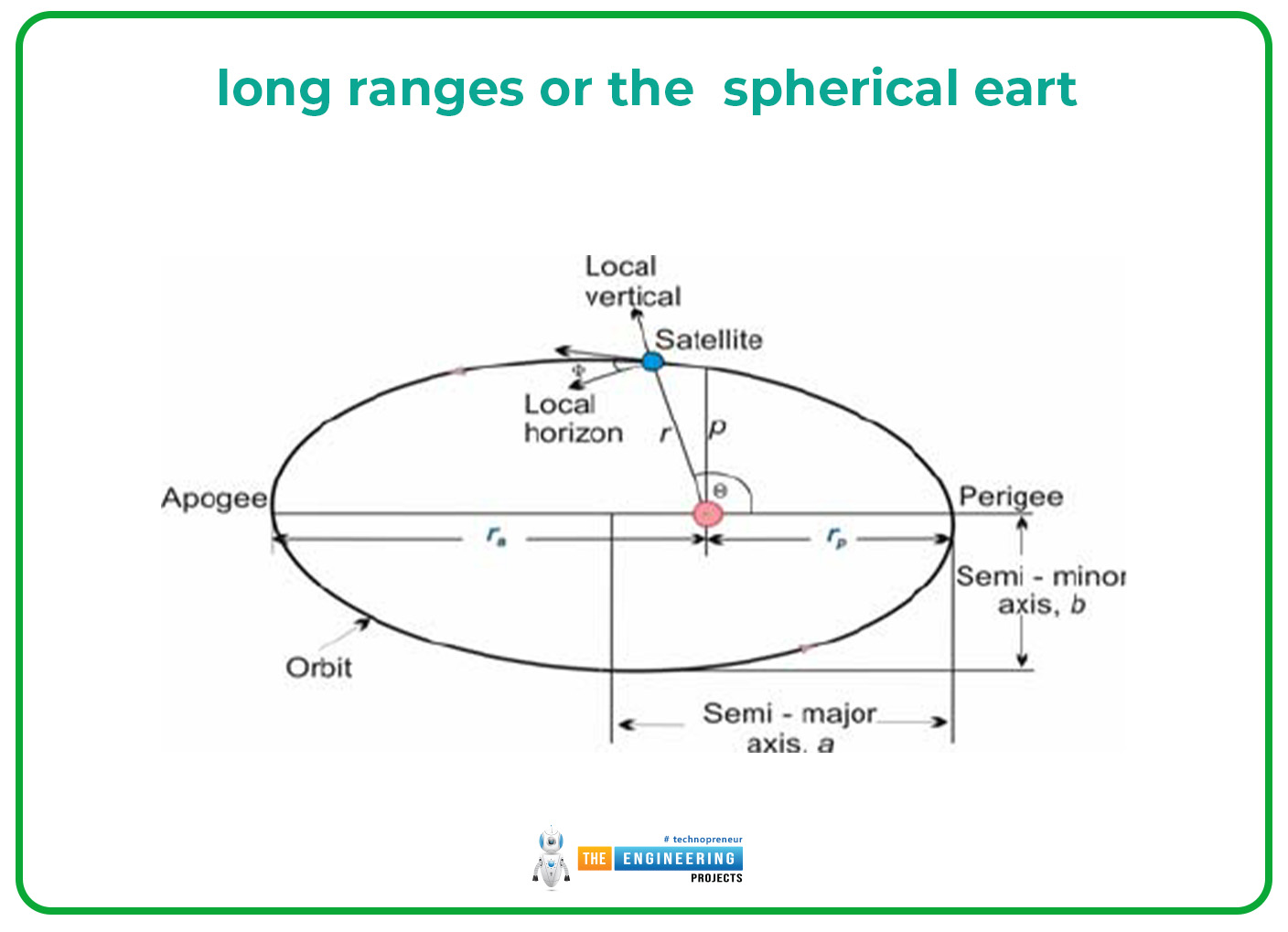
This trajectory path is mostly followed by missiles which are used in wars or also used when rockets or missiles are launched.
Major uses of ballistic missiles:
Some major uses of ballistic missiles are given there:
Short ranges: ballistic missiles or ballistic trajectors are mostly used for short ranges they are not used mostly for long ranges.
Long ranges: for the long ranges ballistic missiles or ballistic trajectories are used but these can used by controlling them from remote and also launching these missiles by providing complete guidance to them.
Air friction: when the trajectories are moved with a high velocity then the air resistance can't be neglected it can calculated with the air friction. Because mostly the air friction in the atmosphere or space is greater than the force of gravity that’s why it can't be neglectable.
Aerodynamic forces: when teh force of gravity becomes less according to the air resistance and it affects both horizontal or vertical component motion so then we can't neglect the aerodynamic forces which are mostly air resistance.
Effect of the aerodynamic forces:
Aerodynamic forces can affect the projection directly because the air resistance can create many different problems in the flight so for the projectile motion, the moving projectile body needs a high level of the projection angle to move efficiently.
Factors affecting the projectile motion:
The factors that affect the motion of the projectile bodies are given there:
Air resistance
Initial velocity
Height of launch
Angle of projection
Air resistance:
Now in the calculation of the projection of the projectile bodies, air resistance can't be neglected because air resistance and other aerodynamic forces can affect the projectile bodies' projection, height, and ranges.
Initial velocity: ( vi)
The initial velocity can directly affect the projectile motion because if the initial velocity is high then the projection and the height of the flight are also high and reach their destination with the high velocity and speed.
Height of launch:
When the projectile body moves or is launched at a high height then its range and the time that can be taken by it to be thrown are increased because its height or range with the angle of projection are increased.
The angle of projection: (θ)
The angle of projection directly affects the range and the height of the projectile body because if the angle is increased then they have a high projection, the optimal angle of projection is 45 if we neglect the air resistance then at this angle, the body can be reached at its maximum height.
Applications of the projectile motion:
Some major applications of the projectile motion are given below:
Space exploration: understanding and analyzing the projectile motion can help in space exploration to study the stars and galaxies.
Engineering: understanding and analyzing the projectile motion can help in engineering to manufacture the rockets and missiles which are used in teh wars or used in space exploration.
Sports: projectile motion also helps in sports like when we use a gun then the projectile motion concept is essential to understanding teh process of fire.
Military: in the military projectile motion is fundamental because the rockets and the missiles being used move according to the trajectory path which is understood after clearing the concept of projectile motion.
Applications of the projectile motion:
Some applications of the projectile motion in the advanced topics are given there:
The motion of the projectile body in non-uniform gravitational fields.
Air resistance
Drag force
Spin and Magnus effect
Study of projectile motion experimentally:
To study the projectile motion or the projectile trajectory through experiment the engineers can use different types of machines or instruments like motion sensors, tracking software, or different types of high-speed magnification cameras and lenses to see or analyze the trajectory path of the projectile body and through analyze they can improve the theoretical model which re based on the projectile motion. Experimental studies of the projectile motion help to precise or accurate the different models and also help to understand their applications in different fields.
Conclusion:
In different fields of physics, mostly in mechanics or astronomy projectile motion is used to understand the motion of the projected objects and also help to understand the motion or the trajectory path because, in projectile motion, motion is affected by the force of gravity and inertia also. In the projectile motion, we can analyze the path, range, and maximum height of the projected objects precisely and accurately. After understanding these basic properties and the principle of the projectile motion we can use this in different fields like in engineering or mainly in the military. Now modern or advanced topics like air resistance or the different forces effects can be analyzed easily through understanding the projectile motion. After reading these articles the reader can understand the projection of the projectile motion efficiently.



