Hi friends, I hope you are all well. In this post, we can discuss the fundamental concept of collision crucially. Generally, collision is the interaction between two moving bodies because when two bodies interact then they can change their direction during the motion. In physics, we can deal with and understand the motion of the moving bodies so collision is a force that can exert the moving bodies when two or more bodies come in contact for a short period. In moving bodies when two bodies collide they can exert a high force and collide with each other with great force but in their collision, the kinetic energy always remains conserved.
When the collision occurs between the two objects, it can change their velocity because they can change their direction and move quickly. The change in the velocities after collision has a high difference and it can also be termed as the closing speed. kinetic energy is always conserved so that's why they also conserved the momentum. In atoms, the inside particles or all subatomic particles can also collide so to understand their collision it is compulsory to understand the types of collision and their significance. In the field of mechanics, kinematics the concept of collision is fundamental to understanding it. Now we can start our detailed discussion about the collision, its types, elastic collision, inelastic collision, special cases, examples, and their different natural phenomena.

What is Collision?
Collision is defined as:
“When the two particles collide with each other by exerting a high force, maybe their collision occurred accidentally but the forceful interaction between the two moving bodies or particles is termed as the collision.”
The collision can't be perfect because only in the ideal gases perfect collisions may be occurred but mostly perfect collisions aren't possible. The collision can mostly occur in gases or liquids or atoms because it can only occur when the free particles are present and do continuous or random motion their motion is not steady. Because in steady motion between two particles collision cant be occurred.
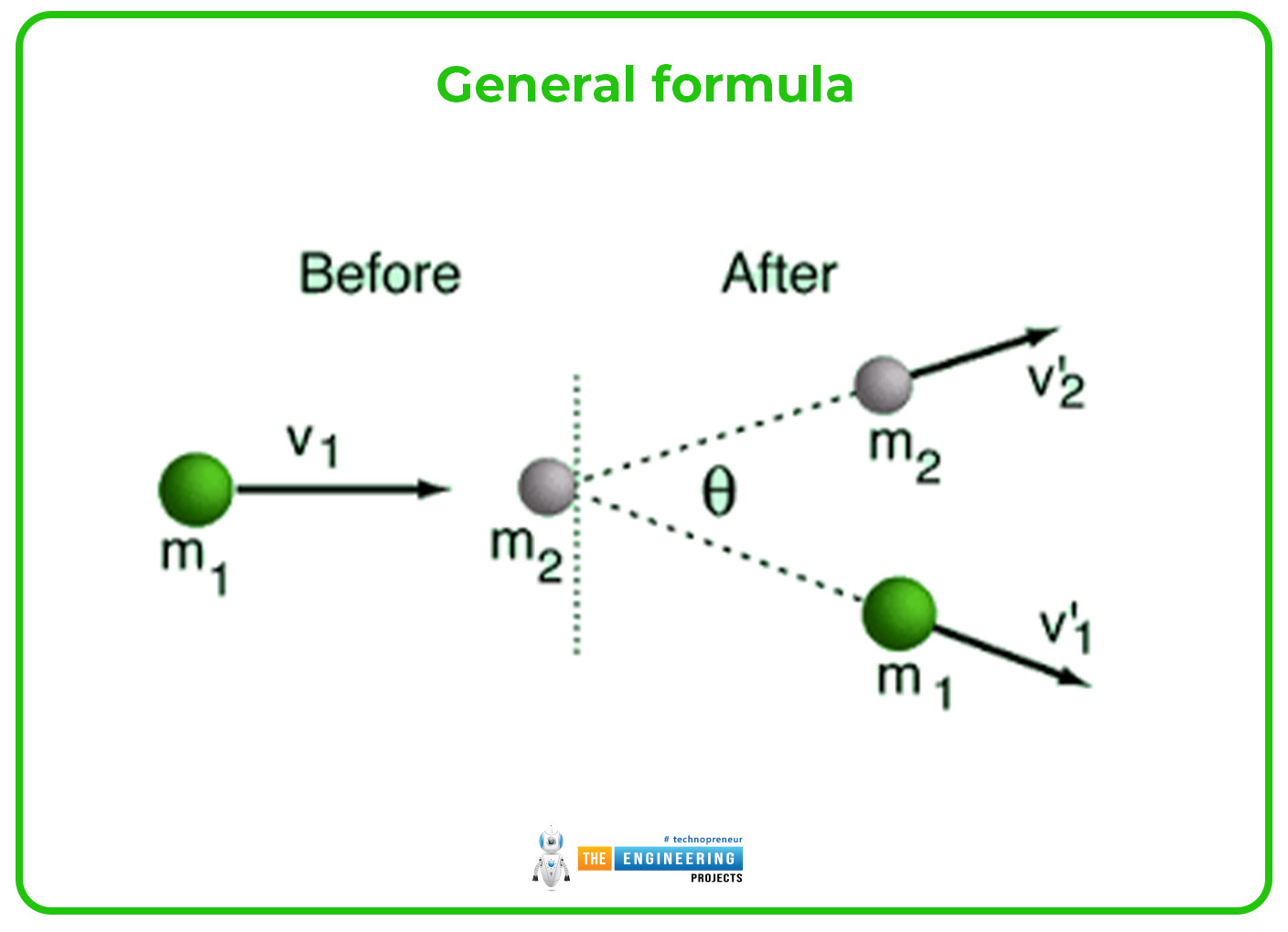
General formula:
The general formula that can be used for the collision between two bodies is written as:
m1v1 + m2v2 = m1v1' + m2v2'
There,
- m1 and v1 represented the mass and the velocity of the first moving object and m2 and v2 is the mass and velocity of the other object that can collide with the first object.
- m1 and v1' represented the mass and velocity of the first object after the collision and m2 and v2' indicates the velocity of the second object after the collision.

Collision Example:
When the ball bounces on a hard marble floor then it can also bounce back because it can collide with a hard surface momentum and the kinetic energy remains conserved but if the hard ball can bounce on a soft surface or the sandy surface then it can't bounce back and this collision of the ball with the sandy surface are inelastic collision because it can't bounce back and the elastic collisions are those in which the ball bounces back again.
When cricketers or football play a game on the field they can collide with each other with a great colliding force.
The car which can be moved on the road with high speed and velocity and suddenly collide with the other car then both collide with the high velocity or speed and exert the high colliding force.
Types of Collision:
Collison has common two types but they have three major types which can be written below with the detailed description and examples:
Perfect inelastic collision
Inelastic collision
Elastic collision
Elastic Collision:
Elastic collision is defined as:
“ when kinetic energy is conserved during the collision between the two moving particles or objects termed as elastic collision”
In this type of collision, always momentum and energy remain conserved. Elastic collisions are ideal because in this collision the kinetic energy of the colliding objects remains the same before the collision and after the collision. In surroundings rarely elastic collisions can be seen because they are ideal so that's why they can generally seen in between atoms or in between the subatomic particles or molecules.

In elastic collisions, the energy is conserved when no heat or sound energy can be produced. But the perfect elastic collision is not possible. when the two bodies collide with each other with great force firstly energy is converted from kinetic to potential then the particles again start moving then they again convert the potential energy into kinetic energy by creating the repulsive forces and by making the angle between their collision. Through this, the moving particles can conserve their energy. The elastic collision of the atoms can firstly shown by the rutherford through his atomic model. In the concept of elastic collision, the bodies that can collide with each other have the same mass so they can conserve both momentum and kinetic energy without releasing any energy in the form of heat, sound, or other. Elastic collisions only occur during the random or variable motion of the atoms or bodies like when the atoms of gases collide with each other then it can be shown the ideal elastic collision which is not possible.
Example:
When the hard ball hits the hard surface then it can bounce back with the same velocity because it can be shown the elastic collision in which the momentum and the kinetic energy are remained the same before and after the collision.
Law of conservation of momentum:
In elastic collision with the kinetic energy, the momentum can also be conserved so that is why it is important to understand the law of conservation of momentum. The simple statement in which the law of conservation can be defined is given there:
“The body that can be moved with linear motion, then the total momentum during their linear motion of the isolated system ( the system in which no external force can be exerted) can always remain constant.”
Mathematical representation:
Mathematical representations of the law of conservation of momentum are written below:
m1v1 + m2v2 = m1v1' + m2v2'
There,
m1 and v1 represented the mass and the velocity of the first moving object and m2 or v2 the mass and velocity of the other object that can collide with the first object.
m1 and v1' represented the mass and velocity of the first object after the collision and m2 and v2' indicate the velocity of the second object after the collision.
Elastic collision in one dimension:
To understand the elastic collision in one dimension let's suppose the moving bodies or the hard balls which are non-rotatable and have equal masses. Their masses can be represented through m1 or m2 and their velocities before collision are represented through v1 and v2, but when these two balls collide with each other their mass remains the same as the m1 or m2 but their velocity is changed, and represented as v1' or v2'.

Mathematical representation or derivation:
According to the above explanation, we know that m indicates the masses of the bodies and v indicates the velocities of the objects now it can be mathematically represented through the law of conservation of momentum and it can be written as:
As we know the law of conservation of momentum,
m1v1 + m2v2 = m1v1' + m2v2'
Then, when we arrange them and write them as,
m1v1 - m1v1' = m2v2' - m2v2
Or, when we take the m1 or m2 common then it can be written as:
m1( v1- v1' ) = m2 (v2'- v2) ………. (i) equation
We know that the elastic collision is the perfect elastic so in this collision, the kinetic energy is conserved totally and it can be written as:
12m1v12 + 12m2v22 = 12v1v1'2 + 12m2v2'2
Now arrange them according to their masses and write as
12m1v12 - 12v1v1'2 = 12m2v2'2 - 12m2v22
Now take the common m1, m2,
12m1 (v12 - v1'2 ) = 12m2 (v2'2 - v22)
Now cut the same value 12 on both sides and write as
m1 (v12 - v1'2 ) =m2 (v2'2 - v22) ……. (ii) equation
Now divide the equation (ii) from the equation (i) and write as
m1( v1- v1' ) = m2 (v2'- v2) ………. (i) equation
m1 (v12 - v1'2 ) =m2 (v2'2 - v22) ……. (ii) equation
Then,
m1 (v12 - v1'2 ) m1( v1- v1' ) = m2 (v2'2 - v22)m2 (v2'- v2)
As we know,
( v12 - v1'2 ) = ( v1 - v1' ) ( v1+ v1')
(v22- v2'2) = ( v2 - v2' ) ( v2+ v2')
Then we can put these equations in the above equations cut the same masses and write them as,
( v12 - v1'2 ) ( v1- v1' ) = (v2'2 - v22) (v2'- v2)
( v1 - v1' ) ( v1+ v1') ( v1- v1' ) = ( v2 - v2' ) ( v2+ v2') (v2'- v2)
Then,
v1 + v1' = v2 + v2'
Then arrange their velocities before and after the collision and write them as,
v1 - v2 = (v2' - v1')
Arrange them and write them as
v1 - v2= - (v1' - v2')
Now the given equation which is used for the elastic collision in one dimension shows that ( v1 - v2) shows the magnitude of the relative velocity of the 1st ball as compared to the second ball before the collision.
And v1' - v2' shows the magnitude of the relative velocity of the 1st ball as compared to the second ball after the collision.
And this represented that,
Speed of the ball approach = speed of the ball's separation.
Velocity in one dimension according to Newton:
For the final velocity of the moving particle according to the newton we can use the given formula:
v = ( 1+ e) vcom - ev
Or, v = vcom = m1 v1 + m2 v2m1 + m2
There,
vcom represented the two particles' center of mass related to velocity.
e represented the coefficient of the velocity restitution.
v is the initial and the final velocity which can be different before the collision or after the collision.
Relativistic of velocity in one dimension:
The formula of the special relativity that can be used in the relativistic velocity in one dimension, using the relativity formula is written below:
ρ = mv1 - v2c2
There,
ρ represented the momentum, m indicates the mass of the moving particle v represents the velocity and c indicates the speed of light. but according to this formula, the total momentum of the moving particles is equal to zero. And their description is written.
ρ1= -ρ2
So that is why, ρ12 = ρ22
And the E is equal to,
E = m12c4 + p12c2 + m22c4 + p22c2
Then,
v1 = -v1
After collision determination of velocities:
After the collision, the velocity can be calculated by using the equations of the moving objects or the particles. the details and formulas that can be used for the determination are given there:
Determination of the velocity v1' of the mass m1:
We can determine the velocity of the mass after collision by using the formula derivation and formula are given there:
As we know,
v1 - v2 = v2' - v1'
Then,
v2' = v1 - v2 + v1' ….. (i) equation
We also know that
m1( v1- v1' ) = m2 (v2'- v2)..... (ii) equation
Now put the equation (i) into the equation (ii)
m1( v1- v1' ) = m2 (v1 - v2 + v1'- v2)
m1v1 - m1v1' = m2v1 - m2 v2 + m2v1' - m2v2
Then arrange them,
m1v1' + m2v1' = m1v1 - m2v1 + m2v2 + m2 v2
Then,
v1' ( m1 + m2) = v1( m1- m2) + 2 m2 v2
Or,
v1' = v1 ( m1- m2)( m1 + m2) + 2m2(m1 + m2)v2 ……. (iii) equation
The above formula can be used to find the velocity of the mass after the collision.
Determination of the velocity v2' of the mass m2:
To find the velocity of the second mass after the collision we can use some equations their derivation is written below.
Now use the equation (i) and equation (iii)
v2' = v1 - v2 + v1' ….. (i) equation
v1' = v1 ( m1- m2)( m1 + m2) + 2m2(m1 + m2)v2 ……. (iii) equation
Now put the equation (iii) into the equation (i)
v2' = v1 - v2 + v1 ( m1- m2)( m1 + m2) + 2m2(m1 + m2)v2
v2' = v1 1 +( m1- m2)( m1 + m2) + 1-2m2(m1 + m2) v2
v2' = v1 ( m1- m2) + (m1+ m2)( m1 + m2) +v2 2m2 - (m1 + m2)(m1 + m2)
Then,
v2' = v12m1( m1 + m2) + v2 m1- m2 m1 + m2 …….. (iv) equation
Special cases:
There are some special cases in which the masses become equal or some are not equal but they have some target mass and their collision depends on them. Some cases are discussed below:
In the first case, the mass of both bodies m1 m2 is equal so that is why the is a mass exchange of both moving velocities after the collision.
To prove the above case we can use the equation (iii) and the equation (iv) which are given there.
Firstly we can use the equation (iii)
v1' = v1 ( m1- m2)( m1 + m2) + 2m2(m1 + m2)v2
According to this case, we know that m1 = m2 so,
v1' = v1 ( m- m)( m + m) + v2 2m(m + m)
v1' = v102m + v2 2m2m
v1' = 0 + v2
v1'= v2
According to this equation the velocity of the second mass exchange with the velocity of the first mass after collision.
Then use the equation (iv)
v2' = v12m1( m1 + m2) + v2 m1- m2 m1 + m2
In this case, we can also equal the m1 = m2 so,
v2' = v12m( m + m) + v2 m- m m + m
Then,
v2' = v12m2m + v2 0 2m
v2' = v1 +0
v2' = v1
According to this equation the velocity of the first mass exchange with the velocity of the second mass after collision.
In the second special case, the mass of both bodies is equal but the velocity of the second mass is also equal to zero.
To prove the above case we can use the equation (iii) and the equation (iv) which are given there.
Firstly we can use the equation (iii)
v1' = v1 ( m1- m2)( m1 + m2) + 2m2(m1 + m2)v2
According to this case, we know that m1 = m2, or v2= 0
v1' = v1 ( m- m)( m + m) + 0 2m(m + m)
v1' = 0 + 0
v1' = 0
According to this equation, the velocity of the second mass can be used by the first mass.
Then use the equation (iv)
v2' = v12m1( m1 + m2) + v2 m1- m2 m1 + m2
In this case, we can also equal the m1 = m2 or v2 = 0
v2' = v12m( m + m) + v2 m- m m + m
Then,
v2' = v12m2m + 0
v2' = v1
According to this equation, the velocity of the second mass after collision is equal to the velocity of the first mass before collision.
Elastic collision in two dimensions:
An elastic collision can occur in two dimensions. The motion or the elastic collision can be determined or understood through the law of conservation of momentum or the conservation of kinetic energy with the angular momentum. In the two-dimension collision, the first collision can occur in the ball line and the other occurs when the proper two moving bodies can collide hard. During this type of elastic collision, an angle can be created between them.
Derivation in which the two moving objects can collide with each other during the motion in two dimensions on the x-axis and the y-axis are given there:
To determine the elastic collision in the x-axis we can use the given formula,
v1x' = v1 cos (θ1 - φ) ( m1 - m2 ) + 2m2v2 cos (θ2 - φ)m1 + m2 cos θ + v1 sin (θ1 - ဖ ) cos φ + π2
To determine the elastic collision in the y-axis we can use the given formula,
v1x' = v1 cos (θ1 - φ) ( m1 - m2 ) + 2m2v2 cos (θ2 - φ)m1 + m2 sin θ + v1 sin (θ1 - ဖ ) sin φ + π2
These formulas can be used to determine the x and y-axis dimension motion of the bodies but if these motions can occur without the angles these formulas can be written as:
v1' = v1 - 2m2m1+ m2 (v1 - v2 , x1 - x2x1 - x22) (x1- x2)
Or,
v2' = v2 - 2m2m1+ m2 (v2 - v1 , x2 - x1x2 - x12) (x2- x1)
To determine the angles
For determination of the angle between in two-dimensional collision, we can use the given formula which can be written below:
tan θ1 = m2 sin θm1 + m2 cos θ
or,
θ2 = π - 02
To determine the magnitude of the moving bodies in two dimensions:
To determine the magnitude of the two moving bodies in two dimensions we can use formulas which are written below:
v1' = m12 + m22 + 2 m1m2 cos θm1 + m2
Or,
v2' = v1 2m1m1 + m2 sin θ2
Inelastic collision:
Inelastic collision is defined as:
“The kinetic energy that is not conserved during the collision is termed as the inelastic collision.”
In this type of collision the kinetic energy can be changed into other forms of energy due to the friction that can be produced when the two moving bodies collide hard and their kinetic energy can be changed into heat energy, sound energy, and potential energy.
Mathematical representation:
Inelastic collisions can be mathematically represented through the given equation.
m1 v1i + m2v2i = m1v1f' + m2 v2f'
Now, we know that in this type of collision kinetic energy cant be conversed so that's why it can be changed into different types of energy so it can be represented through the given equation which is written below:
12 m1 v1i2 + 12 m2 v2i2 12 m1 v1f2 + 12 m2 v2f2
Types of inelastic collision:
There are two main types of inelastic collision which are given there;
Perfectly inelastic collision
Partially inelastic collision
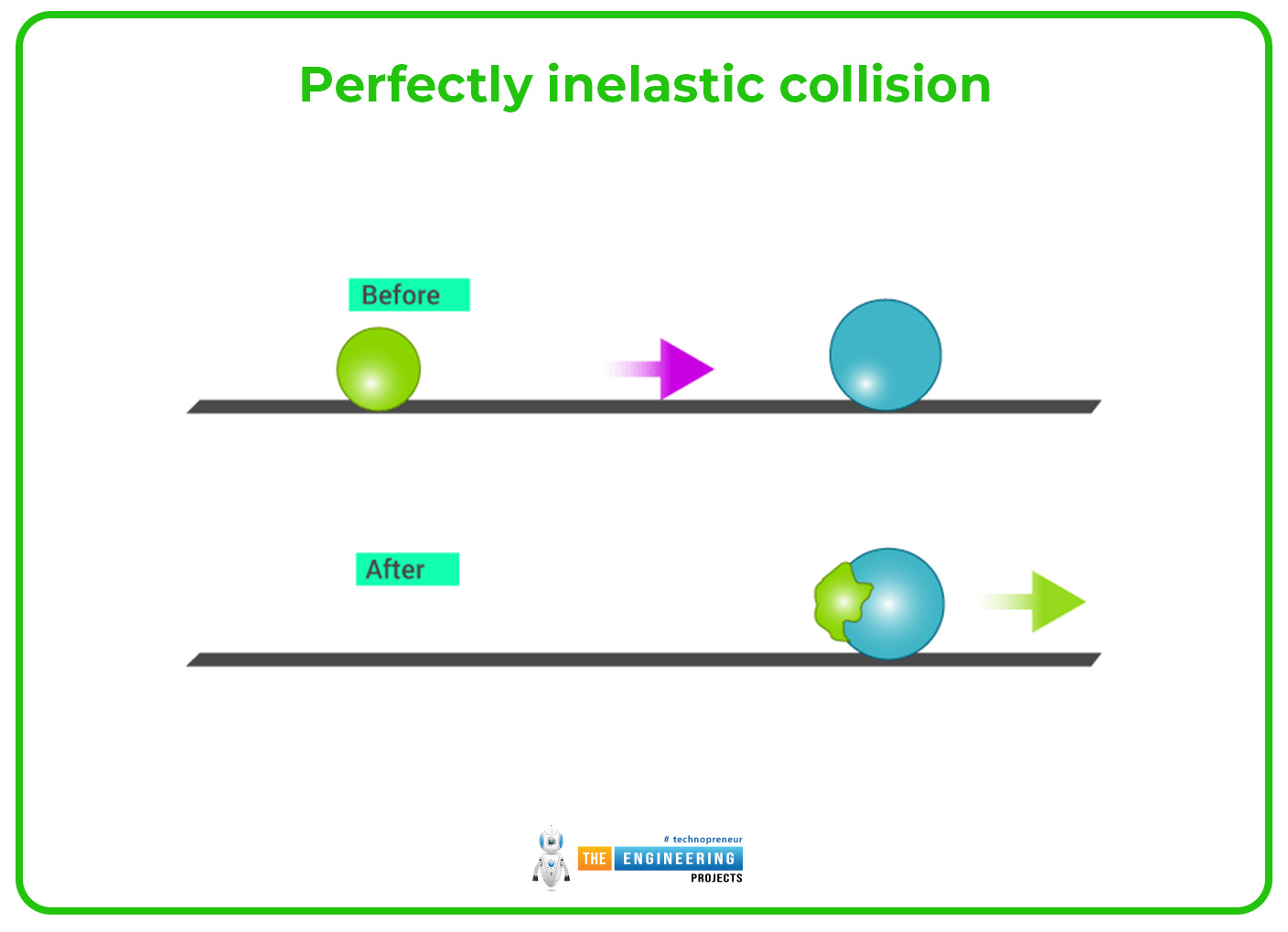
Perfectly inelastic collision:
In a perfectly inelastic collision, the two moving bodies that collide with each other are stuck together when they come closer for collision or they can't collide like the elastic collision. In this type of collision, the kinetic energy that is not to be conserved changes into other forms of energy totally as sound energy, heat energy, potential energy, and others.
Mathematically representation:
A perfectly inelastic collision can be represented through the given equation:
m1 v1i + m2v2i = (m1+ m2 ) vf'
Through this equation, it can be proved that the final velocity after the collision is the same for both masses because both moving bodies can be stuck together.
Partially inelastic collision:
In this type of inelastic collision, the moving bodies or masses can't stuck together but in this collision, most of the kinetic energy can not be conserved and change into different forms of energy but some kinetic energy may be conserved. In the real world or our surroundings, partially inelastic collisions occur because this type of collision is in the real world.
Examples of inelastic collision:
The some major examples of the inelastic collision are given there:
The car that can move on the road can collide with the other car then the kinetic energy that is produced during motion can be conserved somehow but mostly can be changed into another form of energy like heat energy, sound energy, and potential energy.
When the ball can collide with the soft floor then there kinetic energy can't be conserved so that's why it can't bounce back with high velocity.
Restitution coefficient:
The coefficient of the restitution which can be represented through the symbol e can be used to determine or describe the type of collision that can occur between the two moving bodies with the same mass or different velocities. It can simply defined through the given equation that can be written below:
e = relative velocity of seperationrelative velocity of approach
Or,
e = v2f- v1fv1i - v2i
This equation can be used for the determination of the type of collision between the objects such as;
- If e = 1 it indicates that the collision between the two bodies is elastic.
- If e = 0 then it indicates that the collision between the two bodies is perfectly inelastic.
- If 0 e 1 indicates that the collision between the two moving objects is partially inelastic
Conclusions:
To understand the conservation of energy or understand the concept of the interaction and the transferring of energy into another form, the concepts of elastic and inelastic collision are crucial to understanding because without understanding these concepts it can't be possible to understand the motion of two moving bodies efficiently. In the ideal system, both kinetic and momentum can be conserved but in reality, it can't be possible. In the real world mostly and commonly only partially inelastic collisions reoccurred. By understanding and reading the concept of collisions with their definitions, types, representations, derivations, and examples the reader can determine the types of collisions that can occur in their surroundings.



