What is KCL (Kirchhoff's Current Law)

Hello friends, I hope you all are doing great. In today’s tutorial, we will discuss What is KCL ( Kirchhoff's Current Law ). KCL (Kirchhoff's Current Law) is the fundamental rule of electric circuitries. In 1845 a German physicist Gustav Robert Kirchhoff presented two essentials rules to explain different circuitries. Ist law is KVL (Kirchhoff's Voltage Law) and 2nd is KCL (Kirchhoff's Current Law). These rules further defined the working of Georg Ohm, who gave Ohm’s Law and lead the work of James Maxwell who gave Maxwell equation. Both of these rules also work for a time (t) and frequency (f) measurements. In certain cases when the frequency of a signal is higher these laws work for the alternating current circuitries. In today’s post, we will have a look at its overview, working, example circuits and other parameters. So, let’s get started with a What is KCL (Kirchhoff's Current Law ).

What is KCL ( Kirchhoff's Current Law )

• KCL ( Kirchhoff's Current Law ) is also known as the ist rule of Kirchhoff. This law explains that current coming toward a point of the circuit is equal to the current moving away from that point in a circuitry.

?I = 0

• KCL is also named as conservation of charge because the current at the common point in circuitry remains reserve which means there is no loss of current at a point.
• Kirchhoff's Current Law is used to measure current in the different branches of any circuitry. How it finds current for this we explain a simple circuit.
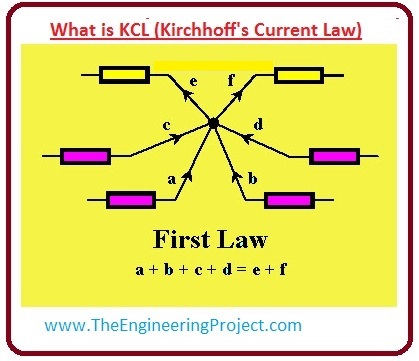
• In given circuitry you can see that the there are six branches of circuitry which are connected with the common point, this common point is also known as a node.
• In this circuitry, the direction of current in these six branches is denoted by a, b, c, d, e, and f.
• As we discussed earlier KCL says that current coming toward a point is taken positive and moving away negative. You can see in the circuit that the currents (a, b, c, d) are coming toward the common point so these will be taken positive and current (e, f) will be negative as they are moving away from the point.
• If we apply KCL to this circuit then the resultant equation will be.

a+b+c+d=e+f

Working of KCL( Kirchhoff's Current Law )

• Now we discuss how this law works for this we explain the given below simple circuit. Let's discuss it.
• In this circuit we can see that there is a node which has four wires connected with it, the current is passing through every wire.
• If we apply the KCL to the circuit then the equation of this circuit is

(I1)+(I2)–(I3)–(I4)=0

• This equation can also write to describe the inward current to the node and moving away from the current for the node.

(I1)+(I2)=(I3)+(I4)

• This equation shows that (I1) and (I2) is coming toward the node and the (I3) and (I4) moving away from the node.
• To the easy understanding of this law, we relate this given circuit with the liquid circuitry.

• Let's suppose we have a pipe in which liquid is moving with the rate of flow (Q1).
• If we divide this pipe into 3 smaller tubes, then the rate of flow of coming liquid will be equal to the liquid moving away from the center point. To further understanding lets see a diagram of this liquid circuitry which is similar to the KCL.

(Q1) = (Q2) + (Q3) + (Q4)

Nodal Analysis

• This method used KCL to find the value of the voltage at the node and then calculate the values of current and voltage at any component of the circuit.
• There are some steps you should follow to apply this rule which described below.
• To apply this rule, first of all, you should find the no of nodes in a circuit and reference node.
• Then allocate current and its path to every discrete division (branch) of the nodes in the circuit.
• Apply KCL to every node of the circuit.
• Then make equations and resolve them to find the values of current (I) and voltage (V).
• Then find the values of current (I) and voltage (V) at every component of circuitry.

Example of Nodal Analysis

Now we discuss how nodal analysis works practically and have a relation with the KCL.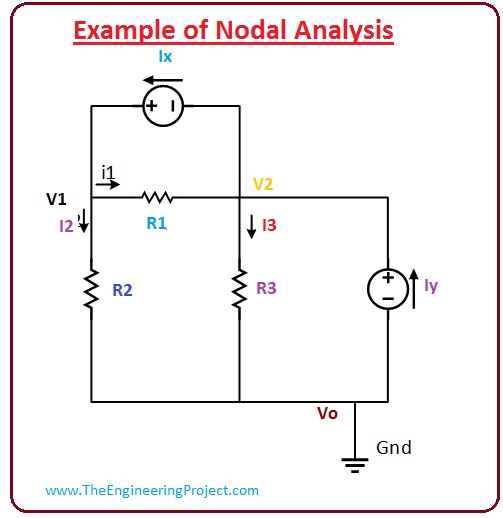

• The values of some elements which we know are given here.
  • Current Source (I_x)= (5 Amperes)
  • Current Source (I_y)= (10 Amerces)
  • Resistance (R₁) = (4 Ohms)
  • Resistance (R₂) = (2 Ohms)
  • Resistance (R₃) = (6 Ohms)
• First of all, we find the reference node in this circuitry, we consider V₀ as a reference node because it is joined with the ground terminal.
• As we know at ground potential is 0 so this will make our calculation simple.
• You can see there are three nodes in this node first one (V1), 2nd is (V2) and third is V₀ which is our reference node.
• Now we use KCL on a node (V₁) and node (V2) to find their equations.
• The equation for the first node will be.

(I_x ) = (I_{1 +} I₂₎

(I_y)= (I₃ – I₁)

• Now we put values of known elements of circuitry.

(5 A) = (I_{1 +} I₂₎ – (A)

(10 A) = (I₃ – I₁)- (B)

• You can see from the figure that there are three unknown currents is moving in this circuitry (I₁, I₂, I₃) we use ohm’s law to find their equations.

(I₁)= (V_1-V2)/R₂

(I₂)= (V₁-0)/ R₂

(I₃)= (V₂-0)R₃

• Now we put these current values in equation A and B.
• First we put these values in equation A.

5 = (V₁-V2)/R₂ + (V₁)/ R₂

5= (V1-V2)/4 + (V₁)/ 2

5 = (V₁ - V₂ +2V₁)/(4)

20 =3V₁ – V2 - (C)

• Now we will put the values of (I₁,I₂, I₃) in equation B and make resultant equation.

10= (V₁)/ R₃ - (V₁-V2)/R₁

10=(V₁)/ 6 - (V₁-V2)/4

10= (2v₁-3V₁ + 3V₂)/12

120= -V₁ + 3V₂ – (D)

• Solving equations C and D we have the values of V₁ and V2.

V₁ = 22.5v

V₂ = 47.5V

• Now we use these values and find the (I₁,I₂, I₃).

(I₁)= (22.5- 47.5V)/4

(I₁)= (-6.25A)

(I₂)= (V₁)/ R₂

(I₂)= (22.5)/ 2

(I₂)=11.5

(I₃)= (V₂)R₃

(I₃)= (47.5)/6

(I₃)= 7.91 A

Applications of KCL Law

• These are some applications of this law.
  • KCL is used to find the different electrical parameter like current, voltage and resistance in different circuits but it mostly used in complex circuits to find electrical parameters.

It was a detailed article on KCL law I tried my best to write in a simple way. If you have any question about it ask in comments. I will guide you comprehensively. Thanks for reading. Take care until the next tutorial.