What is Star Delta Transformation

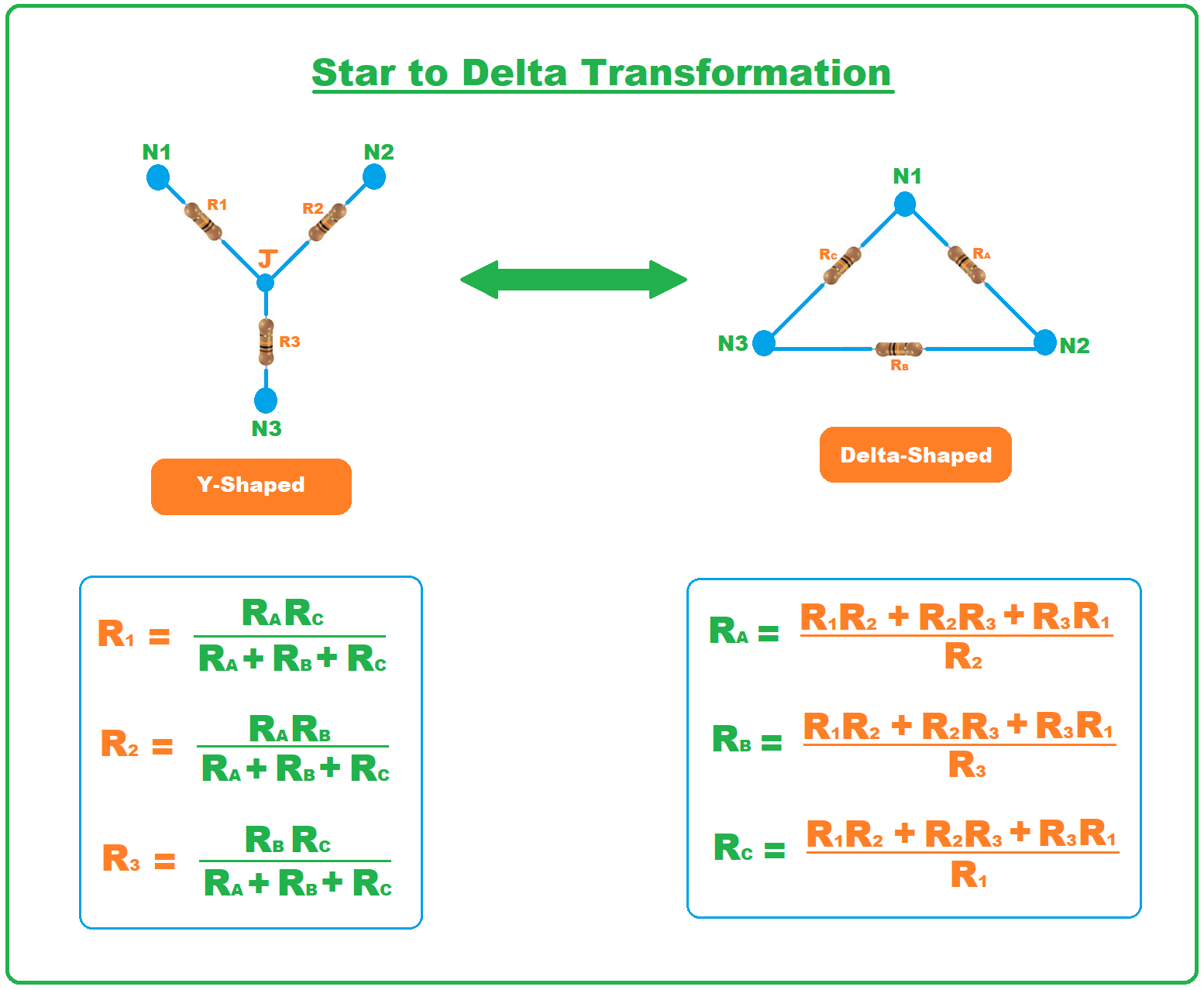
The star to delta transformation can also be expressed as Y-? transformation, it is a mathematical method used to solve complex resistive circuits in 3-phase electrical systems. Its name wye-delta is given to it because of its design. As shown in the figure, Star(wye) looks like Y, while Delta looks like ?.  This transformation technique from one form to another was given by Edwin Kennelly in 1899, who was an electrical engineer who belongs to the USA. Besides using in electrical circuitries star-delta transformation can also be used in maths to solve different planer graphs. In today’s post, we will have a look at its working, formula, equation, and uses. So, let’s get started with what is star-delta transformation?

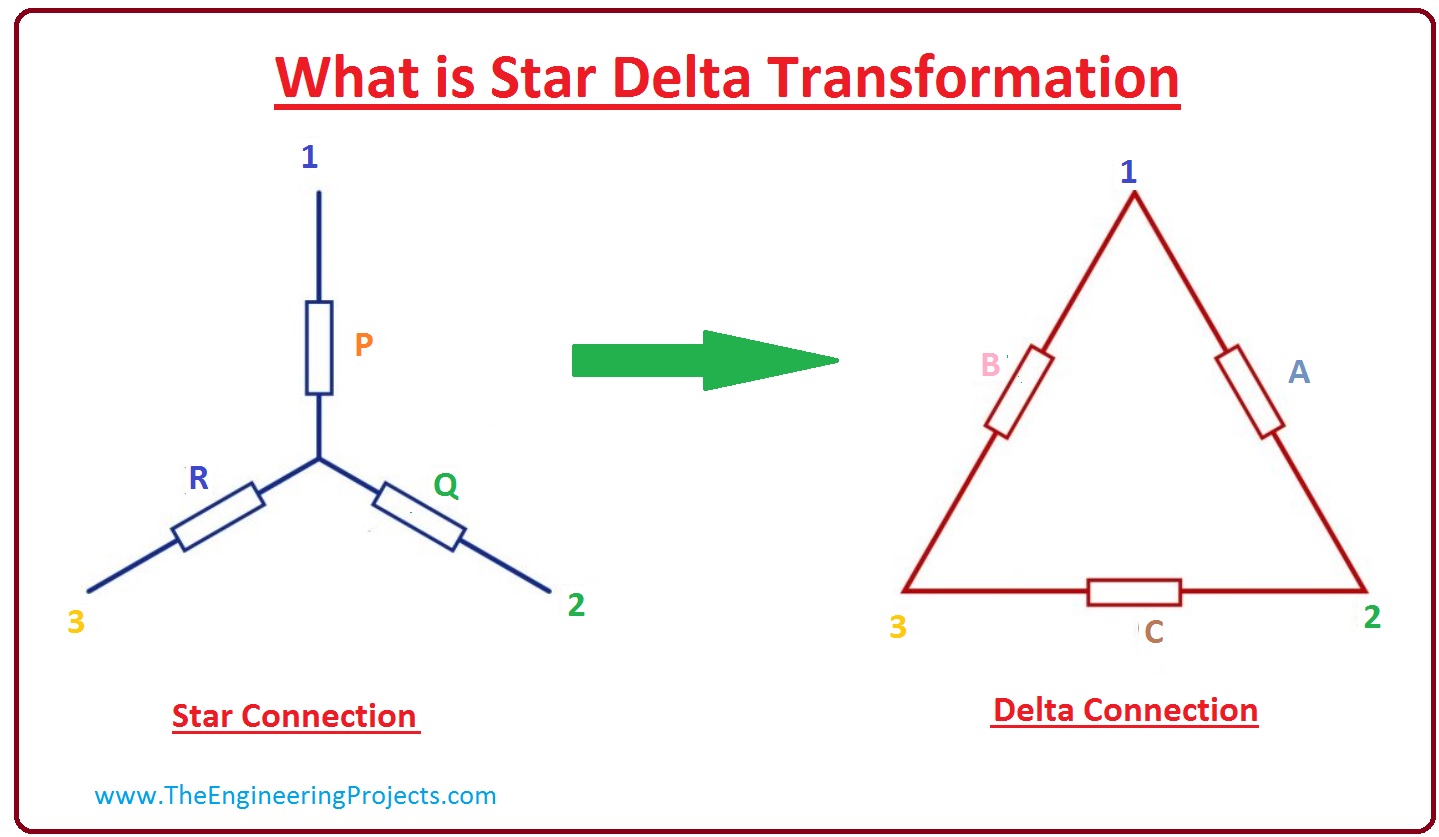
What is Star Delta Transformation?

• The Star-Delta Transformation (Y-?) is a mathematical technique given by Edwin Kennelly in 1899 and is used to solve complex 3-phase resistive electrical circuits by transforming from Star(Y) design to Delta(?) design with the help of formulas.

Before going any further, let's first understand why we need Star to Delta Transformation?

Why Star Delta Transformation?

• We use Star-Delta transformation to simplify complex 3-phase circuits.
• These simplified versions are a lot easier to solve as compared to the original complex ones.
• So, such transformations actually save us from complex calculations, thus reduce errors & save time.

Now let's have a look at Star & Delta arrangements, one by one:

What is Star(Y) Network?

• If all resistances are connected to a common point(also called Joint) from one end, while the other end(of the resistances) is open, this connection styling is termed as Star Network or Y Connection(also called wye circuitry).
• Star Connection is also referred to as open-loop as there's no loop in it.
• Below figure shows the T-Shaped Normal circuit and its equivalent Y-Shaped Connection:

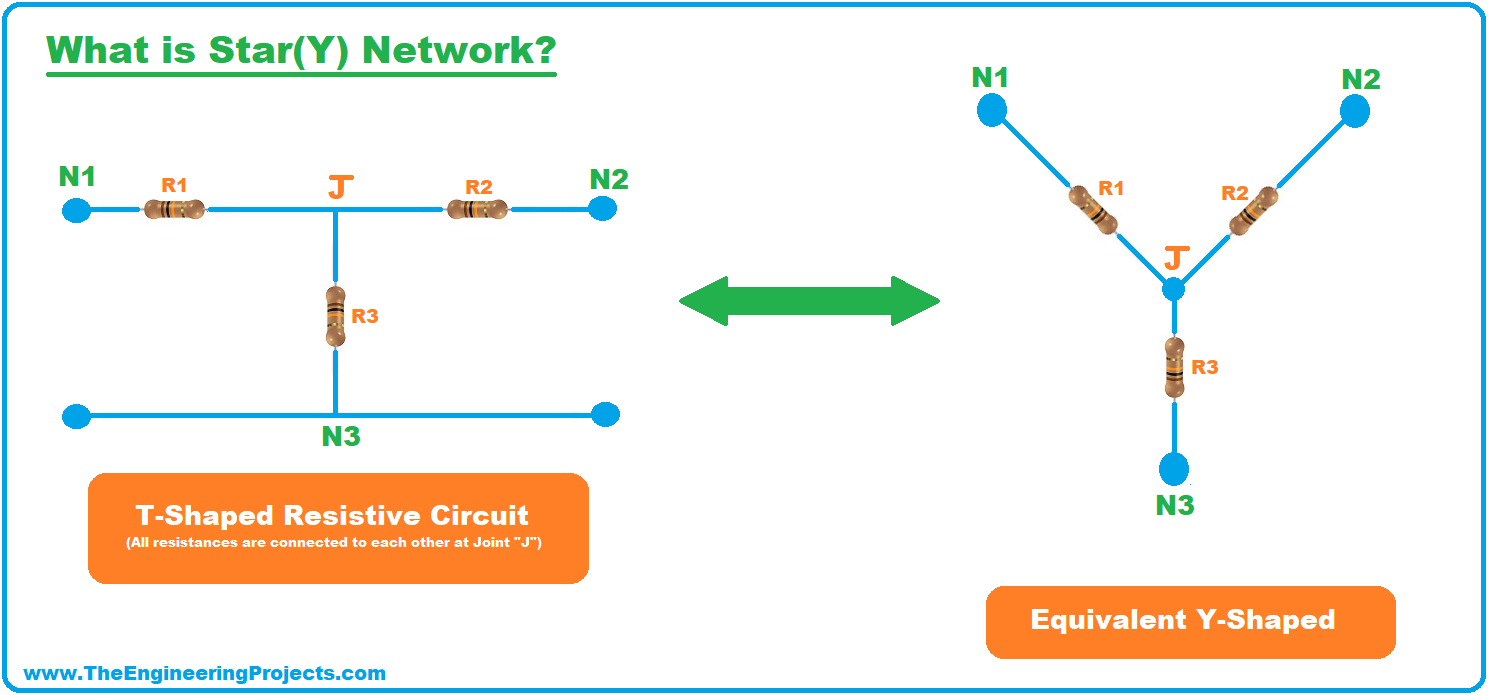
• We haven't performed any transformation in the above figure, instead, we have just draw a single circuit in two different styles, one is called T-shaped, while the second one is Y-shaped.
• In both of these forms, resistances are connected at a single common point called Junction/Joint, represented by J in the above figure.

Now let's have a look at How Delta Network looks like?

What is Delta(?) Network?

• If the resistances are creating a loop i.e. each end of resistance is connected to other resistance, such circuitry is termed as Delta Circuitry, Delta Network or Delta Connection, denoted by ?.
• Delta Connection is also referred to as a closed-loop as it involves a loop.
• Below figure shows the normal loop circuit and its equivalent Delta Circuit:

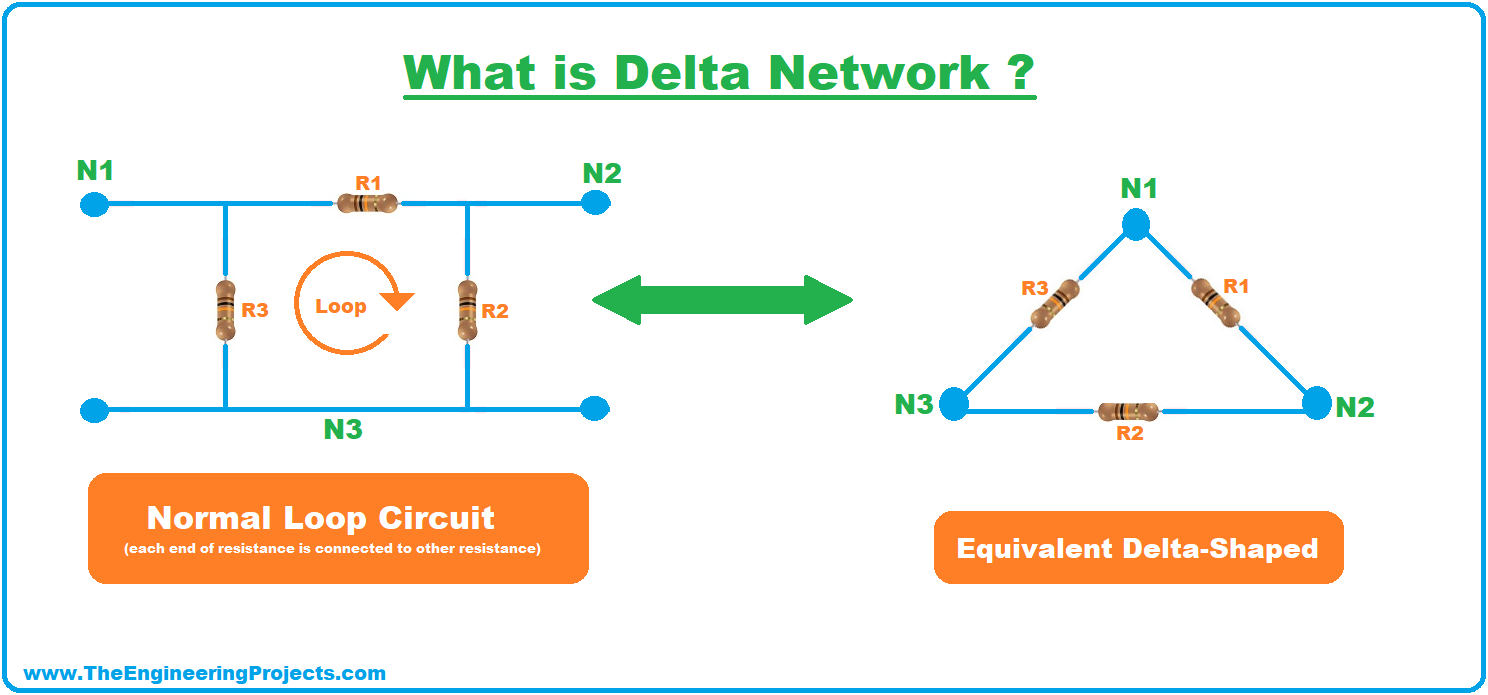
• Again we are not performing any transformation, instead, we are just displaying a single circuit in its two equivalent shapes.
• In both formats, resistances have created a loop and are connected to one another.

By now, you must have understood the difference between Star & Delta Connection and if you are presented with a circuit, you can easily find whether its a Star or a Delta. Now let's have a look at How to transform from one shape to another(i.e. Star to Delta & Delta to Star).

Star to Delta Transformation

• Transforming a circuit from Star Connection to Delta Connection is called Star to Delta Transformation.
• As shown in the below figure, both connections have the same number of resistances but their values are different.
• So, if we want to convert a Star Connection into a Delta one, then we need to find the values of all Delta resistances i.e. R_A, R_B & R_C.

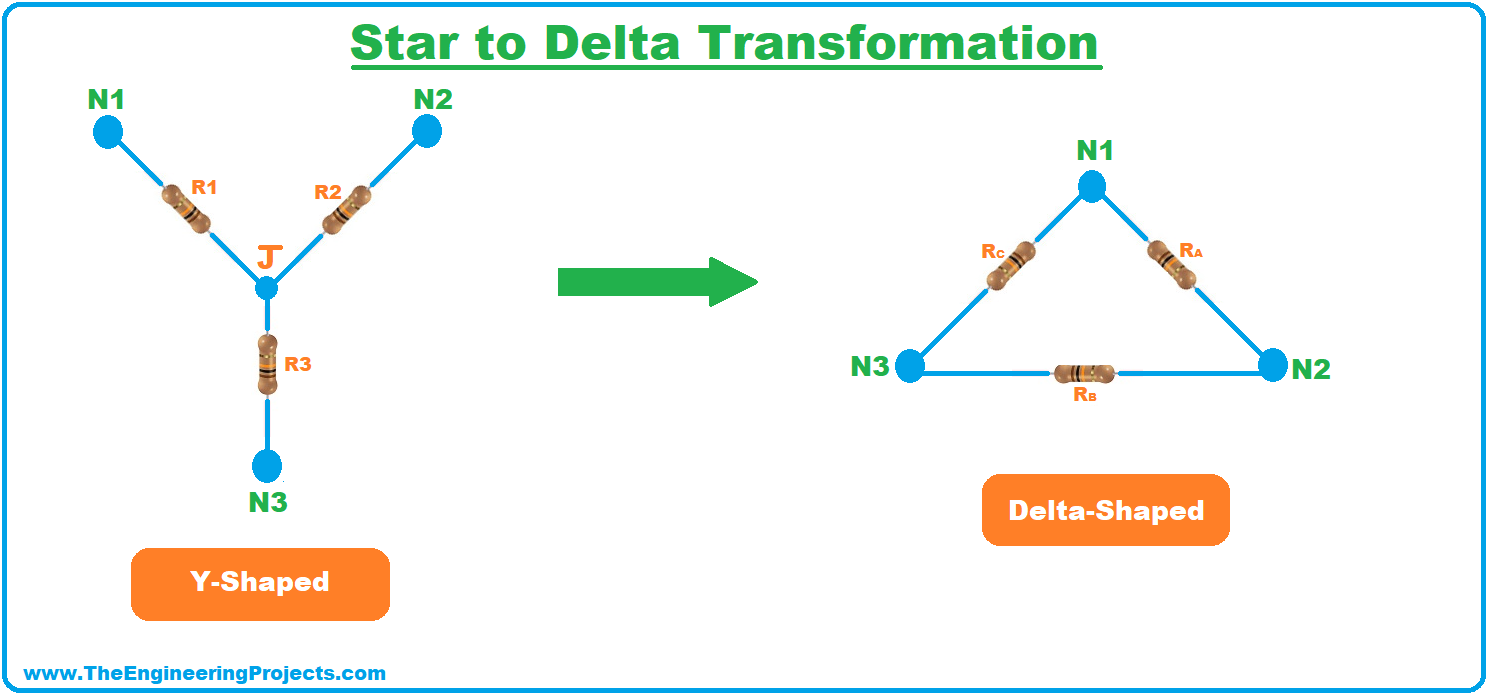
So, let's have a look at How to drive equations for Star Delta Transformation.

Equation of Star Delta Transformation

• As shown in the above figure, we need to find the values of Delta resistances.
• In order to do so, let's find out the resistance between nodes.

• In star connection, the resistance between N1 & N2 is equal to R₁ + R₂.
• In Delta connection, resistance R_A is in parallel with R_B & R_C, so the resistance between N1 and N2 will be equal to R_A(R_B + R_C)/(R_A + R_B + R_C).  (using resistance parallel formula)
• As both circuits are equivalent, so the resistance between similar nodes must be equal and will give us equation A, shown below:

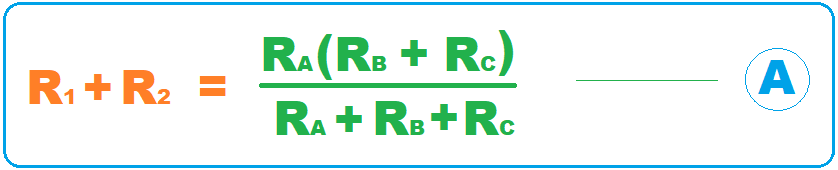
• The resistance between nodes N2 & N3 will give us equation B:

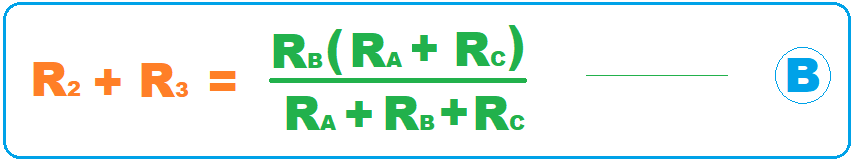
• The resistance between nodes N3 & N1 will give us equation C:

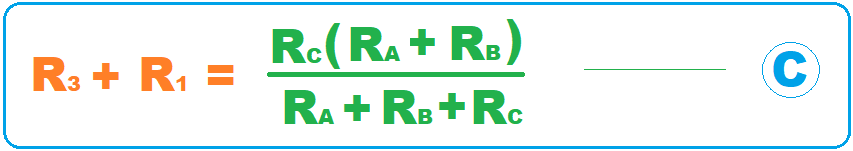
• Now let's add Equations A, B & C and we will get equation D, as shown in the below figure:

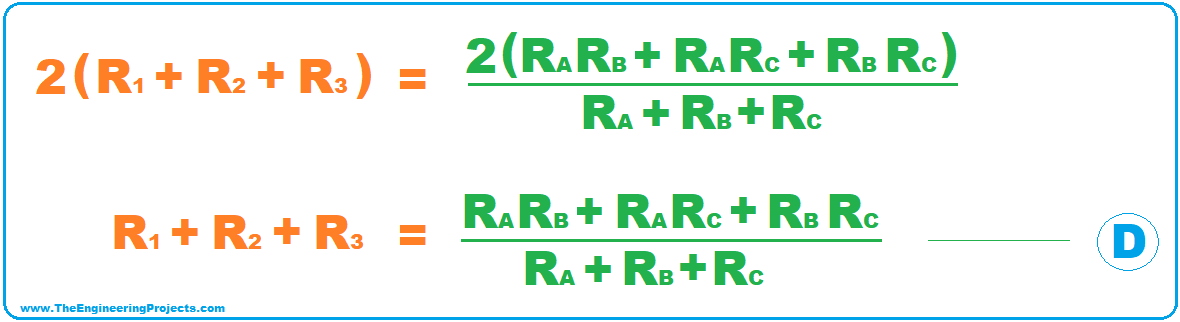
• Now let's subtract equations A, B & C from equation D and we will get values of R₁, R₂ & R₃, as shown in the below figure:

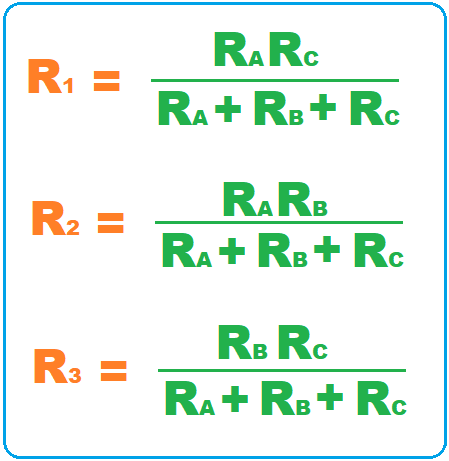
• Now by using these values of R₁, R₂ & R₃, we can get the value of R_A, R_B & R_C, as shown in the below figure:

• So, using these six equations, we can easily convert Star to Delta and Delta to Star, it will get more clear when we solve examples in the next section.

Example of Star Delta Transformation

• The star-? alteration complications are the finest samples to comprehend the idea of the circuitries.
• The resistance in a star system is represented with (X, Y, Z), which can be seen in the above diagram and the values of these resistances are (X= 80?), (Y= 120?), and (Z = 40?).

A= (XY/Z) +Y+X)

X= 80 ?, Y= 120 ?, and Z = 40 ?

• By putting these parameters in the above formula we calculate the value of A.

A = (80 X 120/40) + 120 + 80 )= (240 + 120 + 80 )= (440 ?)

• As we have find value of resistance (B) which is ((ZX/Y) + X+Z).
• Now we put values in this equation to find the value of B.

B = ((40X80/120) + 80 + 40) = (27 + 120) = (147 ?).

• Now we can calculate the value of resistance C by this equation

C= ((YZ/X) +Z+Y)

• Putting value in this equation we get C.

 ((120 x 40/80) + 40 + 120) = (60 + 160) = (220 ?)

Delta To Star Transformation

• Now we see how we can converts delta circuitry back to the star connection.
• Let's solve circuitry which is connected in the delta form and has 3 points a, b, c. The value of resistance among the joints a and b is (R1), resistance among the b and c is (R2), and c and d are (R3).

  

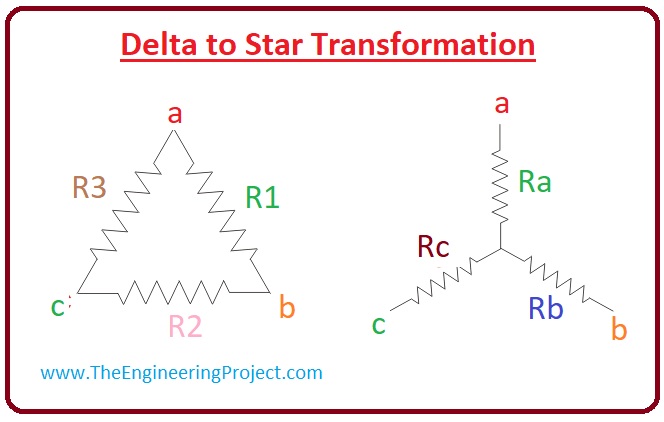
• The value of resistance among the points and b is given here.

(Rab) = (R1)??(R1+R2)

= [(R1).(R2+R3)]/[(R1+R2+R3)]

• You can see there is another circuitry that is connected in the Y connection it has three branches a, a, c which has resistance (Ra, Rb, Rc).
• If we find the resistance among points a and b then we have.

(Rab) = (Ra+Rb)

• As both of these circuitries are equivalent so the value of resistance is measured among points a and b.

(Ra+Rb)=[(R1). (R2+R3)]/(R1+R2+R3)----(x)

• So the resistance values will also same in the among points b and c.

(Rb + Rc)=[(R2). (R3+R1)]/(R1+R2+R3)---(y)

• And the value of resistance among the c and a will also same.

(Rc + Ra)=[(R3) x (R1+R2)]/(R1+R2+R3)---(z)

• If we add expressions  (x),(y),(z) then we have.

(2)(R1+R2+R3)= 2[(R1.R2)+(R2.R3)+(R3.R1)]

(R1+R2+R3) =[(R1.R2)+(R2.R3)+(R3.R1)]/[(R1+R2+R3)]----(d)

• If we subtract the equation (x),(y), (z) from equation (d) then we have.

Ra =(R3.R1)/(R1+R2+R3)---(e)

Rb =(R1.R2)/(R1+R2+R3)---(f)

Rc=(R2.R3)/(R1+R2+R3)--(g)

• The expression of the Y-? transformation can be defined as.
• From equations e,f,g we can conclude that the resistance in star configuration is equivalent to the multiple of the 2 resistors joined with the identical point divided by the sum of all resistors in the ? circuitry.
• If in the delta circuitry the values of all resistors are identical then the correspondent resistance value (r) in the star circuit will be.

r = (R.R)/(R+R+R)

r= R/3

Advantage of Star Delta Conversion

• These are some advantages of this transformation which are described here.
  • Star transformation is well suitable for transport voltages to long distances and it also has a neutral point that can be used to the unbalanced transient current of the circuitry to the ground.
  • Delta transformation can transport balance three-phase voltage(V) without any neutral (n) wire which marks ? best for Transmission network.

It was a detailed article on Star Delta transformation if you have any questions about it ask in the comments. Take care until the next tutorial.