Properties of Fluid

In the introduction, I will extensively explain the property r and how to impact them are so. Let us start. Then I explain properties that are related to fluid flow.

First of all, I will start with the word Property. The definition of property is as follows:

Property

The word property is defined as any characteristic of the system. There are two main types of the property named intensive and extensive.

Example

The examples of property are as follows

• Temperature -T

• Pressure - P

• Mass – m

Types of Properties 

Following is a brief explanation of the types of properties.

Intensive Property

The intensive properties are the ones that are independent of mass, temperature, density, and pressure. Therefore, they are presented in lowercase letters. But here stands an exceptional case, i.e., the temperature and pressure are only denoted with uppercase letters.

Example

The examples of intensive property are as follows:

• Velocity - v

• Specific Internal Energy - u

• Temperature - T

• Charge Density - ne or ρ

• Molality - m or b

Extensive Property

The extensive property is the ones that depend on the size or extent of the system. They are presented by the uppercase letter, but here is an exceptional case for the mass presented by a lowercase letter. 

Example

Extensive properties are usually derived, so the following are some examples.

• Total Energy

e= E/m

• Specific Volume 

v=V/m

Specific Property 

The specific property is the ones that depend on that are derived from either extensive or intensive ones. 

Example

One of the simple examples of a specific property is the density of water; as we know, it is an intensive property. So the extensive property (derived ones) is the mass of water volume divided by the volume. Here both the mass of water and volume are extensive properties.

Continuum

The term continuum is related to matter in this way: the matter is made of atoms, and their distance and compactness vary from state to state. As in solids, atoms are closely packed, whereas, in liquids, there is some distance. However, in gases, the atoms are spaced widely. So in the continuum, the matter is defined as continuous and homogenous with no holes. 

The primary purpose of using a continuum is to treat properties as a point function, and there are no jump discontinuities as the properties vary in space continually. This only applies when the system size is large compared to the space in molecules. It is practically applicable in almost every case except exceptional cases.

Properties related to fluid flow

At the start of the discussion, I discussed the properties such as intensive and extensive observed during the fluid flow. Now some more properties play a distinct role in the fluid flow and their importance. So without wasting any time, let’s start.

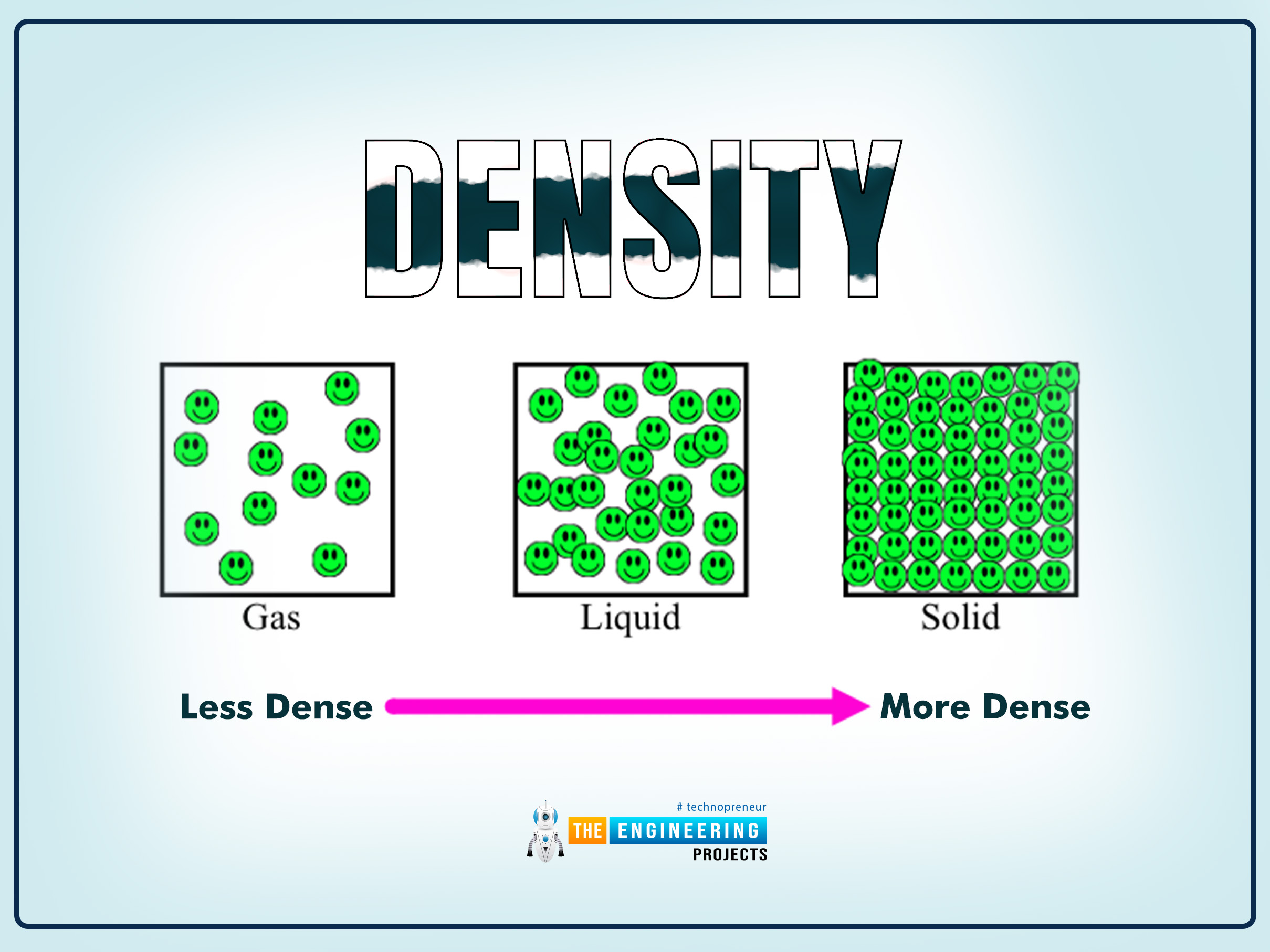
1. Density

The density is defined as;

Density is mass per unit volume.

Formula:

ρ=m

Specific Density

It is defined as 

The specific density is the reciprocal of density, i.e., volume per unit mass. 

Formula:

υ=Vm

Factors affecting Density

There are numerous factors on which the density depends. The most important of all is the temperature and the pressure, which change the nature of the substance. 

Gases

In gases, an increase in pressure will decrease the temperature and vice versa.

Solids and Liquids

Compared to gases, solids and liquids are incompressible, so an increase or decrease in pressure is negligible. 

Example 

In solids and liquids, the temperature is an essential factor that changes the density compared to the pressure. For instance, at the pressure of 1atm, the density of water changes from 998kg/m3 to 975kg/m3. So the difference is about 2.3 percent which is negligible in many cases.

Relative Density or Specific Gravity

The definition is as follows:

The density of the substance is relative to the density of the well-known substance.

Formula:

SG=H2O

SI units of Specific Gravity

As relative gravity is a dimensionless quantity, so the SI unit of it is as same as the density one, i.e., kg/L or g/cm3 (0.001 times density in kg/m3)

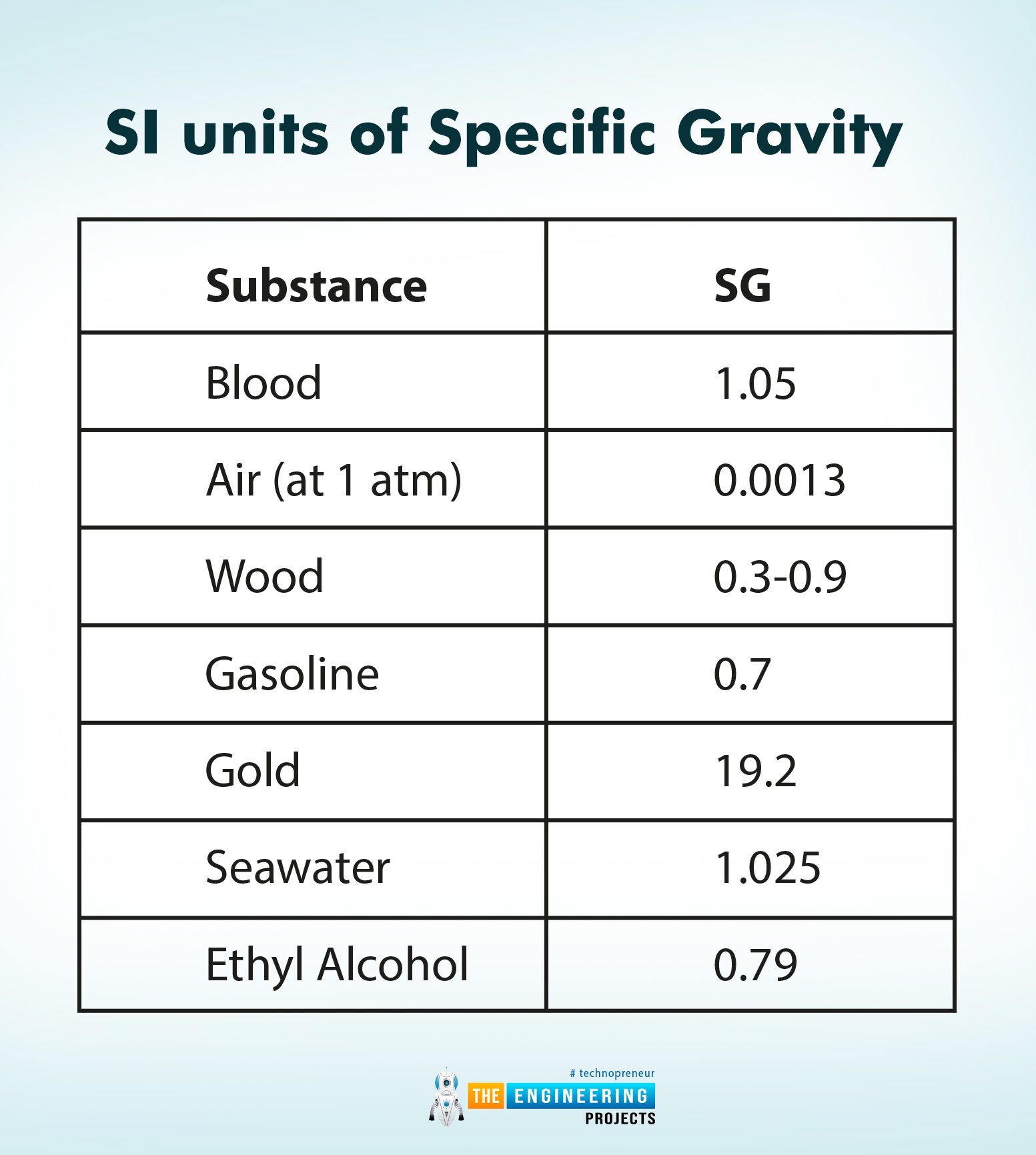
Specific Gravity of Substances

The following is the list of some substances with specific gravity at 0˚C.

Specific Weight

The definition of specific weight is as follows:

The weight of a unit volume of a substance is known as specific weight.

Formula

s=ρg

Vapor Pressure and Cavitation

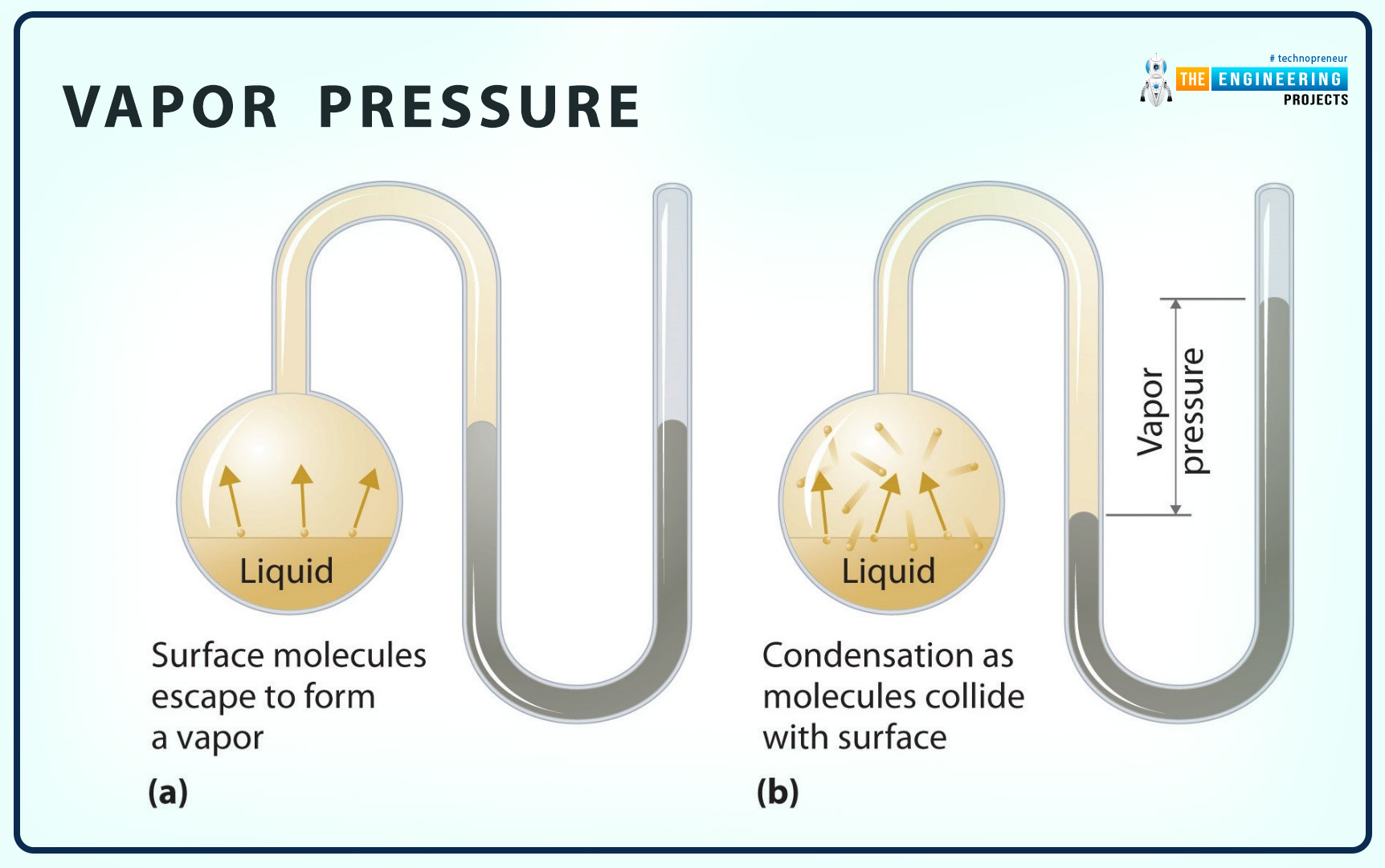
Vapor Pressure

The definition of vapor pressure is as follows:

Vapor pressure is the pressure applied by the vapor of a pure substance at the state of equilibrium with its liquid at a given temperature.

Some important key points related to the vapor pressure are as follows:

• It is presented by Pv.

• Vapor pressure is as same as saturation pressure Pv.=Psat.

• Sometimes, vapor and partial pressure are considered one thing, but they have two different definitions and applications. 

• Increase in temperature increases the vapor pressure.

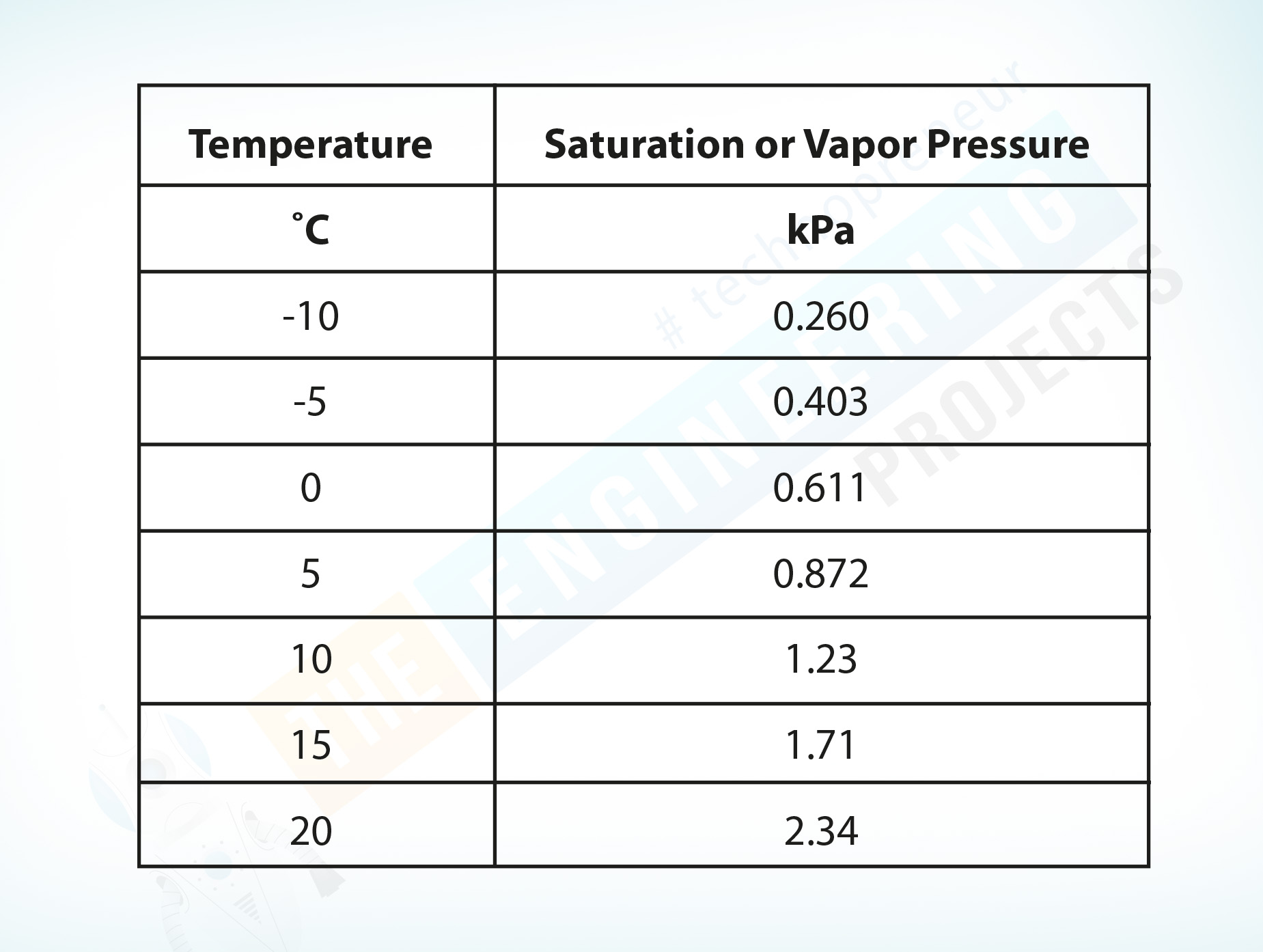
The following table shows water saturation or vapor pressure at different temperatures.

Some important terms are related to vapor pressure, and they are named saturation temperature and saturation pressure, respectively. 

• Saturation pressure is the pressure at which changes in the state of a pure substance occur at a given temperature. It is represented by Psat.

• Saturation temperature is the temperature at which changes in the state of a pure substance occur at a given pressure. It is represented by Tsat.

Partial Pressure

The definition of partial pressure is as follows:

Partial pressure is the pressure of gas or vapors with a combination mixture of gases.

Some important key points related to partial pressure:

• Partial pressure of water vapors has some atmospheric pressure, and the value is 0.3. 

• The absence of liquid equalized or less than the partial pressure of vapors to the vapor pressure. 

• At the state of equilibrium, the presence of partial and vapor pressure in the system then the system is saturated.

• In open lakes, the evaporation rate is managed by the vapor and partial pressure differences.

Cavitation

As we know, vapor bubbles in the liquid collapse when they are moved or swept from low regions. The result is the production of high-pressure waves that creates destruction. The reason for explaining this is that the phenomenon is related to cavitation, and the vapor bubbles formed are called cavitation bubbles. The phenomenon mentioned above is called cavitation as it is the leading cause of destruction and causes performance to drop off.

Some important key points related to cavitation:

• In designing hydraulics pumps and turbines, this phenomenon (cavitation) is prioritized

• In flow systems, cavitation is not considered as they result in poor performance, turbulence and noise.

• For checking whether cavitation is present in the flow system or not, cavitation is observed by a unique tumbling sound.

Energy and Specific Heat

We are well known for the term that energy cannot be created nor destroyed but can be transformed from one form to another. There is various form of energy that we observe in our daily life. 

So I will recall some of the vital energy that is used during the fluid flow:

Kinetic Energy

The basic concept of kinetic energy is that anybody or system (comprised of energy) is in motion relative to the reference frame and is said to have kinetic energy. 

Formula:

K.E = 12v2

• Here, v stands for the velocity of the system or body relative to the reference frame.

Potential Energy

The potential energy is the energy possessed by the body or system due to elevation in the gravitational field.

Formula:

P.E =gz

• Here, g represents the gravitational acceleration, whereas z represents the elevation of the system or body concerning the reference position. 

Thermal Energy

Thermal energy is the energy that is related to the temperature. So it is defined as the energy in the system responsible for temperature.

Formula

Q=c ∆T

• Here ∆T represents the temperature difference, whereas c represents the specific heat.

After discussing all the energy, one important term related to fluid flow is the Enthalpy. So let us discuss enthalpy.

Enthalpy

The enthalpy is the combination of internal energy and the product of volume and pressure. The enthalpy value is calculated with the help of pressure, temperature, and volume, respectively. The energy conservation law says that internal energy changes equal heat transfer. The enthalpy change is assumed to equal the heat transfer if the work changes the volume at constant pressure.

Formula:

H=E +PV

• Here, H is the enthalpy, E stands for internal energy, P stands for pressure, and V stands for the system volume.

Total Energy

The sum of all the energy of flowing fluid is called total energy. 

Formula

eflowing=K.E+P.E+Enthalpy

eflowing=h+V22+gz

Coefficient of Compressibility

There is an expansion in fluids when they are heated, and they contract when they are cooled. This means that temperature and pressure are two essential parameters responsible for contraction and expansion. The temperature and pressure also change the volume or density of the fluids. But volume or density varies differently from fluid to fluid. So, two properties are related to the volume or density changes to the change in pressure. And they are named Bulk Modulus of Elasticity and Coefficient of volume expansion.

So let’s explain these two properties without wasting any time.

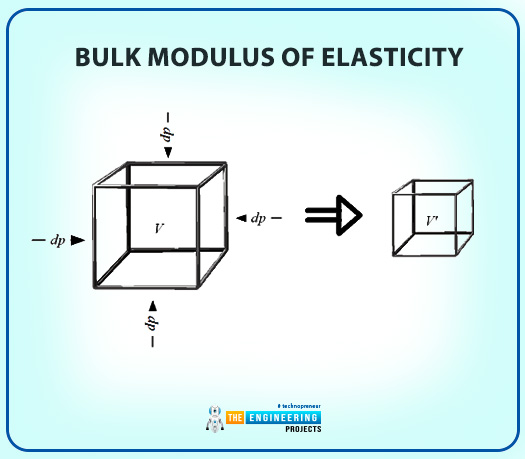
Bulk Modulus of Elasticity

There is a similarity in solids’ and liquids' expansion and contraction principles. So, the definition of the bulk modulus is as follows:

Bulk Modulus of Elasticity is a property that is the ratio of change in pressure relative to the volume.

Formula:

κ = -v(Pv)T= ρ(P∂ρ)T     (1)

The formula can also be presented concerning the finite changes, as shown below.

κ≅ -∆P∆vv≅-∆P∆pp

• Here ∆vv and ∆pp are dimensionless. 

• The unit of κ is psi or Pa.

• Here, the temperature is kept constant, so the bulk modulus of elasticity presents the change in pressure to the change in volume and density of the fluid. 

• The above equation proves that the incompressible substance coefficient of compressibility (Bulk modulus of Elasticity) is infinite.

• Increase in pressure decreases the volume.

• The negative sign indicates Pv is a negative quantity, whereas the bulk modulus value is positive.

An important key point related to Bulk Modulus of Elasticity:

• Bulk modulus of elasticity is also known as the coefficient of compressibility or bulk modulus of compressibility.

• If the value of bulk modulus is significant, then firstly, the fluid is incompressible, and then a large amount of pressure is required for a small amount of fractional change in the volume.

• When the equation is being differentiated, then

• From the equation, it is evident an increase in one quantity decreases the other and vice versa. From equation 1, we will differentiate the ρ=1/v, and we will get dρ=-dv/v2. So after cancellation, the final result will be:

dρ=-dvv

• The inverse of the coefficient of compressibility is called isothermal compressibility. 

• The formula is as follows:

α=1=-1v(∂v∂P)T=1(∂ρ∂P)T

Coefficient of Volume Expansion

It is observed that there is a drastic change in liquid density when it is increased or decreased. A property named coefficient of volume expansion is responsible for the fluid density difference at constant pressure and variable temperature.

Formula:

𝛃=-1v(∂v∂T)P=-1(∂ρ∂T)P

• The coefficient of volume expansion is represented by beta.

• At the infinite changes, the formula is shown below:

-∆vv∆T=-∆pp∆T

• Here, the pressure is kept constant.

Important key points related to the coefficient of volume expansion:

• Increase in temperature increases the value of as they have a direct relationship.

• ∆T represents the temperature difference in the equation. 

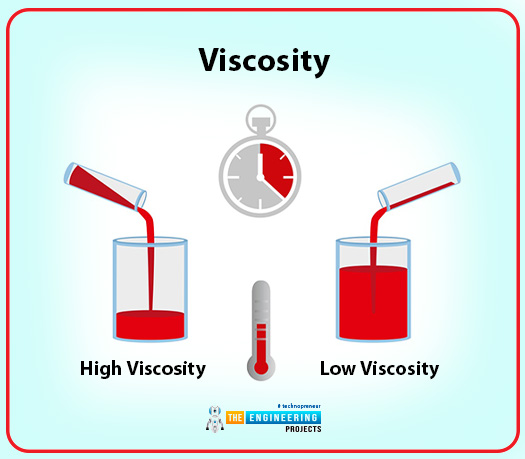
Viscosity

If we define viscosity, the most reasonable and appropriate term will be resistance. When the fluid flows, there exist layers of viscosity at that point. There are intermolecular forces in fluid when the fluid is more viscous. So the definition of viscosity will be:

Viscosity is a property that represents the internal resistance of a fluid to motion.

Example:

One of the best examples is the pouring of honey. As you observe, honey is dense and very has strong internal resistance.

Formula:

η=2ga2(∆ρ)9v

• We assume a sphere that is dropped onto the fluid, and then the fluid’s viscosity is measured.

• Here ∆ρ is the density difference between the fluid and surface

•  a is the radius of the sphere 

•  G is the acceleration due to gravity

Important key points related to viscosity:

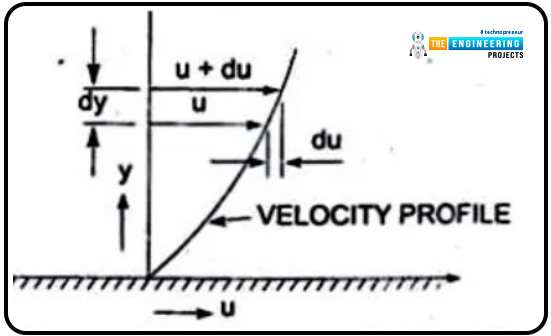
• When one layer moves adjacently to the other, some friction exists, which we named viscosity. The layers are moving at some distance and are named dy. The velocities of the fluids are u and u+du, respectively. 

• The graphical presentation of the layer velocity versus the distance is shown below.

• The graph will explain the trends of velocity and distance. As mentioned, two layers are moving adjacently to each other, so the layer that is on top imposes shear stress on the lower layer, and the lower layer, in response, causes shear stress on the upper one. 

Types of Viscosity

There are two primary types of viscosity, and they are explained briefly as follows.

Kinematic Viscosity 

Following are some essential key points related to kinematic viscosity:

• Kinematic viscosity is the ratio between dynamic viscosity and fluid density.

• The formula of kinematic viscosity is as follows:

υ=

Here υ is the kinematic viscosity η is the absolute or dynamic viscosity, and ρ is the density of the fluid.

• When the temperature decreases, kinematic viscosity also decreases.

Dynamic or Absolute Viscosity

Following are some essential key points related to dynamic or absolute viscosity:

• Dynamic viscosity is the ratio of shear stress to the shear strain of motion.

• Dynamics viscosity helps in the interaction of the molecules dealing with mechanical stress.

Conclusion:

I hope you enjoyed reading the article and have an extensive overview of the fluid-flowing properties. Thanks for reading.