As I have discussed the pressure now I will explain fluid mechanics. The definition of fluid mechanics is as follows:
Fluid mechanics deals with the properties and characteristics of fluid at rest.
Some of the important key points related to the fluid statics are as follows:
Fluid statics has many properties just as hydrostatics when the fluid is in a liquid state and acts as aerostatics when it is in a gaseous state.
The only stress that is in fluid statics is the normal ones other than that there is no shear stress.
The main application of fluid statics is to determine the forces that are acting on the floating or the submerged bodies.
That is a brief introduction to fluid statics further I will explain the forces that are acting on submerged and floating bodies. So without wasting any time let us start.
Hydrostatics Forces on submerged plane surfaces
The structure of the surface and the forces that are acting on the surface is explained as follows:
As the name suggests, there is a plane surface on which liquid flows and the surface is resting.
The fluid pressure is equally distributed onto the surface.
So the set of parallel forces is formed on the surface as a result of hydrostatics forces.
As one side of the surface is facing the fluid pressure whereas the other side is sometimes exposed to the atmosphere and as the result is zero resultant.
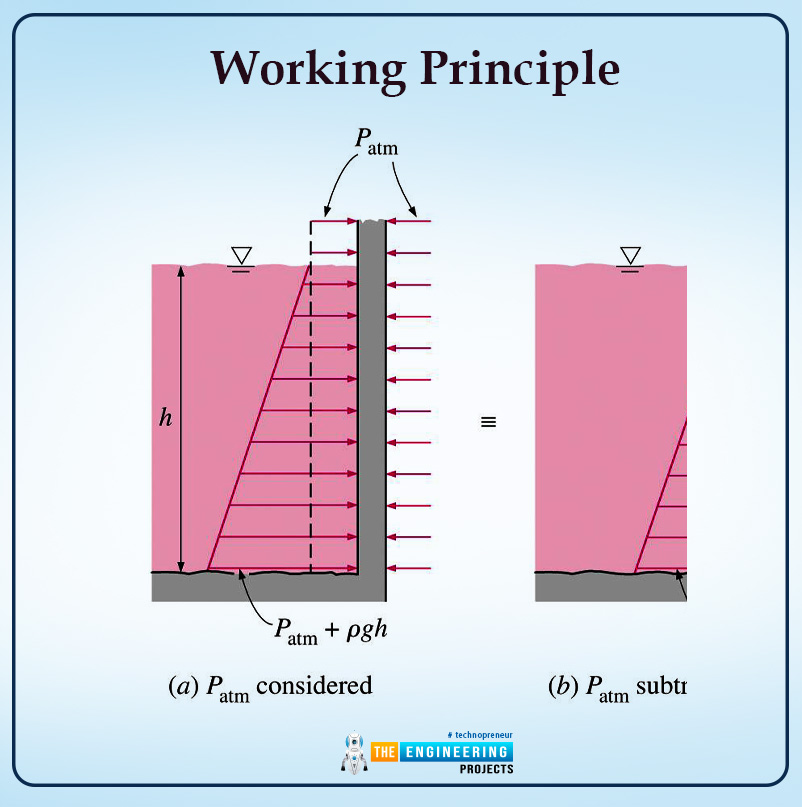
Working Principle
The working principle along with all the equations that are acting on the surface are explained as follows:
First of all, as I have discussed earlier that one side of the plate is completely exposed to the atmosphere and has atmospheric pressure whereas the other side of the plate is completely submerged in the fluid as shown in the diagram.

The horizontal surface intersects the plane surface at some angle so that line is considered to be x-axis.
Po is the absolute pressure i.e., the pressure that is above the fluid (liquid) also known to be local atmospheric pressure if the fluid or liquid is exposed to the atmosphere.
The equation of absolute pressure is:
P=P0+ρgh
P=P0+ρg ysinθ (equation 1)
Here h is the vertical distance of a specific point to a surface and y is the distance of a point from the x-axis from the point O as shown in the diagram.
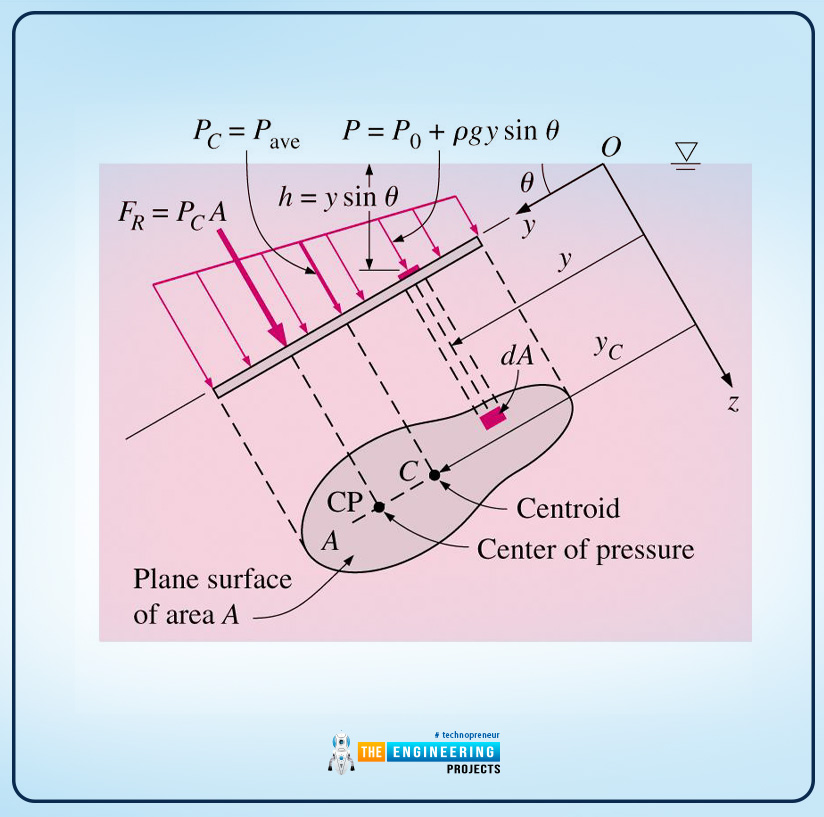
Now the next step is to find the resultant hydrostatics force and for that, the equation is as follows:
FR=∫APdA
Here we will substitute the value of P from equation 1 and equation 2 will look like this:
FR=∫A(P=P0+ρg ysinθ) dA
FR=P=P0A+ρg sinθ∫AydA
∫AydA is the first moment of the area as it is in the y-coordinate and the value is as follows:
yc=1A∫AydA
By substituting the value, we get the final result:
FR=P0A+ρgyc sinθA
FR=P0+ρghcA
FR=PcA
FR=PavgA
The final result will be stated theoretically:
The final resultant force is equal to the pressure at the centroid surface and the area.
Hydrostatic Forces on Submerged curved surfaces:
The structure of the surface and the forces that are acting on the surface is explained as follows:
As the name shows that the curved surface is submerged in liquid and the hydrostatic forces are determined.
In this part we have applied the integration of pressure forces that fluctuates when the direction of the surfaces changes.
The final force (resultant) is equal and opposite to the force that is acting on the curved surface.
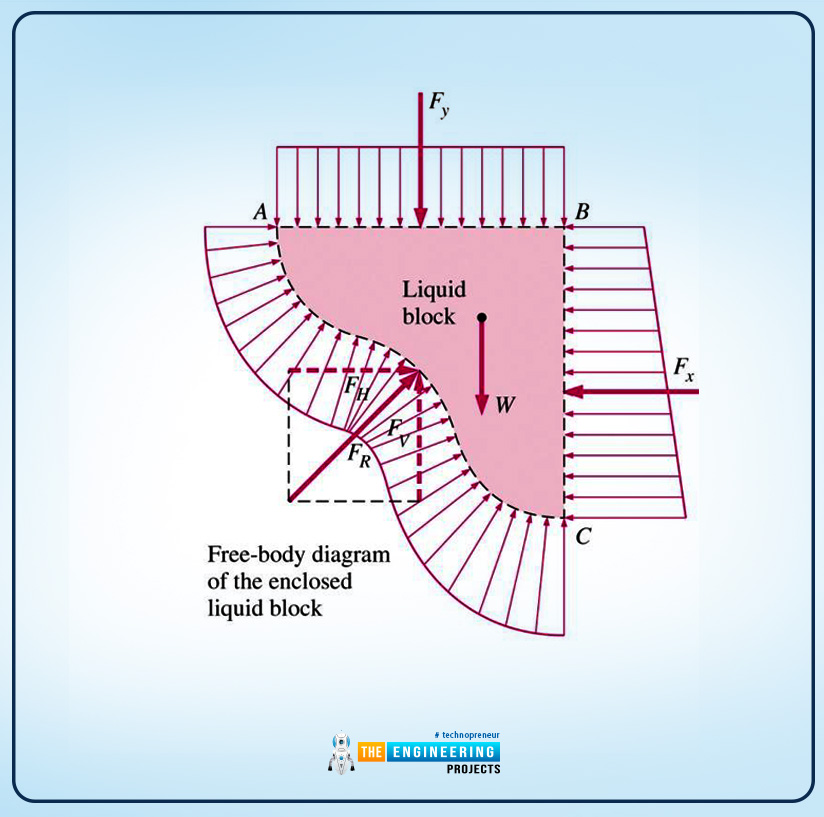
Working Principle
The working principle along with all the equations that are acting on the surface are explained as follows:
Here the weight of the enclosed liquid is as follows:
W=ρgυ
Here V is the volume of fluid and that is in a downward direction as shown in the figure.
the vertical and horizontal forces will be:
the horizontal force component on a curved surface:
FH=FX
the vertical force component on the curved surface
FV=Fy+W
The final result will be:
the horizontal and the vertical component of the hydrostatic force of a curved surface are both equal in case of magnitude and line of action.
The horizontal and vertical component is an equal hydrostatic forces acting on horizontal projection along with the weight of the fluid.
Conclusion:
I hope you enjoyed reading the article and have an extensive overview of the pressure and fluid statics. Thanks for reading.



