Hello Friends. I hope you are doing great. In this article, I will cover the nature of flow responsible for the changes in density. The nature of flows responsible for density change is known as compressible flows.
Fluid dynamics and thermodynamics combine for the theory of compressible flows. The compressible flow creates a relationship with the ideal gas. First, I will explain the stagnation state, speed of sound, and then the Mach number. This all comes under compressible flows. Then there come the static and stagnation fluid properties, shock waves, and variation of fluid properties in the case of regular and oblique waves. All of these are discussed in this article. So without wasting any time, let us start with the Stagnation property.
Stagnation Property
The definition of the stagnation property is as follows:
The enthalpy and kinetic energy of the fluid is combined in a term called stagnation or total enthalpy.
The formula of Stagnation Property:
The procedure of stagnation property is as follows:
ho=h+V22
Units of Stagnation property:
The units of stagnation property are kilo Joule per kilogram.
Some of the essential key points related to the stagnation property are as follows:
In the definition of stagnation property, there is a term enthalpy. The enthalpy is the combined flow and internal energy of the fluid. The formula of enthalpy is given below:
h=u+P
It is better to say that enthalpy is equal to the total energy in the case when the potential and the kinetic energy of the fluid are not considered (or negligible).
So, when there are high fluid flows (usually in jet flows/high flows), the potential energy is not considered, whereas kinetic energy is thought. In this situation, the enthalpy and the kinetic energy combine and are called the stagnation enthalpy.
Whenever the fluid's potential energy is not considered, the total energy is said to be stagnation enthalpy.
To differentiate the stagnation enthalpy from the standard enthalpy, the ordinary enthalpy is known as static enthalpy. In contrast, both enthalpies become the same when the kinetic energy is not considered.
Derivation of Stagnation Enthalpy
I will share some essential points related to stagnation enthalpy in this part. So without wasting any time, let us start.
In order to start the derivation of the stagnation enthalpy, we will consider the preferably steady flow, which flows from a nozzle or diffuser. The main property of the flow is that it is flowing on its own, not with the aid of a motor or anything.
The same thing is also implemented; the potential energy is considered minor or negligible.
In this case of a single stream of the steady flow device, the energy balance equation is said to be as follows:
h1+V122=h2+V222 …(a)
h01=h02 (b)
It is better to say that the above equation represents that during the single stream steady flow, there is no change of potential energy, heat, and work interaction is also not present.
A decrease in static enthalpy is observed when there is an increase in velocity. This usually happens in devices that are diffusers and nozzles, respectively.
Another equation is observed, and from equation (a), the velocity of state two will equal zero when the fluid is stopped. So the equation transforms into new, and that is as below:
h1+V122=h2
h02=h1+V122
Another exciting fact says that when there is no heat transfer from the system to the system, it is called an adiabatic state. So the stagnation enthalpy is also considered to be the enthalpy of fluid.
Pressure and temperature also increase when there is the conversion of kinetic energy to enthalpy.
You might be wondering from the heading that says Stagnation Properties. So Stagnation Property is the property of fluid at the stagnation state.
You have observed from equation (b) that there is a transcript 0. So actually, 0 represents the stagnation stage.
Here is another term called isentropic stagnation state and the definition of it is as follows:
The isentropic stagnation state is the one when the stagnation process is adiabatic as well as reversible.
one of the salient features of the isentropic stagnation state is that the entropy remains constant, so in the case of an actual stagnation state, the entropy might increase or decrease depending on the situation.
Both the stagnation state and the isentropic stagnation state are considered the same sometimes.
There is another equation that says that in the case of an ideal gas, equation (b) will become as follows:
CpT0=CpT+V22
The final equation after dividing Cp from both sides is:
T0=T+V22Cp
Here T0 is said to be the stagnation temperature ( transcript with 0 presents stagnation state).
T0 is the temperature at which ideal gas adiabatically becomes a state of rest.
The next term is stagnation pressure. Before defining it, let us see the equation first, and it is as follows:
P0P=(T0T)k/(k-1) (c)
So stagnation pressure is defined as the pressure of a fluid that becomes in a rest state adiabatically.
equation (c) presents the stagnation pressure.
At the start of these critical points, I have used a term, i.e. single stream steady fluid flow. So for this term, the energy balance equation becomes:
qin+win+h01+gz1=qout+wout+(h02+gz2)
The equation in the case of an ideal gas with the specific heats will be as follows:
qin-qout+win-wout=CpT02-T01+g(z2-z1)
So here h02 and h01 are the stagnation enthalpies, whereas T02 and T01 are the stagnation temperature
So this is all from the stagnation enthalpy, property, temperature, and property.
Now I will explain what Mach number is and the speed of sound. So let us start.
Mach Number and Speed of Sound
Both are interrelated to, first, the speed of sound.
Speed of Sound
After reading the heading, you might be wondering why the article is about compressible flow low then why we are discussing the speed of sound. So better not to worry and let me explain to you in easy words.
The speed of sound in terms of compressible flows is explained as follows:
The sound rate is an integral part of the study of compressible flows as it is the sonic speed at which infinitesimally small pressure waves travel through a medium.
Some of the essential key points and the equation are discussed below. Have a look.
If you look into the definition, there is a statement that says that small pressure waves travel through some medium. Here the pressure waves are created from turbulence or some disturbance.
To explain the topic more precisely, I will explain the speed of sound through some theoretical derivation background.
There is a duct has fluid in it, and that fluid is at rest. There is also a piston inside the duct, which is moved inside. The piston is being moved at some velocity known as constant incremental velocity.
This disturbance of the piston moves the waves of fluid and the movement is made at the speed of sound.
The waves are separated from the fluid adjacent to the piston thus resulting in a change in thermodynamics property.
To elaborate on the whole scenario, the following diagram is presented below:
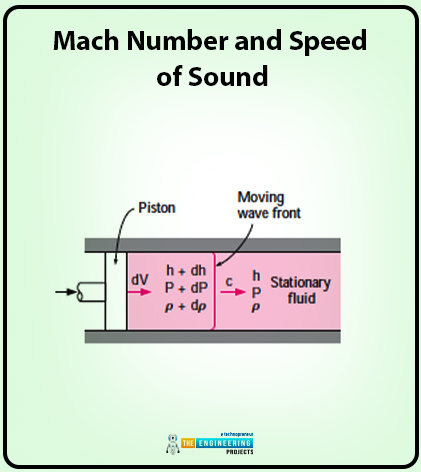
For a more precise explanation a control volume is considered., In this situation, the waves created by the disturbance or any movement inside remain within the boundary.
Here mass balance equation for the single stream, steady flow is as follows:
mright=mleft
And on simplification, the equation will become as follows:
ρAc=ρ+dρA(c-dV)
Let me explain this equation to you. As you know that in the above theory we have considered a control volume. So when something passes through, there are some movements of the waves, and the fluid moving in the right direction will now move in the direction of the wave front. The speed at which the fluid moves is the speed of sound c. Now the fluid moving in the direction of the left will move away from the wave front, and now rate will be c-Dv, respectively.
So I hope that now the equation is quite understandable to you.
we can further simplify the equation by deduction of cross-sectional area, and now the equation will become:
cdρ-ρdV=0 (a)
The definition of control volume says that there is no heat transfer and work done throughout the process. The equation will not have the potential energy for the steady flow process, and it will be as follows:
h+c22=h+dh+(c-dV)22 (1)
And after the simplification, the equation becomes as follows:
dh-cdV=0
You might be shocked at how the equation is reduced so much as it has so many terms before. So here is the answer. In equation (1), the term dV2 is not considered.
The ordinary sonic wave is nearly unneglectable. They are small, yet they are still considered. So they are somehow isentropic. Now the equation in the case of thermodynamics will be as follows:
Tds=dh-dP (b)
Here the term on the left Tds will be equal to zero, and after the simplification, the equation will become:
dh=dP (c)
For the calculation of the speed of sound, we will combine the equation (a), (b), and (c) will become as follows:
c2=dPdρ
After the simplification, the final equation for the speed of sound will be as follows:
c2=k(∂P∂ρ)T
So here is the final equation of the speed of the sound.
We are moving towards the second part, the Mach Number. Let us see the definition and the equations of it.
Mach Number
The Mach number is also one of the essential parts of compressible flows.
The definition of the Mach Number is as follows:
The Mach Number is the ratio of the actual velocity of the fluid to the speed of sound in the same fluid.
Formula of Mach Number:
The formula of the Mach number is as follows:
Ma=Vc
Some of the essential key points of the Mach number are as follows:
The Mach number has a direct relationship with the velocity of fluid means an increase in the Mach number increases the velocity and vice versa. Whereas the Mach number has an indirect relationship with the speed of sound. The increase in one quantity decreases the other.
There are some important parameters for the flow regimes, and they are as follows:
In the case of
Sonic Mac=1
Subsonic … Mac<1
Supersonic Mac>1
Hypersonic Mac≫1
Transonic Mac≅1
One-Dimensional Isentropic Flow
While discussing the flow type, the one-dimensional isentropic flow comes under the compressed fluids.
Examples:
The nozzle diffusers and the turbines are examples of one-dimensional fluid flow.
Some of the essential key points related to the one-dimensional isentropic flow are as follows:
I will explain to you the theoretical background of the one-dimensional flow. Before that, look at the diagram as it will be convenient for you to understand the theory.

As you have seen the diagram and know about the number, let me explain. The value of the Mach number is one at the smallest flow area, called the throat.
Increase in fluid velocity is observed when the fluid passes through the throat. But this increase in velocity is also due to the decrease in the density of the fluid.
If you have a look at the diagram, then there is a word i.e. converging nozzle. But here the converging-diverging nozzle is used so it is the one in which the flow area first increases and then decreases at the throat. Some might confuse these converging nozzles with the Venturi ones. But the Venturi nozzles are used for the incompressible flow.
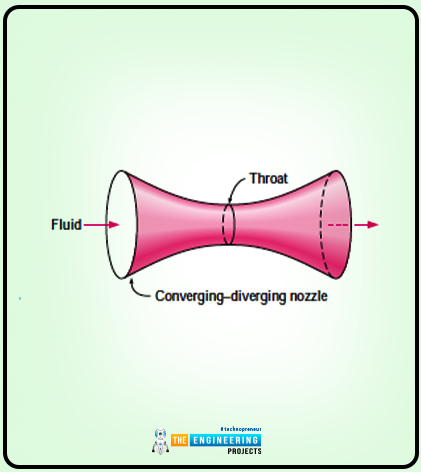
Variation in Fluid Velocity with Flow Area
In this topic, we will pinpoint the main parameter that involves the coupling in the case of isentropic duct flow between the density and velocity.
In this area, we will look forward to some equations of steady flow and the changes in the fluid velocity accordingly to the flow area. So following are some essential key points related to it:
The equation will present the relation between the temperature, pressure, density velocity, Mach number and flow area. These are the equation for the isentropic one-dimensional flow.
The following is the mass balance equation in the case of a steady flow process:
m=ρAV=constant (a)
The equation (a) will be differentiated and divided and the following result will be obtained;
dρ+dAA+dVV=0 (b)
Now the next equation will be related to the isentropic flow in which there is no potential energy and it is as follows:
dP+VdV (c)
The next equation is expressed in terms of Bernoulli’s Equation and again the potential energy is neglected. For convenience, we will combine the equation (b) and (c) and it will become:
dAA=dP(1V2-dρdP)
Now here comes the final equation that describes the isentropic flow in the terms of changes in the pressure accordingly to the flow area.
dAA=dPV2(1-Ma2)
The above-mentioned equation has everything it has an area, density, pressure and Mach number
For this equation there are some limitations in the case of Mach number and they are mentioned below:
Subsonic Flow … Ma<1 and (1-Ma2)term is Positive
Supersonic Flow Ma>1 and (1-Ma2) term is negative
Let me explain these limitations more extensively. In the case of subsonic, the value of differential is dA and differential pressure dP should have the same signs. The increase in pressure increases the flow area and vice versa. Meanwhile, in the case of a supersonic, the value of a differential area and the pressure should have opposite signs. Also, an, increase in pressure quantity should have decreased the flow area of the duct.
There is another equation that is also related to the isentropic flow and it says in equation (c) the value of density and value is substituted in the final equation and it is as follows:
dAA=dVV1-Ma2
So ending this topic on the limitations of Mach number for this equation and they are as follows:
Subsonic Flow (Ma<1) dAdV<0
Supersonic Flow (Ma>1) dAdV>0
Sonic Flow (Ma=1) dAdV=0
Isentropic Flows for Ideal Gas
While discussing the isentropic flow this topic holds its importance as related to the ideal gas. Let’s have a look at the equations and some important key points of it:
For ideal gases both the static and the stagnation properties are combined together, and with the help of the Mach number and specific heat, the equations will be transformed.
The first equation is about the stagnation temperature T0and the ideal gas temperature T. And the equation will be like this:
T0=T+V22Cp
And after simplification, the equation will become:
T0T=1+V22CpT
In this equation, we will substitute the values of V and specific heat. The values we will be substituting are:
Cp=kRk-1
c2=kRT
Ma=Vc
After substation of all the values and doing the simplification, the final equation will become:
T0T=1+(k-12) Ma2
If you remember that at the start, I used two terms, i.e., static and stagnation pressure. So now, I will show you one by one equation of both these terms, and they come under ideal gas. So presenting you the ratio of stagnation to the static pressure, and the equation is:
P0P=[1+k-12Ma2]kk-1
This equation is the result of substituting the value of T0T in this equation.
P0P=(T0T)k/(k-1)
Now presenting you the ratio of stagnation to static density:
0=[1+k-12Ma2]kk-1
There is some limitation where the value of the Mach number is one, so all the points where the Mach number is unity are called the Critical Properties.
While writing the equations of compressible flows the asterisk( *) is used to present the critical points. So their equations will be as follows:
T*T0=2k+1
P*P0=(2k+1)k/(k-1)
*0=(2k+1)1/(k-1)
So these are the equations that present the critical points. That is all from the one-dimensional isentropic flow.
Isentropic Flow through the Nozzle
In compressible flows, isentropic is considered to be one of the most important branches of it. Here under this topic, I will discuss the isentropic flow that passes through the nozzles, what are their nature equations, and the nozzle type. Let us start.
First of all, I will share some of the essential key points with you that covers all the information about the topic.
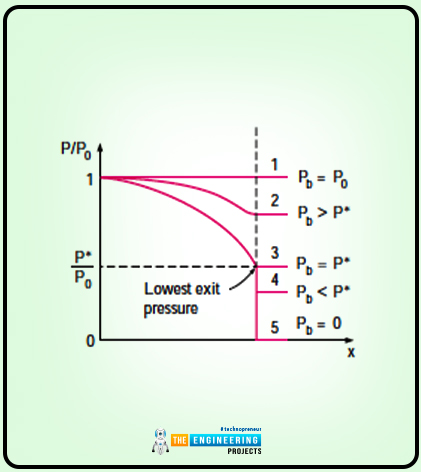
Here in this topic we will learn a new term i.e. Back pressure. A brief definition of back pressure is as follows:
Back pressure is pressure that is applied at the discharge region of the nozzle.
Here the nozzle can be converging and diverge depending on its requirement of it. I will discuss the nozzle type and the isentropic flow through it.
Converging Nozzle
The derivation and the equation of the converging nozzle are as follows:
A subsonic flow is considered in the case of a converging nozzle. The diagram elaborates on the flow:
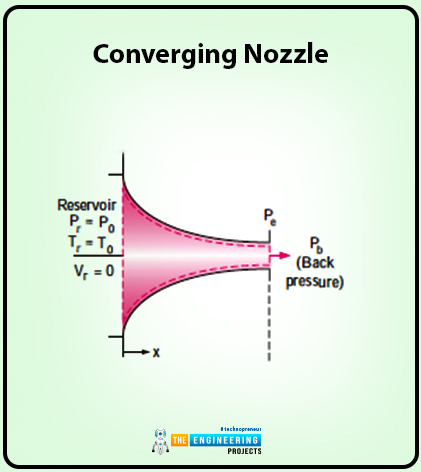
Here you can clearly see that the inlet of the nozzle is connected to the reservoir. The temperature is presented as Tr whereas the pressure is as Pr respectively.
the velocity at the inlet is neglected and the flow is isentropic. The reservoir has a huge volume so that is the main reason the fluid velocity’s not being considered.
The reservoir pressure and temperature are equal to the nozzle’s pressure and temperature.
Now the working is being followed and the back pressure is being reduced. After doing so the change in the flow pressure is observed.
The back pressure is equal to the P1 and that P1 is equal to the reservoir pressure. This is all due to the uniform distribution of pressure among the nozzle.
Similarly when the back pressure is reduced to P2 then the value of at the outlet becomes equal to P2 also. As a result of this procedure, the pressure of the nozzle decreases in the direction of the flow.
This all working is elaborated by the diagram mentioned below;

The back pressure is now reduced at pressure point three and that is equal to the critical pressure. Actually, pressure three equal to the critical pressure shows that the pressure that is required by the fluid increases the velocity of the fluid and this increases the speed of sound at the throat.
Now the back pressure is reduced to pressure point four. Here there is no change in the pressure and the flow is being observed as it is at the end position.
Now we will look forward to the equation that is related to the mass flow rate.
m=ρAV
m=PRTAMakRT
m=PAMakRT
We will do further simplification and the final result will be as follows:
m=AMaP0k(RT0)[1+(k-1)Ma2/2](k+1)/[2k-1]
Whenever there is a Mach number there are certain limitations as discussed above according to the equations. Here when there is a specified flow area the mass flow rate can be determined by differentiating the above equation and equalizing it to zero. The value of the Mach number here is one. We all the when the value of the Mach number is one (it is at the throat) and the mass flow is maximum at the throat.
Now the equation will be as follows:
m=A*P0kRT0(2k+1)(k+1)/[2k-1]
In order to have a maximum flow rate there are two parameters to be fulfilled. The temperature and the pressure at the inlet of stagnation of a given throat give the maximum flow rate in the case of an ideal gas.
It is a characteristic property that by changing the stagnation pressure and temperature we can control the flow rate values.
So these are the theoretical background and equation related to flow rate. Hence there is another point related to this topic and that is the critical Mach number.
The equation for it is the same as the formula for the Mach number but there are a few modifications, and they are as follows:
Ma*=Vc*
The formula can be expressed in the term of temperature, and the working is as follows:
Ma*=Vc.cc*
Ma*=Ma. cc*
Ma*=MakRTRkT*
Ma*=MaTT*
We can further simplify this equation and can get the final critical Mach number equation so by substituting the values of local and critical temperature, we get:
Ma*=Mak+12+(k-1)Ma2
So, this is the final equation. There is a difference in both the values of the Mach number.
The critical Mach number Ma* is the local velocity non-dimensionalized concerning the sonic velocity at the throat. The other one Ma is the local velocity non-dimensionalized concerning the local sonic velocity.
Their values also differ from one another. The value of Ma* is provided on a table that is listed against the Ma when the value of k is 1.4.
The table is shown below for your clarification:
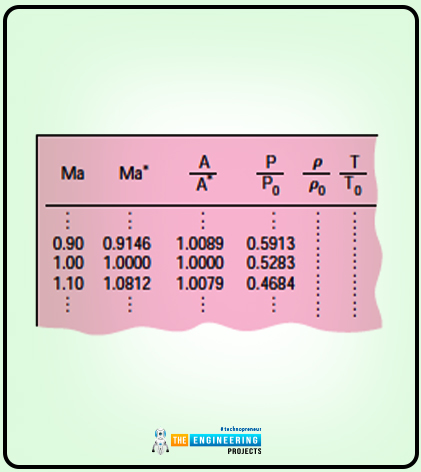
So that is all from the isentropic flow through nozzles. Let’s move toward the next topic, related to the waves.
Shock Waves and Expansion Waves
Where ever there is flow, there are waves created. As we have studied in depth how sound waves are made, the question is how shock waves are formed. Let us have a concept about it.
How are shock waves created?
There are changes in the fluid properties that can either be temperature pressure, increase or decrease in volume, etc. These changes occur in a thin layer of the converging-diverging nozzle under supersonic flow conditions. So in this way, shock waves are created. Now I will explain the type of shock waves, their working principle, and the equations. So without wasting any time, have a look at it.
Normal Shock Wave
The definition of normal shock waves is as follows:
The normal shock waves are the ones that form in a plane normal to the direction of flow.
Some of the essential key points, along with the equations of normal shock waves, are explained below:
The shock wave is all irreversible and not being approximated as being isentropic.
The process includes all the energy, momentum, and conservation of mass relation to define the flow properties before and after shock.
The normal waves are different in the sense that they are thin and this property benefits the entrance and exit flow areas. The exit and the entrance flow area are the same.
Now moving towards the mathematical part. Let’s start with the conservation of mass. As you all know about the formula of conservation of mass but for convenience let me show you.
1AV1=2AV2
The equation can further be simplified with the cancellation of cross-sectional area.
For the conservation of energy, the equation is as follows:
h1+V122=h2+V222
Now let’s have an overview of the conservation of momentum:
AP1-P2=m(V2-V1)
While working on the equation for the normal shock waves we combine the law of conservation of mass and energy into one equation.
The equation is then plotted on the h-s diagram.
If you look at the diagram below, it shows all the important aspects that I am going to share.
The h-s diagram shows a line i.e., Fanno Line and that is the resultant curve. This curve has similar values of stagnation enthalpy and mass flux.
Moving towards the second curve i.e. the Rayleigh Line. There are two point on the h-s diagram and these two points are correspondence to the Mach (Ma=1).
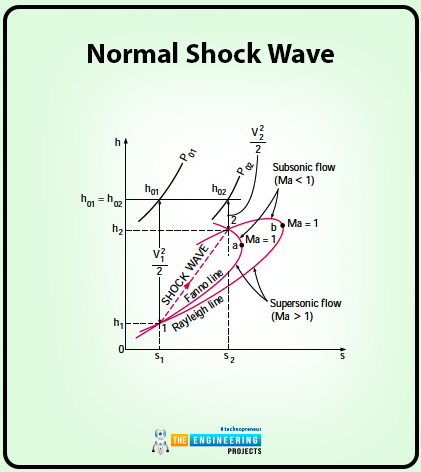
Further you can see in the diagram that the upper part is for the subsonic flow whereas the lower part is for the supersonic flow.
The two lines Fanno and the Rayleigh line intersect at two points as you can see from the diagram. One point presents the condition that is before the shock and the second shows after the shock condition. At point 1, it is supersonic and before shock condition, whereas at point 2 it is subsonic and aftershock condition.
Also the high is the value of the Mach number before the shock there is a chance that the shock will occur.
When the Mach number is unity then the shock waves are simply sound waves.
One of the important points related to this is that the conservation of energy principle demands that the stagnation enthalpy should be constant throughout the process.
h01=h02
In the case of an ideal gas, the enthalpy is as follows:
T01=T02
After the shock, the temperature of the ideal gas remains constant.
Moving forward, there are some important equations that are related to the ideal gas. These equations show the before and after shock and after substituting the values required results can be obtained.
So following are two important equations.
T01T1=1+(k-12)Ma12
T02T2=1+(k-12)Ma22
We will further simplify the equation by taking T01=T02 and the result will be:
T2T1=1+Ma12(k-1)/21+Ma22(k-1)/2 (a)
In the case of an ideal gas, we know that:
1=P1RT1
2=P2RT2
The value of temperature can be easily substituted using the law of conservation of mass while the values of Mach number and c are used which we can substitute in equation(a). the values are as follows:
Ma= V/c
c=kRT
Now we can substitute all the values and get the result as follows:
T2T1=P2V2P1V1=P2Ma2c2P1Ma1c1=P2Ma2T2P1Ma1T1=(P2P1)2(Ma2Ma1)2 (b)
Now this is the final result we get after substituting all the values. We can further simplify this equation and can get the equation for the pressure ratio across the block and for that we will combine the equation (a) and (b):
P2P1=Ma11+Ma12(k-1)/2Ma21+Ma22(k-1)/2
If you recall the law of conservation of mass and energy, then after looking at the equation you will understand that it is the combination of laws.
Thus this equation about the Fanno Line for ideal gas.
The other curve is Rayleigh Line and its derivation is as follows:
P1-P2=mAV2-V1
P1-P2=2V22-1V12
As:
V2=(PRT)(Ma.c)2
V2=(PRT)(MakRT)2
V2=Pk Ma2
The pressure ratio can be as follows:
P2P1=1+kMa121+kMa22
Now we will move towards the final equation that is about the Fanno and the Rayleigh lines relating the Mach number upstream of a shock to that downstream of the shock. Let’s us have a look at an equation:
Ma22=Ma12+2/(k-1)2Ma12k/(k-1)
Oblique Shock
The oblique shock is a type of shock waves. It is better to say that there are various variations of waves. So moving toward the topic in order to define the oblique shock I will explain it through an example. So have a look at the example:
Example:
The space shuttle traveling through the atmosphere at supersonic speed creates a complicated pattern with shock waves. Such complex patterns and shock waves are called Oblique Shock Waves.
The following is the diagram that elaborates the shock waves:
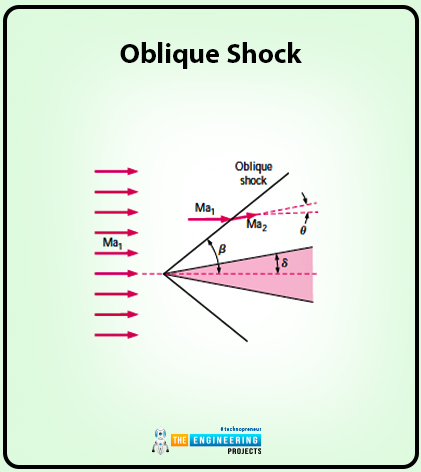
Some of the essential key point and equations related to the oblique shock waves is as follows. Have a look at it:
Here in the diagram you can see there are some certain angles mentioned and they these angles helps in the formation of the oblique shock waves.
So talking about the first angle i.e. the theta and this is named as a turning angle or angle of deflection. The background of this angle is that at first, we consider the oblique shock waves traveling in a straight line. This straight line is much similar when the Ma>1 and in supersonic flow, a two-dimensional wedge half angle is formed. So here the fluid cannot flow through the wedge and at that point, it turns into the turning angle.
The other angle is about the shock angle or wave angle (). The background of this angle is that when the turning angle is formed then the straight oblique shock wave is formed and this wave is aligned with the wave angle.
For the conservation of mass, the wave angle should be greater than the two-dimensional half-wedge angle.
In the case of supersonic flows, Reynold’s number has a high value, and the boundary layer along the wedge is thin so its effects are not considered.
Now the flow is turned by another angle that is much similar to the wedge angle and it is named a deflection angle .
The deflection angle is the same as the half wedge angle.
Here there is an interesting fact about the half wedge and deflection angle i.e. when the thickness effect of the boundary layer is considered then the deflection angle is observed to be greater than the half wedge angle.
In the case of the oblique shock waves there are also the limitations of the Mach number. A decrease in the Mach number is observed in oblique shock waves.
Also oblique shock waves are possible when the upstream flow is supersonic.
Now moving towards some mathematical part of the oblique shock waves. The straight oblique shock wave is considered.
The diagram below shows the straight oblique shock waves:
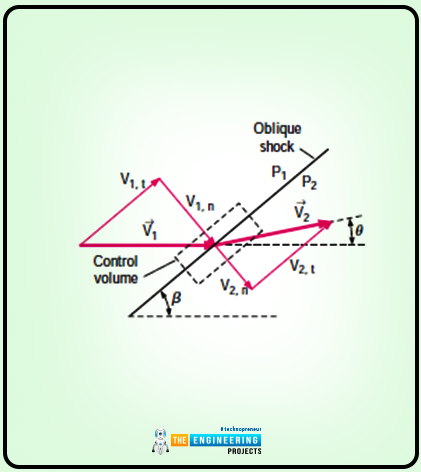
Now here you can see that the straight wave is decamped into the velocity vector upstream and downstream of the normal and tangent components.
For working a small control volume is being considered and all the working happens on it.
If you look at the diagram closely, the upstream of the shock, all the fluid properties (such as pressure velocity) along the lower left face of the control volume are similar to those of the upper right face.
In this case, the law of conservation of mass equation is changed into the following equation:
1V1,nA=2V2,nA
Canceling the area of the control surface (A) on both sides we will get:
1V1,n=2V2,n
There is another important point related to the tangential component of velocity. So the tangential component of the velocity is parallel to the oblique shock and in order to prove this point the tangential momentum equation to the control volume is applied.
So conservation of momentum is being applied in the normal direction to oblique shock waves. So the equation we get is as follows that presented the forces that are only pressure forces:
P1A-P2A=ρV2,nAV2,n-ρV1,nAV1,n
P1-P2=2V2,n2-1V1,n2
Since we have considered a small control volume so we know that there is no transfer of heat and no transfer of work done. The stagnation enthalpy also does not change and eventually, the conservation of energy equation becomes as follows:
h01=h02=h0
h1+12V1,n2+12V1,t2
h2+12V2,n2+12V2,t2
Here the V1,t=V2,t. The equation will be reduced as follows:
h1+12V1,n2=h2+12V2,n2
Here is the final equation.
You might have observed that the equation of the conservation of mass, energy, and momentum have the same equations but when we are writing them in the terms of normal velocity components then they vary. But the equation for the normal shock is the same.
The equations that are derived for the normal shock waves can be applied oblique shock waves. Here is a condition that the oblique waves equation should be written in the terms of Mach number.
So we come to the conclusion that the equation for the oblique shock waves is much similar to the normal ones but the only difference is that the normal components of the Mach number are used in oblique ones.
Prandtl-Meyer Expansion Waves
It is also one of the important types of waves and it may differ from other ones also. Let us share some of the important key points related to it;
One of the important points about the supersonic flow is that when it travels in the opposite direction just in the upper portion of a two-dimensional wedge at an angled attack is greater than the half-angle sigma (δ).
The flow of such kind is known as expanding flow. But when the flow is in oblique shock then the flow is called the compressing flow.
The diagram shows the whole flow type and the angles created by it.
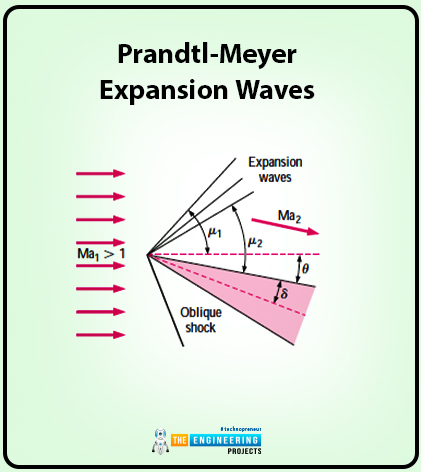
So there is not a abrupt change in the turning of flow by the shock but the Mach wave turn and thus the flow also turn by infinitesimal amount.
One of the important information about the flow is that the flow is isentropic.
In the downstream direction, a decrease in the pressure, temperature and density is observed whereas the Mach number increases.
Just have a look at the diagram you will see that Prandtl-Meyer is inclined at some angle called the Mach angle (μ) also the first expansion wave has an angle and we call it Mach angle. This angle is determined in the following way:
1=(1Ma1)
2=(1Ma2)
Now there is important to question how can we determine the Mach number 2. So for Ma2, there is a formula for it and that formula shows a turning angle across the expansion fan and can easily be calculated by integration. So the formula is as follows:
=v(Ma2)-v(Ma1)
Now, this is the formula for the turning angle across the expansion fan and can be used to find Ma2.
Here in this formula vMa is the Prandtl-Meyer function and it has an equation where we can find the unknown. So the equation is as follows:
vMa=k+1k-1( k-1k+1(Ma2-1))-( Ma2-1)
Here is an important point and i.e. that vMais an angle and it should not be confused with kinematic viscosity.
When the Mach number is unity then the Prandtl-Meyer function vMa taken as zero for getting the supersonic Mach number (Ma>1)
One of the interesting features of the Prandtl-Meyer function is that it has numerous advantages in our daily life.
Applications (Shock wave/Boundary-Layer)
The shock wave and boundary layer both have a unique significance. There are numerous advantages of both of these in our daily life.
The following are some important applications of shock waves and boundary layers. Have a look at them:
The boundary layer is susceptible to separation from aerodynamics whenever strong adverse pressure occurs
The shock wave on the other hand produces a strong pressure gradient.
Whenever the boundary layer and the shock wave interact with each other the result is a complex flow pattern and in some cases, the boundary layer separates from the region on which it is attached
The interaction between the shock wave and the boundary layer is viscous and inviscid interaction in which the viscous flow in the boundary layer encounters the essentially inviscid shock wave that is generated in the free stream.
The change in the shock wave and the boundary layer continues until an equilibrium condition is reached.
The shock wave and boundary layer have become one of the most pacing problems of modern fluid mechanics research.
Conclusion
Dear friends I hope you have enjoyed reading the article. I have tried best to explain extensively about the compressible flows, isentropic flows, shock waves, boundary layers, and the applications of both of them. That’s all my side. Thanks for reading.



