Before starting this important topic there are some of the important terminologies related to the theorem that are frequently used throughout. So let us have a look at them.
System
Some important key points related to the system are as follows:
In thermodynamics, a system is a quantity of matter of fixed quantity.
The system is mostly closed. system. There is a change in the size and shape of the system but due to the closed system, no mass can cross the boundary.
One of the important points is that the mass of the system remains constant.
Control Volume
Some important key points related to the control volume are as follows:
The control volume is also known as the open system and it is defined as the region that is specified for a case study.
In the case of a control, volume mass can cross and move in and out of the boundary and which is called the control surface.
One of the important key points related to the control volume is that the mass of the control volume decreases during the process but, the volume remains constant.
Reynold’s Transport Theorem
The important key points related to Reynold’s Transport Theorem are as follows:
In fluid mechanics, control volumes are easy to handle and many of the laws and theorem are based on it.
So Reynold’s Transport theorem is actually a relationship between the rate of change of extensive properties of the system and control volumes.
A system is considered arbitrary when Reynold’s Theorem is being considered. But here the derivation is also being carried away.
Reynold’s Transport Theorem provides a relationship between the system and control volume.
Derivation of Reynold’s Transport Theorem
Let us start the theorem with a background of it:
First of all, we will consider the flow that is moving from left to right and that flow is passing through an expanding field.
As the fluid flow the upper and the lower bounds of the fluid flow are considered to be streamlines of flow. Between any two streamlines, it is assumed automatically that the flow will be uniform and so in this situation, it is also considered.
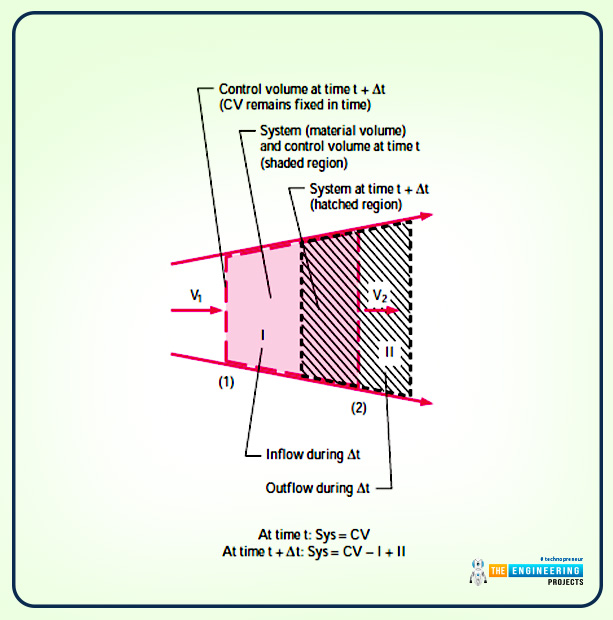
So there is a diagram that is mentioned below that shows the moving system and control volume (shaded region) of the flow field is considered at the times t and ∆t. the streamlines are also shown.

Here one interesting fact is that the system and the control volume are the same as the system seems to be coinciding with the control volume.
With reference to the diagram, in part (1) the system moves with uniform speed V1 and so in part (2) it moves with speed V2 uniformly.
If you look at the diagram, then there is a central region called the hatched region.
The region that is uncovered by the system during the motion is mentioned as section I and this is part of the control volume. but the new region that is covered by the system is said to be section II and this is not part of the control volume.
Now let us start the derivation. For derivation let us suppose B as extensive property and that may be mass, energy or momentum.
Moreover, let us suppose
b= B/m
Now this b=B/m is the intensive property (we are supposing it).
So the extensive property is additive, they can be added easily.
so the extensive property at times t and ∆t are presented as follows:
Bsys,t=BCV,t
Bsys,t+∆t=BCV,t+∆t - BI,t+∆t+BII,t+∆t
Now we will get to the final result by taking two steps. The first step will be subtracting equation 1 with equation 2 and then taking the limit ∆t→ 0. So the final result will be:
dBsysdt=dBCVdt-Bin+Bout
The value Bin and Bout is as follows:
Bin= b11V1A1
Bout= b22V2A2
Here A1 and A2 are the cross-sectional areas.
And the values of BI, t+∆t and BII, t+∆t is as follows:
BI, t+∆t = b11V1∆tA1
BII, t+∆t=b22V2∆tA2
Now we are on the second last step and it is as follows:
Bin=BI=b11V1A1( after taking limit)
Bout=BII=b22V2A2 (after taking the limit)
The important point here is that property is the extensive property and the time rate change of the system is equal to the time rate of change of B of control volume along with the net flux B of control volume by mass.
Now the final result will be:
Bnet=Bout-Bin=∫CS ρbV.n dA (inflow is negative)
So below mentioned is the diagram that shows the whole working of the derivation:

In the case of the control volume, the equation will be as follows
BCV=∫CV ρb dV
Here the following equation presents the time rate of change of property B content of the control volume:
dBCVdt= d/dt∫CV ρb dV
so the system to control volume in the case of the fixed control system will be as follows:
dBCVdt= ddt∫CV ρb dV +∫CS ρbV.n dA
So that is the explanation related to Reynold’s Transport Theorem.
Conclusion:
I hope you have learned a lot through this article. Thank you for reading.



