The article will cover essential aspects of fluid statics and pressure forces applied to the fluid. The article will start with the absolute pressure gauge and the variation of pressure with depth in different gravitational field manometers and barometers, respectively. Then I will explain the forces that deal with fluids, such as hydrostatic force, buoyant force, etc. So, dear friends, without wasting any time, let’s start.
Pressure
The definition of pressure according to fluid mechanics is as follows:
Pressure is the normal force applied by a fluid per unit area.
Unit of Pressure
The units of pressure Pascal is too small to deal with in practical cases. For instance,
Kilopascal: 1kPa=103Pa
Mega Pascal: 1MPa=106Pa
The three common pressure units used are standard atmosphere bar and kilogram-force per square centimeter.
1bar=105Pa=0.1MPa=100kPa
1atm=101,325Pa=101.325kPa=101325 bars
1 kgf/cm2=9.807 N/ cm2=9.807×m2=9.807×104Pa
=0.9807bar
=0.9679 atm
The unit of pressure in the English system is pound-force per square inch (psi or lbf/in2)
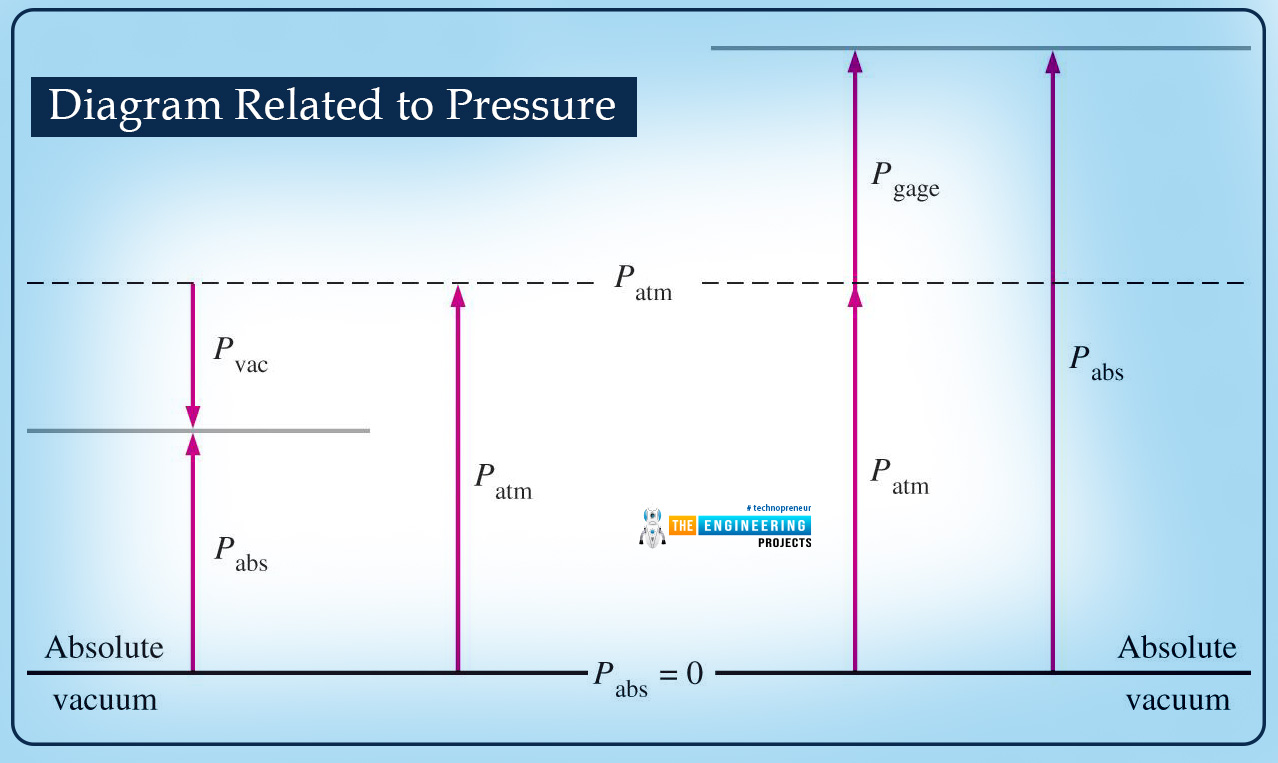
Absolute and Gage Pressure
The actual pressure at a given position is called absolute pressure. The pressure is measured relative to an absolute vacuum or absolute zero pressure.
The difference between the absolute and local atmospheric pressure is called gage pressure.
The pressure below the atmospheric pressure is called vacuum pressure.
Formula of Gage, Absolute, and Vacuum Pressure
All three of these pressures are interrelated with each. Other, and this is visible with the formulae as mentioned below:
Pvac=Patm-Pabs
Pgage=Patm-Pabs
Diagram Related to Pressure
The following diagram shows the relation of the pressures from the below-mentioned diagram:
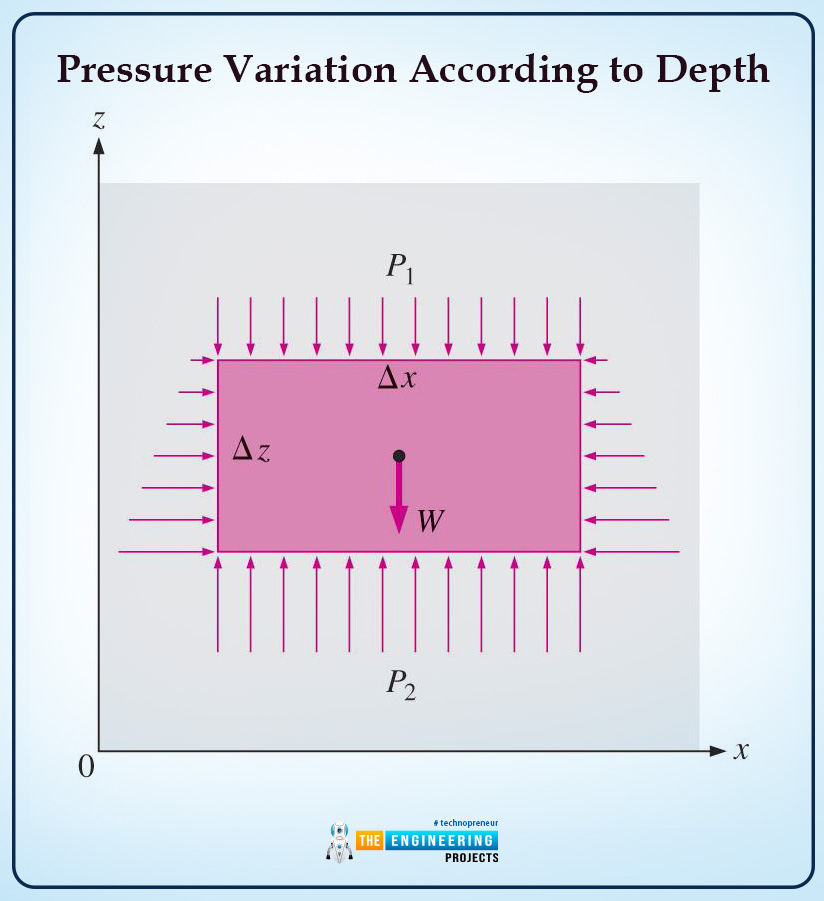
Pressure Variation according to Depth
We all know there is no fluid pressure change at rest and in the horizontal position. This phenomenon can further be elaborate on a few points:
Assuming a thin layer horizontally of fluid followed by force balance at any point. The pressure increases as the depth increase as there are more layers of fluids, and these layers are being balanced by the pressure increasing.
An example can explain the whole phenomenon.
Toto show how pressure changes with the change in depth. We assumed a rectangular fluid element, as shown in the diagram.
The length, width, and heights are mentioned on the diagram.
The pressure of the fluid is constant, whereas force balance in z direction vertically will be:
∑Fz=maz=0
P2△x-P1△x-ρg△x△z=0
Now, we will divide the above equation with delta x △xand will get the below-mentioned equation:
△P=P2-P1=ρg△z=sz
Here, one of the most important things is that the s is the specific weight of fluid.
The final statement to be noted is that there is an increase in pressure linearly with an increase in depth.
It is essential to note that the pressure force applied by the fluid is always normal at some points to the surface.
Pressure at Point
As pressure is a scalar quantity, sometimes it seems to be vector one. The pressure will be the same in any fluid at any point. To prove this point, let us discuss a scenario.
Let us consider fluid element (a wedge shape/ right-angled triangle) at equilibrium.
The mean pressures at three surfaces are mentioned as P1, P2, and P3, respectively.
The diagram shows the points clearly.

Here, the value along the pressure is the surface area.
According to Newton’s second law, the force in the direction of x and z is as follows as △y=1:
∑Fx=max=0 P1△z-P3Isinθ = 0 (1)
∑Fz=maz=0 P2△x-P3Icosθ-12ρg△x△z = 0 (2)
Here, the value of w is the weight of the fluid, and the value is as follows:
W=mg
W=ρg△x△z/2
The value of △x and △z are as follows:
x = I cos θ
△z=I sinθ
So, by substituting all the values in equations 1 and 2 and then diving equation 1 with △z and equation 2 with △x then, the final result will be:
P1-P3= 0 (3)
P2-P3-12ρg△z=0 (4)
Here, in equation 3 △, z drops to 0, and the final result will be:
P1=P2=P3=P
Pressure measuring devices
Numerous devices are used to measure fluid pressure and work on different principles. These devices are explained below briefly.
Manometer
The definition of a manometer is explained as follows:
A manometer is a device in which fluid columns measure pressure differences.
The important key points about the manometer are explained below:
the manometer is used to measure small or moderate pressure differences.
If pressure is at a specific position inside any gas tank, then the pressure anywhere in the tank will be the same. But here important point to be noted is that it is for gases only as their gravitational effect is negligible.
The basic diagram of the manometer is shown as follows:
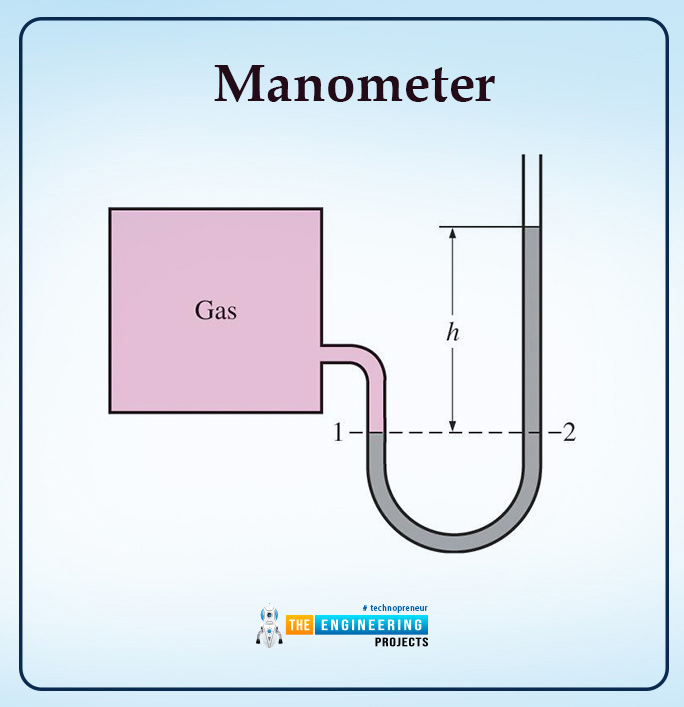
As we can see, two points in a basic barometer and a height h. So the pressure at point 1 will be the same throughout the tank so that P1=P2 and the pressure will be by the equation:
P2=Patm+ρgh
Here, h is the height of column fluid, which is in static equilibrium, and as we can see, the column is exposed to the atmosphere.
is the density of the fluid, and Patm is the atmospheric pressure.
Here, one important point to be noted is that the height of the tube is independent of the area of the tube.
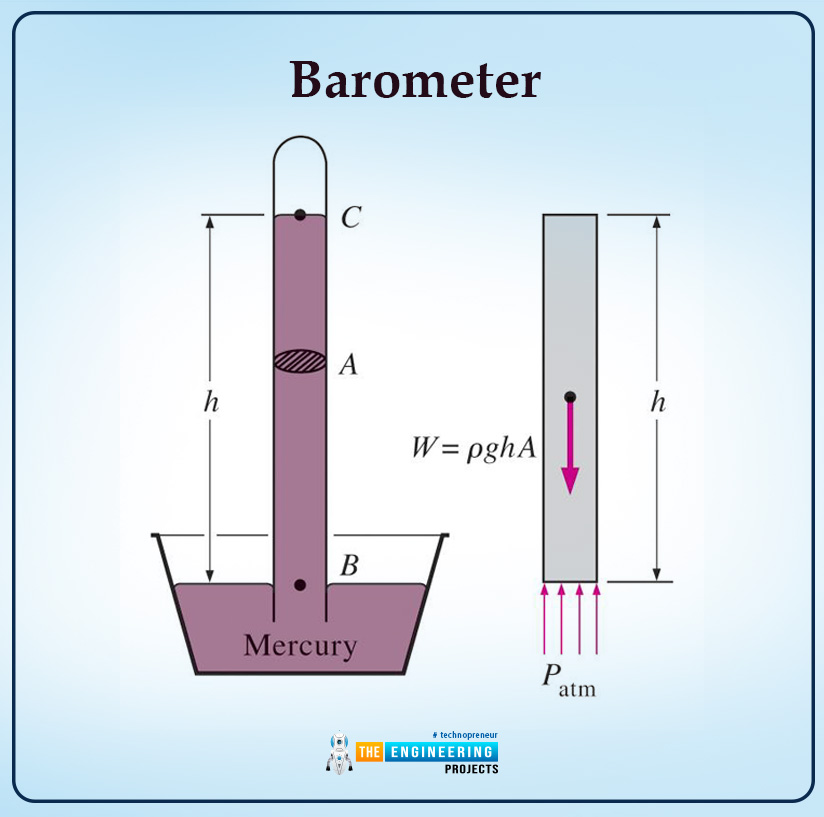
Barometer
The definition of the barometer is as follows:
A barometer is a device that is used for the measurement of atmospheric pressure.
The following are some important key points related to the barometer:
The structure of the barometer is the inversion of a tube filled with mercury in a container, which is exposed to the atmosphere.
The diagram shows the structure of the barometer;

Toto calculates the formula of the atmospheric pressure; we will follow the above diagram. As you can see, there is a point B, so this B equals atmospheric pressure. Point C inside the tube is assumed to have zero pressure as there are only mercury vapors above point C, and pressure above that point is low compared to the atmospheric pressure, so for ease, the pressure is taken to be zero. The formula of pressure is as follows:
Patm=ρgh
Other Pressure Measuring Devices
There are many other pressure-measuring devices that are in use in our daily life, and they are briefly explained as follows:
Bourdon Tube is a pressure measuring device consisting of a hook like a hollow metal tube that is connected to a dial indicator. There is a fluid inside the tube that is pressurized. When this fluid is being pressurized up to a point then the needle that is on the dial is deflected. The needle is read to zero when the tube is exposed to the atmosphere.

There are special types of pressure detectors that can convert the pressure effect into electrical energy and they are called pressure transducers.
When the mechanical pressure is created when the electric potential is applied to a crystalline form. Such kinds of devices are called Piezoelectric transducers.