The statement of Bernoulli’s Equation is as follows:
In fluid dynamics, Bernoulli’s Equation states about an increase in speed of fluid that occur simultaneously with the decrease in static pressure or decrease in fluid’s potential energy.
After reading the statement, you might have little idea what Bernoulli’s equation is about. Don’t worry. Here I am to explain that to you extensively.
Some of the important critical points related to Bernoulli’s equation are as follows:
Bernoulli’s equation is the relation between the pressure, velocity and potential energy.
This equation is only applicable for steady, incompressible flows. In this equation, all the frictional effects are neglected.
We will derive Bernoulli’s equation with the help of the Conservation of Linear Momentum Principle.
There are certain restrictions in the application of Bernoulli’s Equation. For instance, we cannot apply the equation to every fluid. Obviously, there should be a certain amount of viscosity in the fluid (some fluid has less value of viscosity) and the equation cannot be implemented in every flow.
So we conclude our statement by saying that Bernoulli’s equation is only applicable to inviscid regions of the flow.
So following is the diagram that shows the regions where Bernoulli’s Equation is applicable and where it is not.
The Bernoulli’s Equation id helpful in regions outside the boundary layers where the fluid motion is governed by the combined effect of gravitational and pressure forces.
The path and motion of the particle are described by the velocity vector. In the case of steady flow, the particle passes through streamlines.
Acceleration of Fluid Particle
The acceleration of the fluid particle is one of the most important topics while describing Bernoulli’s equation. So following are some important key points related to the acceleration of fluid particles:
While describing the motion and path of fluid particles, it is important to describe the distance along the streamline with the radius of curvature of the streamline.
Obviously when we are explaining the distance of a fluid particle then velocity can also be related to it. But here is a condition the velocity may vary along the streamline.
In the case of defining the acceleration of fluid particles of two-dimensional flow, the acceleration is divided into two parts. One is the normal acceleration an and one is the streamwise acceleration as respectively.
The normal acceleration is due to the change in direction whereas the streamwise acceleration is due to the change in speed.
There is a condition that when the particles are moving in a straight path the normal acceleration is zero since there is no change in direction and the particle is moving in a straight line so the radius of curvature is infinity.
Bernoulli’s Equation is the result of force balance along the streamline.
We might wonder that in steady flow the acceleration is zero. But here is an interesting fact the acceleration is not zero. We define acceleration as the rate of change of velocity in time but there is no change in time. In order to exemplify this point garden hose is one of the perfect examples to describe. There is a steady flow in the garden hose and steady means no change with time but the quantity may change. When the water accelerates along the nozzle then there is a change in velocity at the inlet and outlet but at a specific point it remains constant.
So mathematically representation of velocity is as follows:
dV= ∂V∂sds+∂V∂tdt and dVdt=∂V∂sdsdt+∂V∂t
In the case of steady flow,
∂V∂t=0
And
V=V(s)
The equation of acceleration will be as follows:
as=dVdt
as=∂V∂sdsdt
as=∂V∂sV
as=VdVds
Derivation of Bernoulli’s Equation
Before starting the derivation of Bernoulli’s Equation let us overview the statement of Bernoulli’s Equation and that is as follows:
The sum of kinetic, potential and flow energies of a fluid particle is constant along the streamline during the steady flow neglecting the frictional and compressibility effects.
Let us start the derivation of Bernoulli’s Equation with the theoretical part:
First of all, consider the fluid particle in a flow field with steady flow. The fluid particle is shown in the diagram as follows:
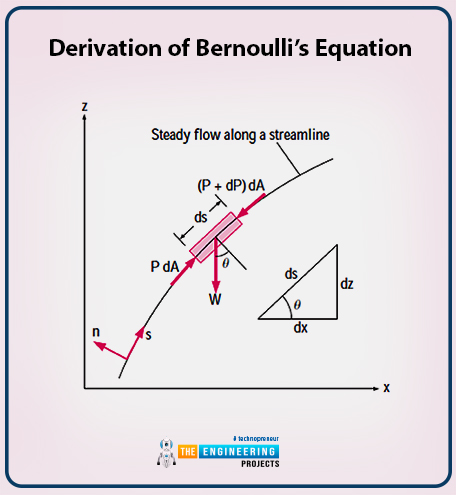
According to Newton’s Law states as
The conservation of linear momentum relation in fluid mechanics.
The fluid particle moving in the s direction along the streamlines gives the following force according to Newton’s Law:
∑Fs=mas
Here all the frictional forces and effects are neglected. The forces that are acting in the s directions are pressure forces and they are acting from both sides along with the weight of the particle.
The equations will now become:
PdA-P+dPdA-Wsin =mVdVds (1)
Here is the angle between the normal of streamline and the vertical z-axis. The value of mass is m=ρV and it will become:
m=ρdAds
The value of the weight of the fluid particle will be W=mg and it will become:
W=ρ g dA ds
The value of theta will become:
sin =dzds
We will substitute all the values in equation 1 and we will get:
-dPdA-ρg dA ds dzds= ρ dA ds VdVds
Now the next step is to cancel out the dA and we will get the following equation:
-dP-ρg dz=ρV dV
In the next step we will substitute the value of V as
VdV=12dV2
We will substitute the value in the above equation and then divide each term by density and will get the following result:
dP+12d(V2)+gdz=0
After the integration the equation for the steady flow along the streamline will be as follows:
∫dP+V22+gz=constant
In the case of incompressible and steady flow the equation will be as follows:
P+V22+gz=constant
The above equation is used in inviscid flow regions. So now Bernoulli’s equation will be as follows:
P1+V122+gz1=P2+V222+gz2
This is the final equation of Bernoulli and that is derived by the conservation of momentum that is moving along the streamline.
Bernoulli’s Equation is also viewed as the Conservation of Mechanical Energy Principle.
This principle also states that no mechanical and thermal energy is converted but they are conserved separately.
Bernoulli’s equation is implemented to an incompressible, steady flow as we have discussed earlier.
As we have also discussed that whenever the force is applied to a system the energy is transferred so we can relate that with Bernoulli’s equation which statements will; be as follows:
The work done by the pressure and the gravitational forces that are increased is equal to the increase in the kinetic energy of fluid particles.
Force balance across Streamlines
In steady and incompressible flows, the force balance in the direction of n across the streamline is as follows:
P+∫V2Rdn +gz= constant
Unsteady and Compressible Flow
We have a huge discussion on the incompressible and steady flows and their derivation equation now Bernoulli’s equations in terms of compressible and unsteady flows are as follows:
∫dP+∫∂V∂tds+V22+gz=constant
Static, Dynamics and Stagnation Pressure
Some of the important key points related to the topics are as follows:
The statement of Bernoulli’s equations says that the sum of the fluid particle,s' kinetic, potential and flow energy is constant. So the kinetic and the potential energy during the flow is easily converted to the flow energy , which changes the pressure. So density is multiplied with Bernoulli’s equation and we got the following answer.
P+ρV22+ρgz=constant
this equation has some essential terms, and one by one, I will explain each term to you.
Static Pressure
At the start of the equation, there is pressure P, and that pressure is called Static Pressure. This static pressure does not incorporate dynamic effects. Static pressure is the accurate presentation of thermodynamics pressure, and while solving the equation, we use thermodynamics tables for using the values.
Dynamics Pressure
The second term, i.e. V22, is called the dynamics pressure, and when the fluid is in motion, and there is an increase in pressure, this pressure stops isentropically.
Hydrostatic Pressure
The third term of the equation is called hydrostatic pressure, and basically, this is not the pressure because of its dependence on elevation effects. This means that this pressure accounts for the weight of fluids.
so the sum of all these pressures is called total pressure, whereas the sum of static and dynamic pressure is known as stagnation pressure, and its equation is as follows:
Pstag=P+ρV22
Limitation of Bernoulli’s Equation
There are certain limitations applied while dealing with Bernoulli’s Equation. The list of constraints is as follows:
The first and foremost important limitation is that as we have derived the whole derivation of Bernoulli’s equation, you might have noticed the word steady and incompressible. So yes, Bernoulli’s equation is applicable in stable flows only. I have also mentioned the equation for unsteady flows also but there Bernoulli is not applicable.
You might have noticed one of the important factors that during the steady and incompressible flows, all the frictional and compressible effects are neglected. So yes, that is the second limitation of Bernoulli’s equation. Frictional effects in the case of short flows and large cross-sectional areas. And if the velocity is low, then that is a plus point. A slight disruption in the streamlined flow can make Bernoulli’s equation inapplicable to that flow. So much concentration and care are required for a steady and incompressible flow.
We have derived Bernoulli’s Equation from a particle moving along a streamline, so any flow in machines such as turbine fan or impeller without streamlined flow does not apply Bernoulli’s equations in flow sections. So energy equations are widely used for calculating the shaft input or output of these machines. But Bernoulli’s equation can still apply to flow sections before or past a machine.
The following restriction of Bernoulli’s equation is that Bernoulli’s equation states that density is constant, which means that the flow is incompressible. The incompressibility is applied in the case of liquids as well as gases. The Mach number should be less than 0.3 in that case. The compressibility and the density variations in the case of gases are negligible because of the low relative velocity.
Another limitation says that the increase in temperature decreases the density and vice versa. So Bernoulli’s equation is not applicable in the case where the flow section has a lot of changes in temperature (cooling and heating).
The last limitation of Bernoulli’s equation is that it is applicable in the flow streams only. As discussed above in the derivation, the final equation is applicable in the steady incompressible and flow streamline. So when the flow is disrupted or is irrotational there is no voracity in the flow field, the value of constant is the same for all the streamlines and here Bernoulli’s equation becomes applicable. The main thing is whether the flow is irrotational we don’t need to worry about the application of Bernoulli’s equation.
Application of Bernoulli’s Equation
Bernoulli’s equations are one of the most important fields and have numerous numbers of uses in our daily life. Here I will share some of the important applications of Bernoulli’s Equation. So let us start.
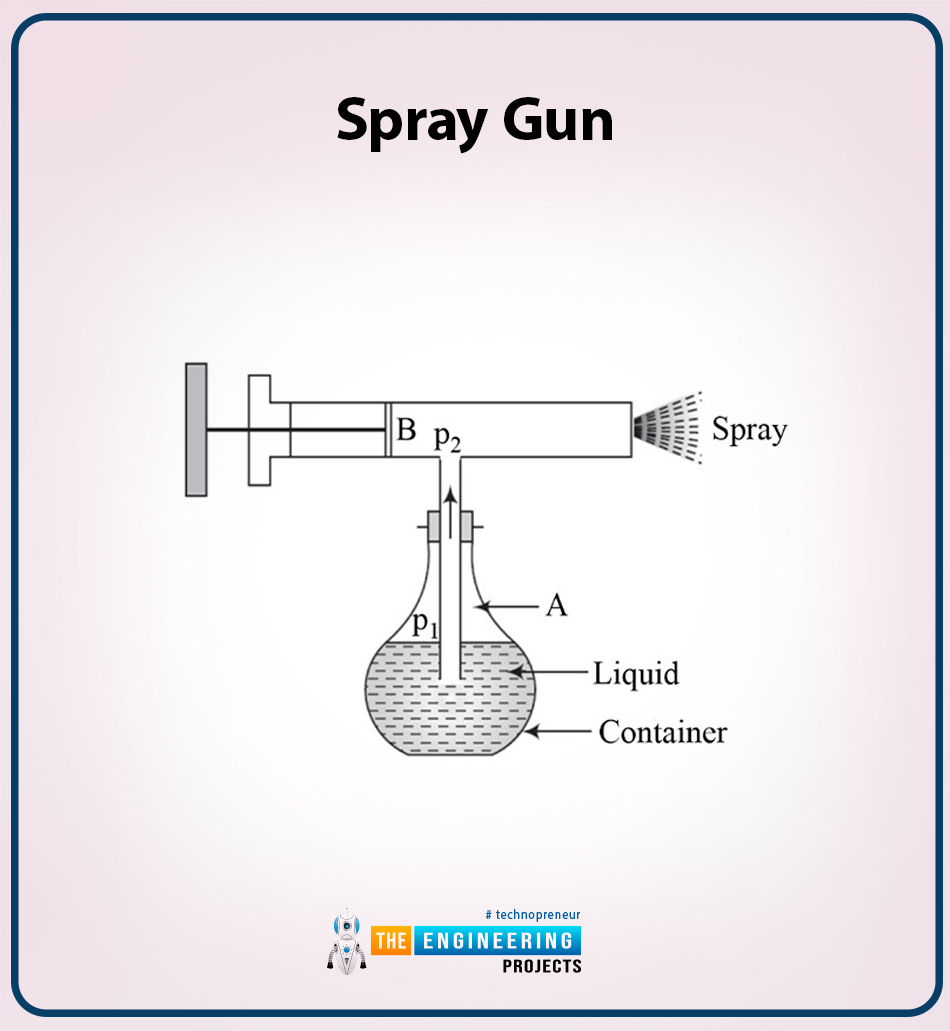
Spray Gun
One of the important applications of the Bernoulli’s Equation is a spray gun and another name is atomizer. The procedure is that we press the piston and the air is rushed from a tube that is in horizontal direction. The following diagram shows the atomizer.
So at point B, the air rushes out and the pressure is decreased from p2 to p1. Because of the pressure decrease, the liquid is raised in vertical tube A. So the high air pressure collides with the liquid rise tube and results in fine sprays. This fine spray is used in many different sprays, Bunsen burners, perfumes and many more sprays.
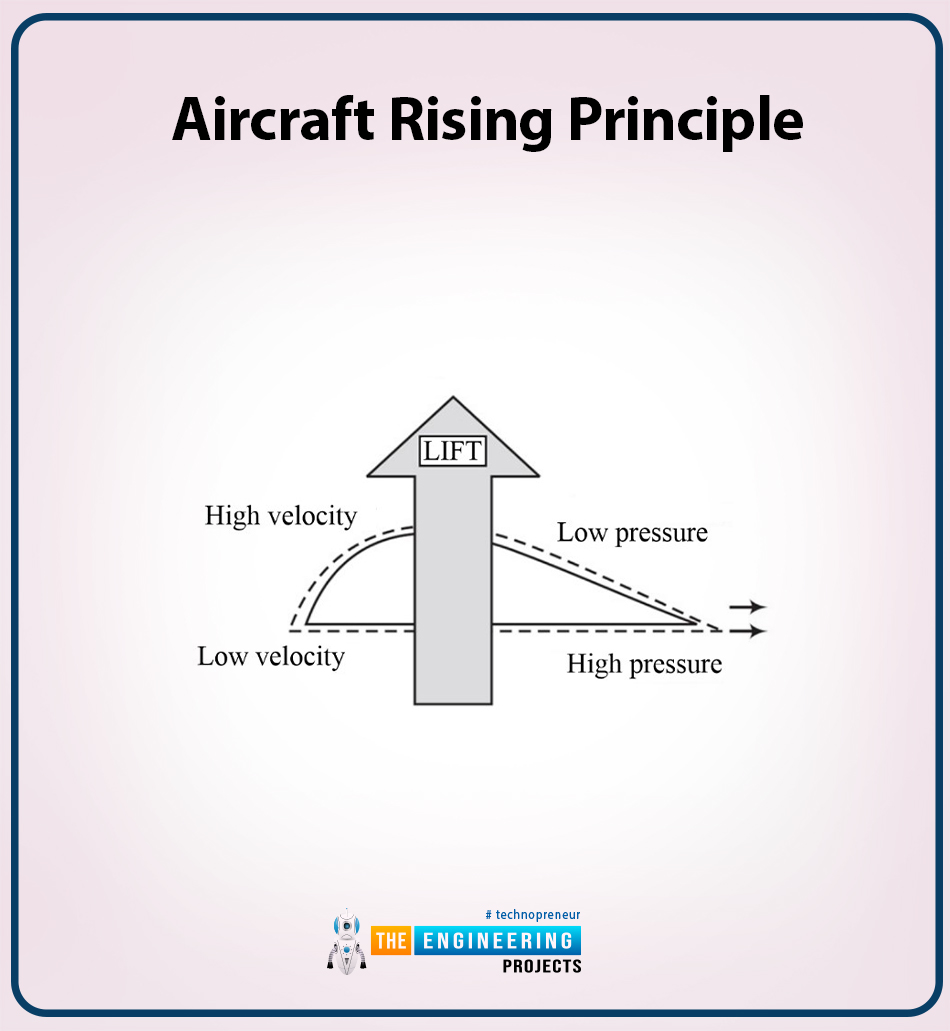
Aircraft Rising Principle
Who does not like travelling on aeroplanes? But do you know how aeroplanes take off and land? let me explain to you the theory of rising aeroplanes. Actually, the aeroplane rise as a result of the lift force that is acting on the wings. The lift is a result of an object placed asymmetrically and that is moving through the fluid. Bernoulli’s equation says that the increase or decrease in the velocity affects the pressure and causes variations in it. So pressure variations create an upwards force and that upward force is shown in the following diagram.
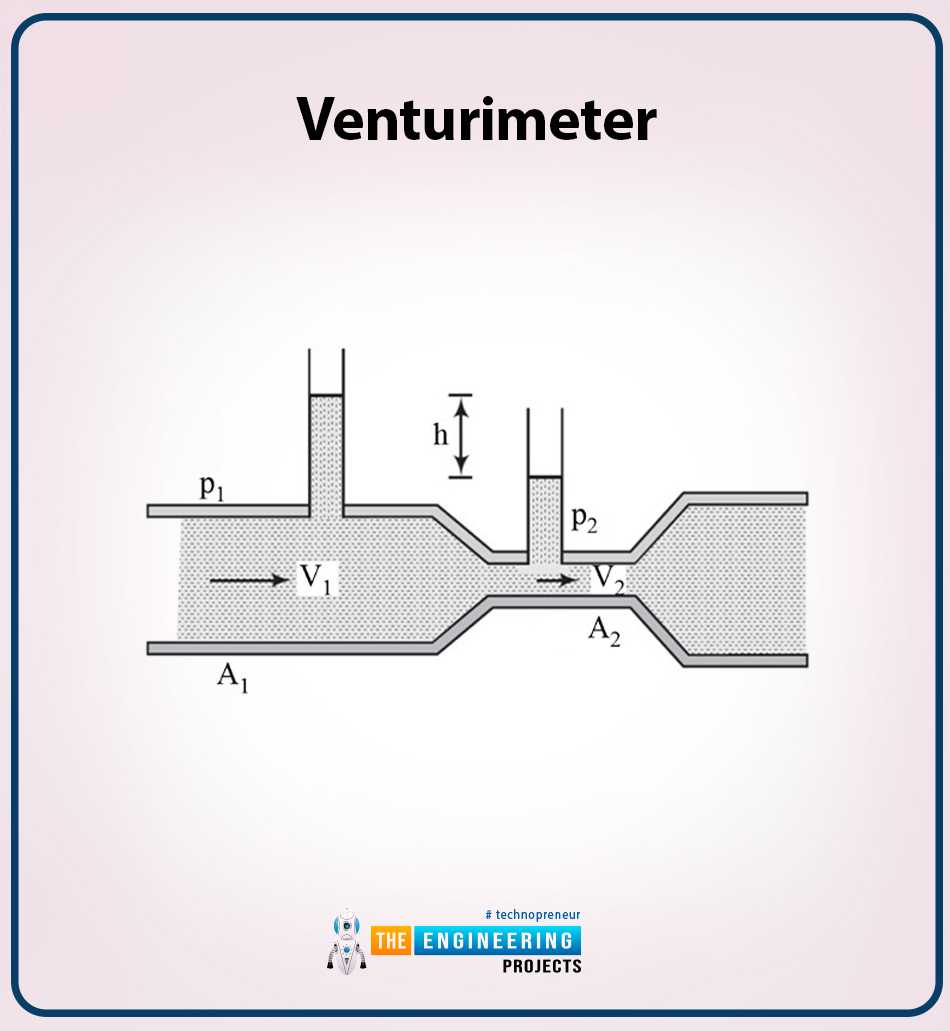
Venturimeter
This is also one of the well-known examples of Bernoulli’s equation. A Venturimeter is used for the measurement of flow speeds in the pipe that is not uniform. As we know that Bernoulli’s equation is applied in narrow shallow and wide pipes where the height is the same and the area at the inlet is greater than the outlet and the velocity at the outlet is greater than the inlet velocity and at last, the pressure at the outlet is greater than the pressure at the inlet. so there is a collectively force applied when the fluid enters the throat and the force slows down on leaving. The following diagram shows the working.
Now we will move towards our last topic of this article that is about the Energy Equation. This topic is also one of the fundamental topics of fluid dynamics. So without wasting any time let us start the topic and see the equations of it.