
Flow visualization widely uses Computational Fluid Dynamics (CFD) and physical experiments. So following are the types of patterns that can be visualized computationally and experimentally. So without wasting any time, let us start.
Streamlines and Streamtubes
There are two patterns. I will first explain the streamlines. So the definition of streamlines is as follows:
A streamline is a curve that is tangent everywhere to the instantaneous local velocity vector.
You might not understand the definition by reading it, so just for your ease, let me explain to you in few key points:
A streamline defines fluid’s motion throughout the flow field.
A streamline acts as an indicator of the instantaneous direction of motion of the fluid. To explain this situation, let me exemplify it with an example.
For instance, when we throw water on a solid surface, we observe the fluid flow pattern on the wall. That pattern is a streamlined pan in which the water is separated, moved in recirculating motion, or coming off the wall.
There is an equation of streamline; let me explain the background of the equation to you. Before that, have a look at the diagram.
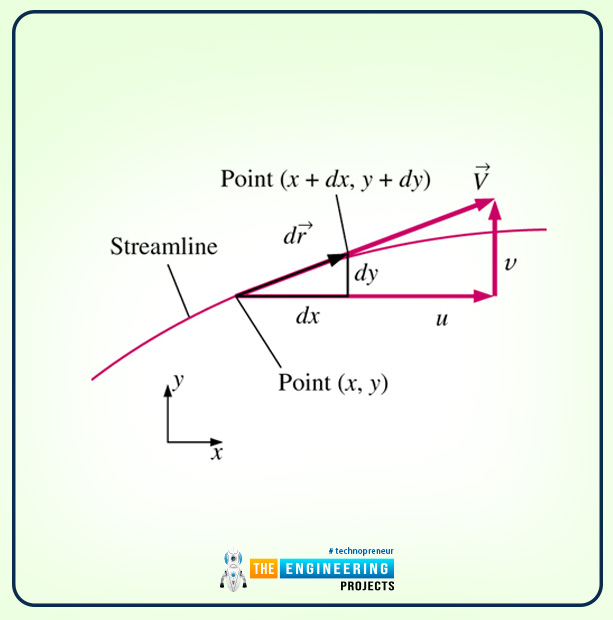
As you can see, there is an infinitesimal arc along the streamline. Here the infinitesimal arc length is as follows:
dr=dxi+dyj +dzk
Here is a condition that dr should be parallel to the local velocity, whose equation is as follows:
V=ui+vj +wk
By utilising the geometric rules, infinitesimal arc dr is proportional to the local velocity, and the equation of streamline will be like this:
drV=dxu=dyv=dzw
Here, dr is the magnitude of infinitesimal arc length, and V is the magnitude of velocity.
To obtain the equation in an (x, y) plane, we will integrate equation 1 and get the equation of streamline in an (x, y) plane. The equation is as follows:
(dydx)along astreamline=vu
Now I will give a brief explanation about the Streamtubes. So the definition of Streamtubes is as follows:
A Streamtubes is a bundle of streamlines similar to the communication cable with optic fibre cables.
You might not understand the definition by reading it, so just for your ease, let me explain to you in few key points:
As I have discussed earlier, streamlines are parallel to the local velocity, so according to the theoretical information, the fluid cannot cross the streamlines.
A simple diagram elaborates on tee difference between the streamlines and streamtubes.

Pathlines
The definition of Pathlines is as follows:
A Pathline is an actual path travelled by an individual particle (obviously a fluid particle) at some time period.
The following are some essential key points related to the pathlines:
You might have noticed one thing while reading the definition of pathline and Lagrangian are much similar. Both follow a path of an individual particle when the fluid flows.
There is a technique named Particle Image Velocimetry (PIV) that is used to measure the velocity field in one flow of a specific plane.
Let me explain to you the PIV technique briefly. So what happens in PIV is that those small particles are released in fluid, as shown in the diagram.

Then, the flow is observed by a two-flash light to make two spots on a film of every small particle moving. The magnitude and direction of the velocity of each particle location are fixed because the particle size is small. In today’s modern era of science and technology, many modern computers and digital photography have enabled this feature.
In order to trace the location of particles by the following equation:
x=xstart+tstarttV dt

So, the diagram mentioned earlier shows the pathline following the actual path of fluid particles.
There is a condition that if the velocity field is steady, the fluid particles are bound to follow the streamlines.
Streaklines
The definition of a streakline is as follows:
A streakline is the locus of fluid particles passed sequentially through the flow’s specific (prescribed) point.
The following are some important key points related to the streaklines:
The streaklines are one of the most common flow patterns produced through physical experiments. To explain this point more clearly, let me explain to you through an example. If we insert a tube (specifically in small size) in the flow and then add a continuous stream of tracer fluid, the pattern produced due to the addition will be streaklines. The flowing diagram shows the streaklines produced when the constant stream of tracer fluid (colored fluid) is added to the flow. The fact about the diagram is that the streaklines are similar to the pathline and streamlines.
Here is an interesting point to be noted: if the flow is steady, then the pathlines, streamline, and streaklines are all identical.
So you might be confused by the statement that pathlines, streamlines, and streaklines are similar in steady flow. But in the case of unsteady flow, the scenario is entirely different.
There is a difference, i.e., streamlines give an instantons flow pattern (by definition) but in the case of streaklines is an instantons snapshot of time-integrated flow patterns. And the pathlines are the time-exposed flow path of an individual particle at some time.
The equation to find the integrated tracer particle is as follows:
x=xinjection+tinjecttpresentV dt
Timelines
The definition of timelines is as follows:
A timeline is a set of adjacent fluid particles that were marked at the same time.
The following are some key points related to the timeline:
The fluid flows in which there is uniformity and a steady flow, then timelines are observed.
Practically timelines can be generated in any water channel with the help of hydrogen bubble wire.
Plots of Fluid Flow Data
As we all know, flow properties vary from time to time, and in space, it is necessary to plot flow data in various ways. In this article, I am going to explain three kinds of plots that are profile plots, vector plots, and contour plots, respectively.
So without wasting any time, let’s start explaining the plots.
Profile Plots
The definition of a profile plot is as follows:
A profile plot indicates how the scalar property varies along some desired direction in the flow field.
The following are some essential key points related to profile plots:
It is one of the simplest plots much similar to the XY-plots.
As the definition describe that the profile plots are created for the scalar quantities, but in fluid mechanics, velocity profile plots are used. As velocity is a vector quantity. So, to create a profile plot, we either use magnitude or velocity.
Vector Plots
The definition of the vector plots is as follows:
A vector plot is an array of arrows reflecting the magnitude along with the direction of vector quantity at an instant of time.
The following are some essential points related to the vector plots:
Streamlines are used to present the direction of the instantaneous velocity; here, they do not show the velocity magnitude.
A flow pattern is a vector plot for experimental and computational fluid flow. They have an array of arrows that indicate both magnitude and direction of a vector quantity.
Contour Plots
The following definition of a contour plot is as follows:
A contour plot shows curves of constant values of scalar property (or magnitude of a vector property) at an instant in time.
The following are some essential key points related to the contour plots:
The contour plot may have curves indicating various properties called Contour Line Plot.
Some of the contours are filled with color of grey are called Filled Contour Plot.
Kinematic Descriptions
In fluid mechanics, the elements have four fundamental types of motion or deformation in two dimensional as follows. It is interesting to know the fact that all four of these motions can act at the same time. Yes, you heard it right. Isn’t it amazing? In fluid dynamics, the motion and deformation of liquid elements at different times are described. So the deformation rates are expressed in terms of velocity and derivatives of velocity.
Translation
Rotation
Linear Strain (Extensional Strain)
Shear Strain
So let us start explaining one by one.
Translation
The translator and rotatory motion are one of the most common motions that are observed in our daily life. For the three dimensions, a vector is used to define the translator rate. In Cartesian coordinates the rate of translation is as follows:
V=ui+vj+wk
Rotation
The rate of rotation or the angular velocity is defined to be the average rotation rate of two perpendicular lines that intersects at some point.
Example:
In order to exemplify this whole situation, let us explain through some examples.
Let us take an initially square fluid element and consider its bottttttttt.
Technically, the left and the bottom edge of the element intersect at some point. Thus we can say that they are perpendicular to each other.
Now, these two lines tend to rotate in a counterclockwise direction (which is said to be the positive direction).
Toto, show a clearer picture to you let me show you a diagram. So the below-mentioned diagram explains the rotational effect.
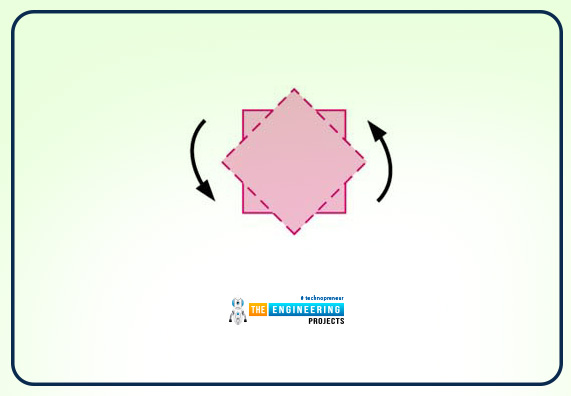
One of the main points to observe is that the angle between the two lines remains the same, which is 90 degrees.
So the line rotates at the same rate of rotation.
Here there is also one of the most essential points about the rate of rotation is that when the case is two dimensional then the fluid elements move in translator motion and then rotate. But while rotating, they deform easily.
In order to calculate the rate of rotation, the whole thing is calculated by the scenarios mentioned above, i.e. two lines are taken named a and b respectively. These two lines intersect at a specific point called P ( as mentioned above that this procedure is in two dimensions. Which Means that they are in the XY plane).
These lines are being followed and rotated in an infinitesimal increment of time, and that is:
dt=t2-t1
Line a rotates at some angle aand line b also rotates at a specific angle b. The average rotation angle will be:
a+b2
So the final equation will be as follows:
ω=ddt(a+b2)
ω=12(∂v∂x-∂u∂y)
Linear Strain Rate
The definition of linear strain rate is as follows:
Linear strain rate is defined as the rate of increase in length per unit length.
Some of the important key points related to the linear strain rate are as follows:
The linear strain rate depends upon the direction of the line segment and this line segment measures the linear strain.
But here important point should be kept in mind i.e. that the linear strain rate cannot be defined as vector or scalar quantity.
The linear strain rate can be defined in an arbitrary direction.
The linear strain rate can be defined in Cartesian coordinates by the formula as follows:
xx=∂u∂x yy=∂v∂y zz=∂w∂z
Volumetric Strain Rate
The definition of the volumetric strain rate is as follows:
The rate of increase in the volume of fluid element per unit volume is called the volumetric strain rate.
Some of the important critical points related to the volumetric strain rate are as follows:
In an incompressible flow, the volumetric strain rate is zero.
With the increase in volume, the kinematic property is always positive.
The other definition word for the volumetric strain rate is called Rate of Volumetric Dilatation.
The rate of volumetric dilatation is remembered by an example. Let us take an example of the iris of expands enlarging when there is less light.
The formula of volumetric strain rate in Cartesian coordinates is as follows:
1VDVDt=1VdVdt=xx+yy+zz=∂u∂x+∂v∂y+∂w∂z
Shear Strain Rate
The definition of the shear strain rate is as follows:
A shear strain rate is defined at the point as half of the rate of decrease of the angle between two initially perpendicular lines that intersects at some points.
Some of the important key points related to the shear strain rate are as follows:
In order to explain the definition, let us explain through some examples. Let us see a diagram first that is mentioned below:
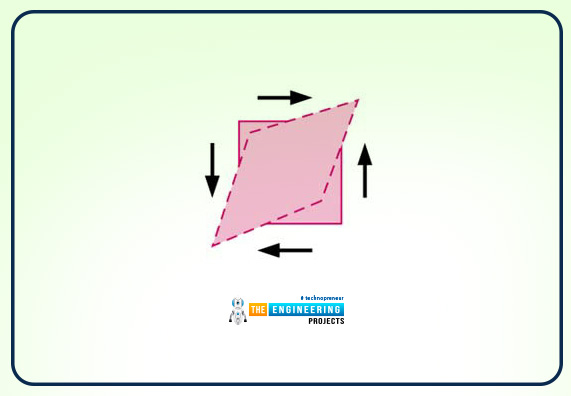
In this diagram, the angle is at first 90 in the lower left corner and upper right corner of the element of fluid the angle decreases so that is a positive shear strain. But the angles at the upper-left and lower-right square fluid element increase so that is negative shear strain.
In the Cartesian coordinates system, the shear strain rate will be:
xy=12∂u∂x+∂v∂x zx=12∂w∂x+∂u∂z yz=12∂v∂z+∂w∂y
Conclusion:
I hope you have learned a lot through this article. Thank you for reading.




