In this article, I will explain the differential equations of fluid motion, i.e., conservation of mass (the continuity equation. So without wasting any time, let us start.
What is differential Analysis?
As a part of this article, it is essential to know what differential analysis is and how we can apply it to explain continuity and Naiver Stroke’s theorem.
Some of the essential key points related to the differential analysis are as follows:
Differential analysis is the application of a differential equation of fluid motion to any or every point in the flow field over a region called the Flow Domain.
Some readers might confuse the word differential with the small control volumes piled up on each other in the flow field.
Whenever the size of the control volume crosses the limit and extends to infinity, then the size of each control volume becomes so small that the conservation equations simplify to a set of partial differential equations. These partial equations can easily be applicable whenever required in any flow field.
As I have discussed earlier, two differential equations, the Law of Conservation of Mass (Continuity Equation) and Newton’s Second Law (Naiver Strokes Equation), are the ones on which there is a drastic change in the temperature and density such kind of equations are easily solved with the help of differential equation.
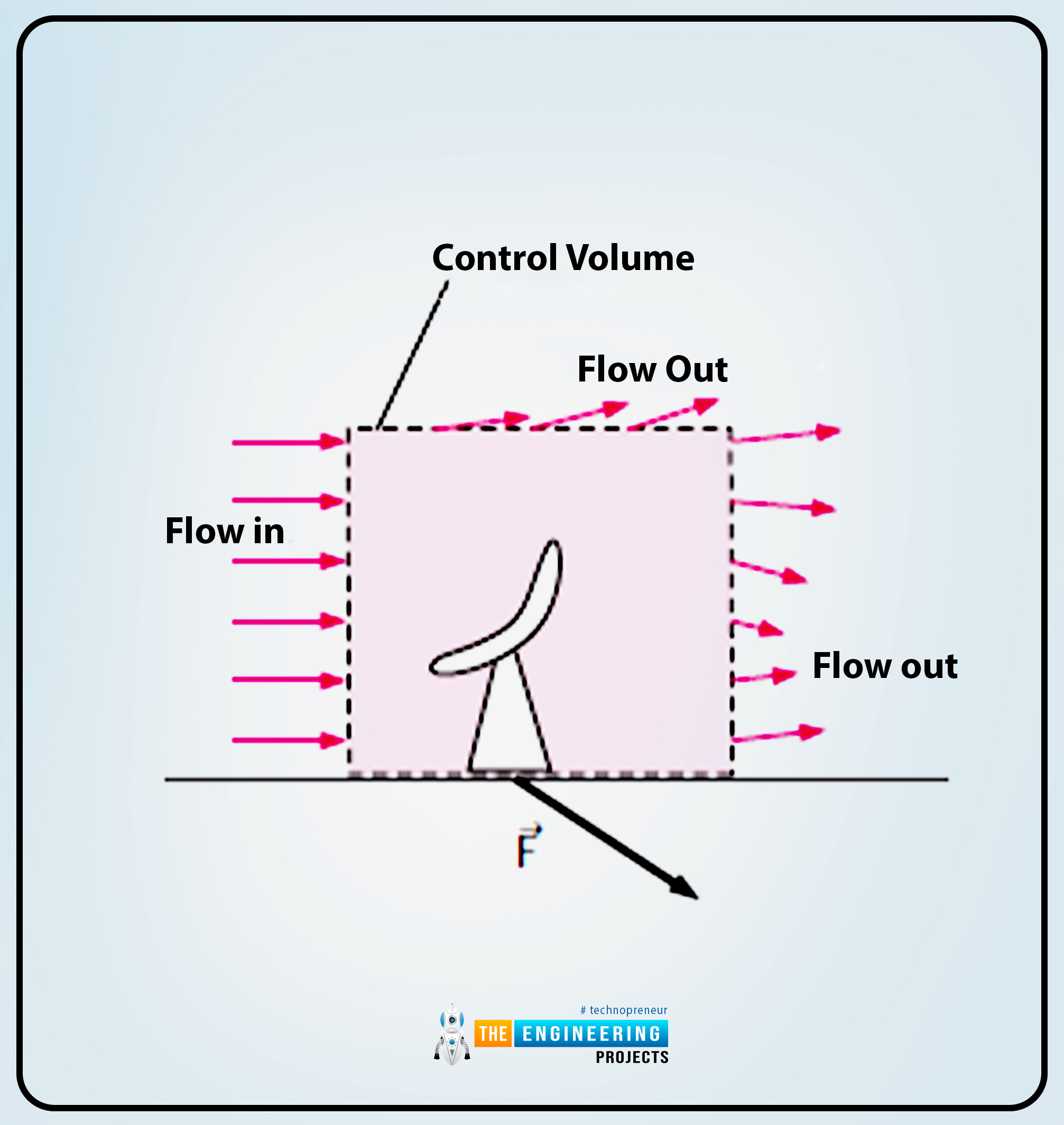
The following diagram shows the study of control volume in which the control volume seems to be much similar to the black box.
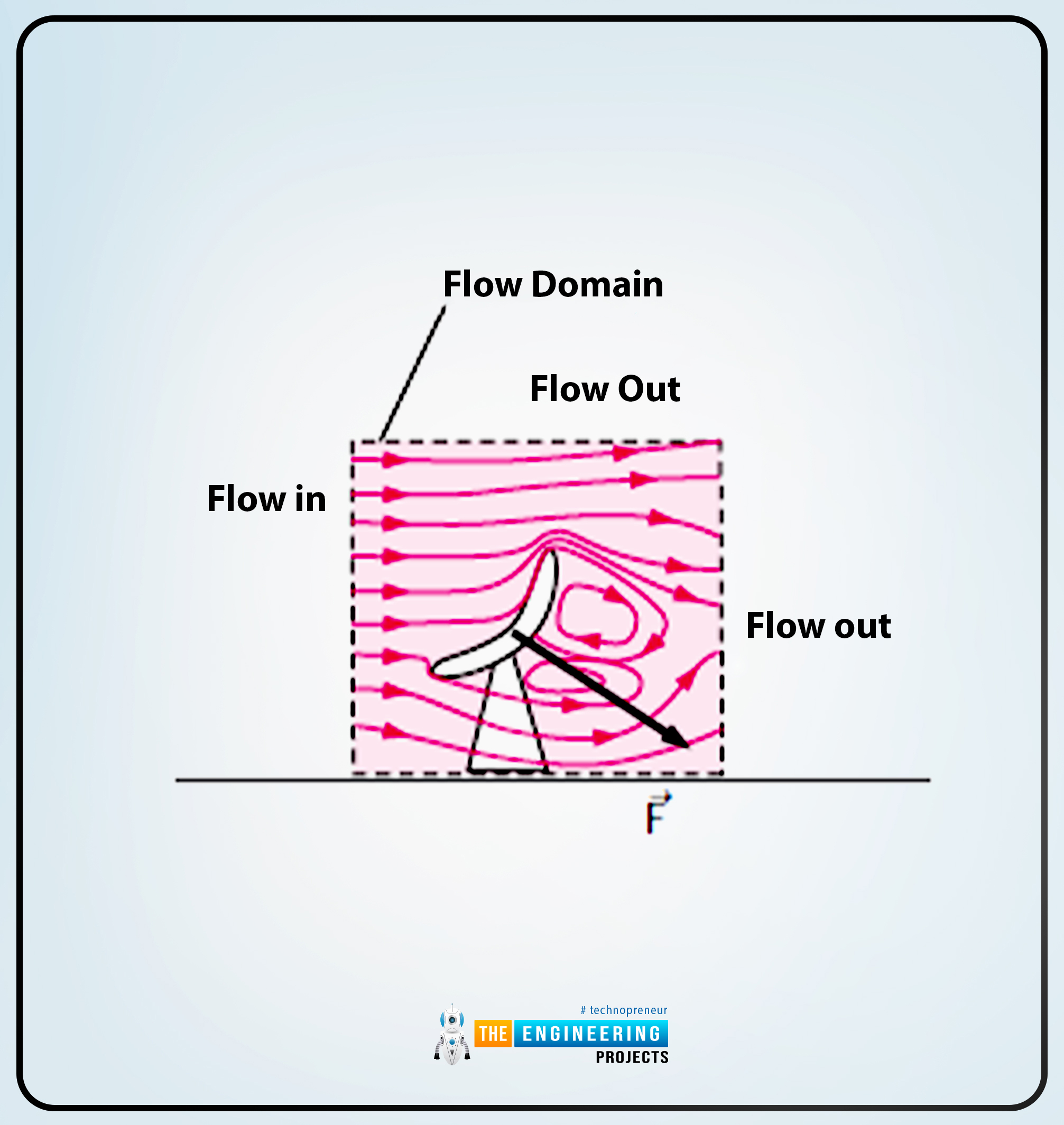
Now, the second diagram shows that all the flow points are solved within the flow domain in the case of differential analysis.
While solving the differential equation in the case of incompressible flow, there are about four unknown, i.e., velocity components (u, v, w), one pressure component, and four equations (three equations from Naiver Strokes Law and one from Law of Conservation of Mass).
There are variables and constants in equations, but in differential equations, all the variables are solved at once because, in such situations, the equations are coupled. Now, what is coupled, and how are equations coupled? We will see it in the upcoming topics.
While solving the differential equation, the boundary conditions must be defined.
We are moving towards the first important part of our article, i.e., the Law of Conservation of Mass. Let us start.
Conservation of Mass–Continuity Equation
In one of my previous articles, I have extensively explained the conservation of mass. But now, here, I will explain the derivation in terms of the infinitesimal control volume by the divergence theorem. So let’s start.
To explain the topic, I will divide it into essential critical points in the following way.
First of all, let us recall the conservation of the mass equation through the application of Reynold’s Transport Theorem;
0=∫CV∂ρ∂t dV+∫CSV.n dA (a)
The equation is for the fixed and control volumes.
In the case of well-defined and selected inlets and outlets, the equation will be as follows:
∫CV∂ρ∂tdV=inm-outn (b)
The above equation explains that the rate of change of mass within the control volume equals the rate at which mass flows into the control volume subtracting the rate with mass flow out of the control volume.
Now I will explain the derivation using the divergence theorem.
Derivation Using the Divergence Theorem:
The other name of the divergence theorem is called Gauss’s Theorem.
The statement of the divergence theorem is as follows:
The Divergence Theorem (Gauss’s Theorem) is used to transform a volume integral of the divergence of a vector into an area integral over the surface that defines the volume.
Some of the essential key points related to the Divergence theorem are as follows:
Mathematically, the divergence theorem is defined as the divergence G and can be written as follows:
∫vV.GdV=∮AG.n dA (c)
There are two kinds of integration in the equation one is simple, and the other has circled it. This indicates that the entire area surrounds the volume. So as you can see that the equation is beneficial in gaining data.
The primary purpose of using the divergence theorem is to transform the volume integral of the divergence vector into an area integral over the surface, and that surface defines the volume.
In the case of any vector, the divergence will be defined as a G, and the equation as m will be used to describe it.
In some cases, we also define the divergence as follows:
G=ρV
We can also define it by playing with the values, and for that, we substitute the value of equation (c) into equation (a), and we will get the results as follows:
0=∫cv∂ρ∂t dV+∫cvV. (ρV) dV
As you can see that there are two integrals, so to get the required equation, we will combine the two integrals into one and then the result will be as follows:
∫cv∂ρ∂t+V. VdV=0
Now, we come to the conclusion that the equation that is mentioned above is for the control volumes, regardless of any size and shape.
So, the statement above is only possible if the terms within the brackets are identically zero.
Moving towards the critical statement, i.e. the equation of continuity. So the general differential equation for the conservation of mass is also known as the continuity equation, and the equation is as follows:
∂ρ∂t+V. V=0
So, this is the equation of continuity. This equation is for compressible flows only and does not implement for incompressible ones; the -mentioned equation ensures the validity of the flow domain point.
Now that is all from the derivation using the divergence theorem. The next topic is also a part of it. Have a look.
Derivation using an Infinitesimal Control Volume
The continuity theorem is defined in different ways, and one of them will describe by me. The continuity theorem starts with the control volume, and, taking it as a base, I will tell the whole topic.
So following are some essential key points related to the topic:
We will start with the assumption. Let us consider an infinitesimal box that controls volume and aligns with the axes in the Cartesian Coordinates system.
The following is the diagram that shows the box-shaped control volume.
As you can see from the diagram along the x-direction, the length is mentioned as dx, in the y-direction as dy and along the z-direction as the dz, respectively.
Moreover, at the centre of the box, there is information that says that the density is defined as a symbol and the velocity is defined in velocity components as u, v, and w, respectively.
So, we use Taylor's Theorem within the box at different locations away from the centre. And to define this point, we will use an example as follows:
(u)centre of right face=ρu+∂(ρu)∂xdx2+12!2(ρu)x2(dx2)2
In the case of the above-mentioned equation, the control volume has just limited to a point only, and the higher power or even the second power terms are negligible.
So, for the six faces of the box, we use the Taylor series expansion to density times the normal velocity component at the central point of each of the six faces, so they are as follows:
Center of Right Face
(u)centre of right face≅ ρu+∂(ρu)∂xdx2
Centre of left face
(u)centre of left face≅ ρu-∂(ρu)∂xdx2
Centre of Front Face
(w)centre of front face≅ ρw+∂(ρw)∂zdz2
Center of Rear Face
(w)centre of rear face≅ ρw-∂(ρw)∂zdz2
Center of Top face
(v)centre of top face≅ ρv+∂(ρv)∂ydy2
Center of Bottom face
(v)centre of bottom face≅ ρv-∂(ρv)∂ydy2
Now, there is another statement that says that
The mass flow rate into or out of the faces of the box is equal to the density times the normal velocity components at the centre point of the face times the surface area of the face.
We can define it as mathematically as follows:
m=VnA
The above equation is valid for each face. The Vn shows the magnitude of the normal velocity through the face, and the A shows the surface areas of the face.
The following diagram shows the mass flow rate through each face of our infinitesimal control volume; you will easily get the idea about it:
So all the theoretical background that I have mentioned in the diagram that is above can be easily understandable by the diagram.
For all the nonnormal velocity components, the truncated Taylor series expansions at the centre of each face can also be defined. But we have not represented as these components are tangential to the face.
Now we will move towards another equation, and that equation says the control volume shrinks at any of a point, and the value of the volume integral on the left side of the equation (b) will become as follows:
∫cv∂ρ∂t dV≅∂ρ∂tdxdydz
As we know that the volume of the box is dx, dy, and dz, respectively.
Here is a trick: with the help of the diagram, we can apply the approximations from the figure to the right side of the equation mentioned above. In this case, we will add all the mass flow rates at the inlet and the outlet of the control volume through all of the faces. Then take a left, bottom, and back faces contributing to the mass flow rate. Then concerning the equation, the right side will be as follows:
inm≅(ρu-ρu∂xdx2)dydz+ρv-ρv∂ydy2dxdz+(ρw-ρw∂zdz2)dxdy
The following are the faces that are mentioned in the equation:
Left Face =ρu-ρu∂xdx2dydz
Bottom Face=ρv-ρv∂ydy2
Rear Face=(ρw-ρw∂zdz2)dxdy
The next topic is also part of the Continuity Equation. So without wasting any time, let us start.
Alternative Form of the Continuity Equation
There is also an alternative way to present the continuity equation as we know that the following equation is according to the product rule of divergence theorem:
∂ρ∂t+V. V=∂ρ∂t+V. ρ+ρ.V=0
In order to explain the continuity equation alternative way, I will explain it in a few important key points:
The following is the alternative form of presenting the continuity equation:
1DρDt+.V=0
The above-mentioned equations show the fluid element that is flowing through the flow field, and it is also called the material element. Here there is a change that the .V is the change in the density.
So we can say that if the change in the density of the material element (fluid element) is small as compared to the magnitudes of the velocity gradient in the .V also if the element moves around, then the flow is said to be incompressible, and it is limited to it only.
So that is all from the alternative way of presenting the continuity equation. Now the next topic is another part of presenting the continuity equation.
Continuity Equation in Cylindrical Coordinates
The cylindrical polar coordinates system is a way of presenting the terms in (r,,z). it is also known as the cylindrical coordinates system.
In this topic, I will show you how the terms can be explained in a cylindrical system, and it is another way of presenting the continuity equation. So following are some of the important key points related to the topic. Have a look at it:
There can be three-dimensional, one-dimensional and two-dimensional cylindrical coordinates, but here in this topic at the start, I will explain in terms of the two-coordinates system only.
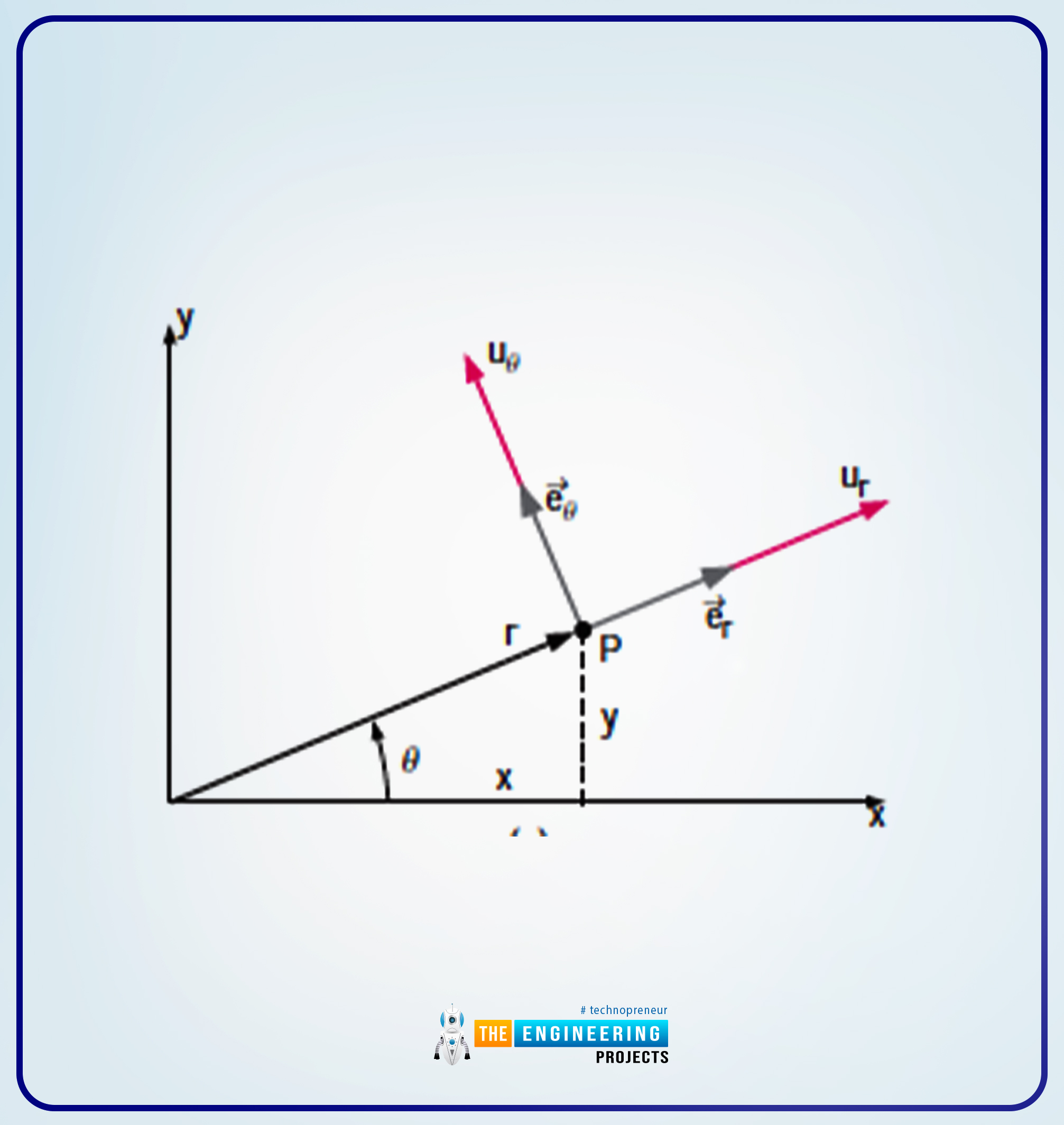
The following are the explanation of the (r, θ):
Here, r shows the radial distance i.e., from the origin to any point (let us say P).
Then there comes , now which shows the angular measurement from the x-axis (if we talk about generally, then is defined as a positive value, and it is in a counterclockwise direction).
The following is a figure that shows the complete explanation of the theoretical background:
There are more important terminologies that need to be defined. So following is the explanation of it:
ur and u are the velocity components
er and e are the unit vectors.
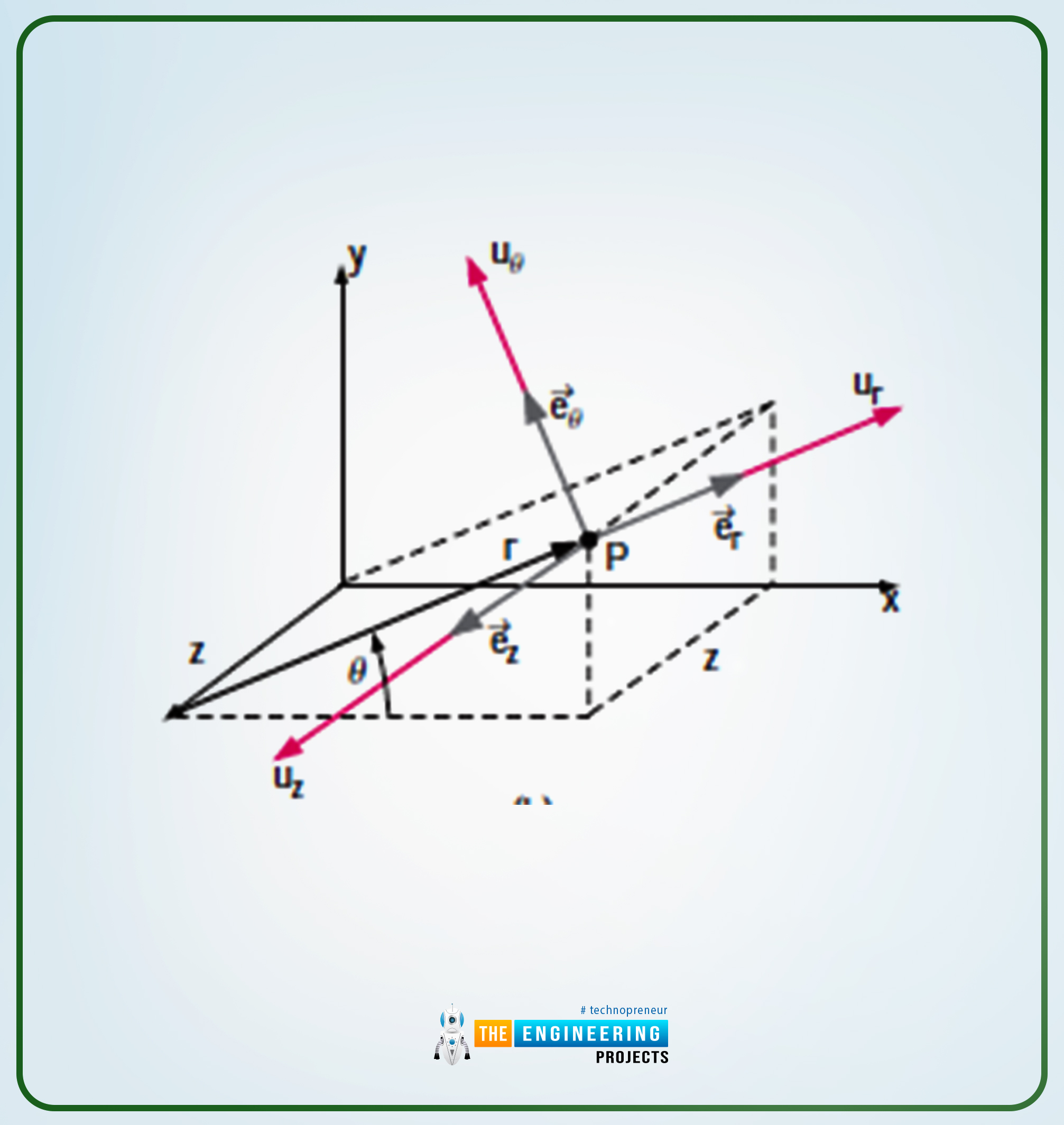
In the case of three-dimensional, there is obviously a z-axis. So in order to show the points, the following diagrams explain well. Have a look at it.
So as you can see that in the three-dimension case, there are two more values, one for the velocity component and the second for the unit vector.
So the following equation shows the coordinate transformation:
r=x2+y2
x=rcos
y=sin
θ=yx
So following is the equation that expresses the continuity equation in terms of cylindrical coordinates.
∂ρ∂t+1r(rρur)r+1r(rρu)+1r(rρuz)z =0
Thank you for reading.