Hexapod Simulation in MATLAB

I have designed this project on a client's request and today I thought to share it with you guys. Because this Hexapod simulation in MATLAB is designed after a lot of efforts by our TEP team that's why this simulation is not free to download but we have placed a small price on it so that engineering students can buy it easily. So, let's get started with Hexapod Simulation in MATLAB.

Hexapod Simulation in MATLAB

• First of all, you need to buy this Hexapod Simulation in MATLAB by clicking the below button:

Buy This Simulation

• When you buy this project, you will get three files in it which are named as:
• Hexapod.m
• RobotMotion.m
• Robot Design.m
• You need to open the first one named as Hexapod.m, this is the Main file for this Hexapod Simulation in MATLAB.
• It has the below code in it:

clc;
clearvars;
close all;
imtool close all;
subplot(6,6,1:30)
xlabel('x'); ylabel('y'); zlabel('z'); 
axis([-150 200 -50 150 0 150])
grid on
hold on

Inc = 0;
firstLen = 50;
secondLen = 50;
stepSize = 20;
StepsTaken = 1;
y1 = 0;
y2 = 1;

RobotDesign(firstLen,secondLen)
subplot(6,6,31)
subplot(6,6,32)
subplot(6,6,33)
subplot(6,6,34)
subplot(6,6,35)
subplot(6,6,36)
OldInc = 0;
for b = 0:1:StepsTaken-1

subplot(6,6,1:30)
[Inc OldInc y1 y2]= RobotMotion(firstLen,secondLen,stepSize,Inc,OldInc, y1, y2);

end

• As you can see in the above code, we can set different parameters like lengths of legs and the steps it can take etc.
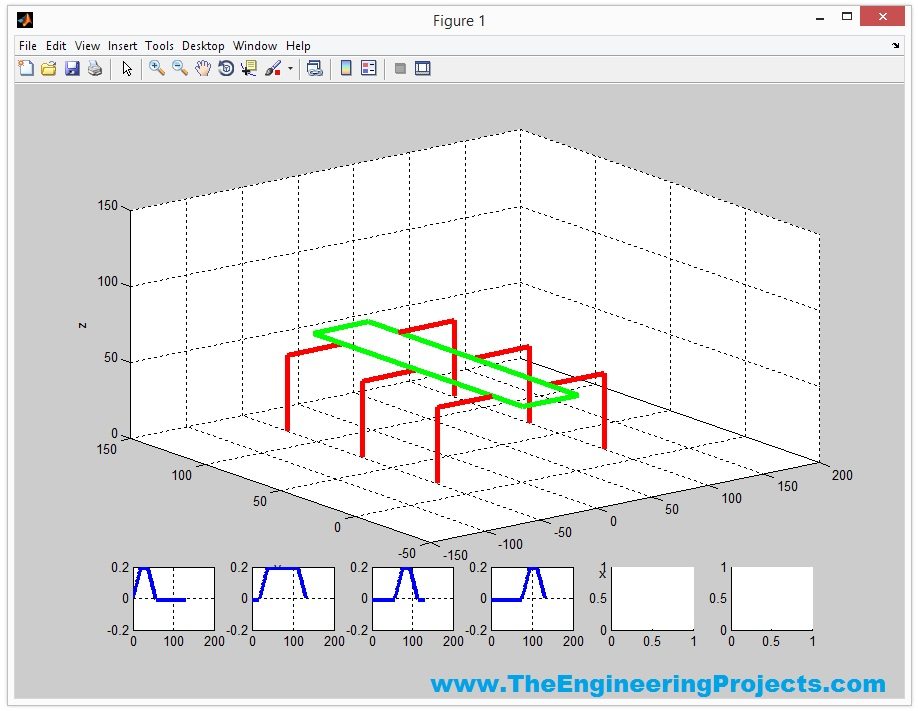
• Let me give a slight overview of Hexapod and how it works. So, have a look at below figure:

• I have designed a small hexapod and I have colored its legs.
• The red Color legs are called Gate 1 while the green color legs are called Gate 2.
• Now, when a Hexapod moves its first three legs (Gate 1) which I have designed in Red Color are first moved in upward motion and after that the Gate 1 moves in the Forward Direction and then finally Gate 1 moves in downward direction.
• After that the Gate 2 Legs are move in upward Direction and then Gate 2 Legs are moved in Forward Direction and finally Gate 2 moves in downward direction.
• Now when all legs are moved in Forward direction then finally the Robot Body is moved in Forward Direction.
• Let me summarize these steps:

1. Gate 1 (Red Legs) moves in Upward Direction.
2. Gate 1 (Red Legs) moves in Forward Direction.
3. Gate 1 (Red Legs) moves in Downward Direction.
4. Gate 2 (Green Legs) moves in Upward Direction.
5. Gate 2 (Green Legs) moves in Forward Direction.
6. Gate 2 (Green Legs) moves in Downward Direction.
7. Robot Body moves in Forward Direction.

• These are the 7 steps a hexapod takes to move a single step Forward.
• Now in the above code, I have used some variables which are:

1. firstLen = 50;
2. secondLen = 50;
3. stepSize = 20;
4. StepsTaken = 1;

• firstLen is the length of Gate 1 legs which I have set 50 rite now.
• secondLen is the length of Gate 2 legs.
• stepSize is how big the step should be.
• StepsTaken is how much steps it should take.
• Now when you run the simulation then the first thing you will get is shown in below figure:

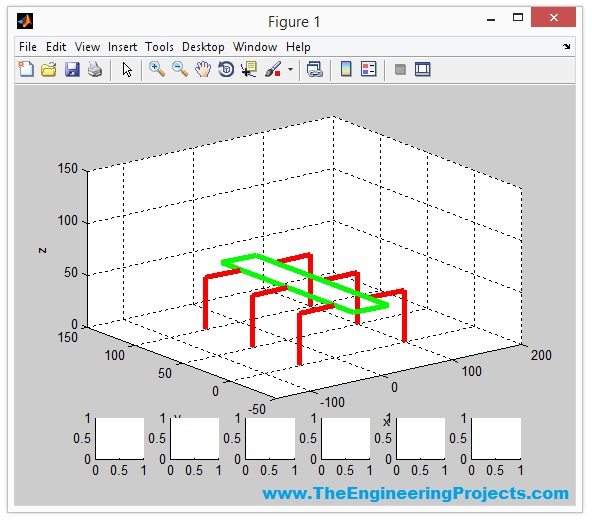
• AS I have given StepsTaken = 1 so it will just take one step, you can change it though and when it takes one step the final position of robot will be as shown in below figure:

• Now, if you compare the above two figures then you can see the starting position of Hexapod in x direction was 0 but when it took first step then now its position is 20.
• The below four graphs are showing the angles of your robot gates in radians.
• The below video will explain this project in detail: