Introduction to MATLAB

We would welcome all the scientists, engineers, hobbyists and students to this tutorial series. MATLAB is a great tool used by scientists and engineers for scientific computing and numerical simulations all over the world. It is also an academic software used by PhDs, Masters students and even advanced researchers.

MATLAB (or "MATrix LABoratory") is a programming language and numerical computing environment built by Mathworks and it’s first version was released in 1984. To this day, we keep getting yearly updates. MATLAB allows matrix data manipulations, plotting of symbolic functions as well as data, implementation of robust algorithms in very short development time, creation of graphical user interfaces for software development, and interfacing with programs written in almost any other language.

If you’re associated with a university, your university could provide you with a license.

You can even online now! You can simply access it on…

You can quickly access MATLAB at https://matlab.mathworks.com/ Here’s a small trick. You can sign up with any email and select the one month free trial to get quickly started with MATLAB online.

And in case you can’t have a license, there’s also Octave, which is a different programming language but very similar in all the fundamental aspects to MATLAB. Especially for the purposes of these tutorials, Octave will help you get started quickly and you can access it on: https://octave-online.net/#

Typical uses of MATLAB include:

1. Math and numerical computation from the MATLAB prompt
2. Developing algorithms and scripts using the MATLAB editor
3. Modeling and simulation using Simulink, and toolboxes
4. Data Visualisation and generating graphics
5. Application development, with interactive Graphical User Interface
6. Symbolic manipulation using MuPad

MATLAB is an interpreted high-level language. This means any command input into the MATLAB interpreter is compiled line by line, and output is given. This is useful for using MATLAB as a calculator as we will see in the next section.

Using MATLAB as an Advanced Calculator/ Beginner Commands

By default, the MATLAB Prompt will be visible to you. The two angled brackets ‘>>’ refer to the MATLAB Command Prompt. Think of this as the most basic calculator. In fact, whenever you look at this, think of it as a Djinn asking for an input from you.

Anything that you give it and press enter is known as a command. Whatever it outputs is known as the response. Whatever question you ask Matlab, it will be willing to respond quickly.

For example, in the figure below, I simply write the command ‘2+2’ and press enter, to get the answer ‘4’ as a response.

You can even define variables like you do in your algebraic geometry class.

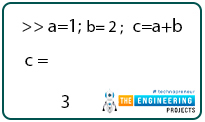
Notice that the semicolon ‘;’ that we see there is simply an indicator of when a statement ends like many other programming languages. Although this is not a necessary input in MATLAB, unlike many other languages which will simply give you an error if you forget this semicolon. Another function this serves is to suppress the output.

In MATLAB, you don’t need to ask for the answer or the result to be printed and it will continue to print by itself as part of the response. However, if you don’t want to see the output, you can suppress it.

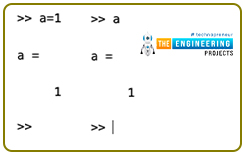
You can also look at the value stored in a variable by simply writing the variable name and pressing ‘enter’.

We can even create a matrix of numbers as shown in the image below. This can be a 1D matrix, or a 2D matrix. Notice the use of square brackets, commas and semicolons in order to create the matrix of numbers.

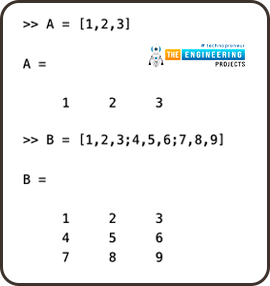
You can even create matrices of numbers which are 3D numbers or even higher dimensions. When we will learn about images, we’ll see how an image is just a collection of numbers, and simple manipulation of those matrices will help us in manipulation of images.

Saving Programs in MATLAB

You can write and save your own commands in the form of an ‘m-file’, which goes by the extension ‘.m’. You can write programs in the ‘Editor window’ inside the MATLAB which can be accessed by selecting the ‘New Script’ button in the top panel. This window allows you to write, edit, create, save and access files from the current directory of MATLAB. You can, however, use any text editor to carry out these tasks. On most systems, MATLAB provides its own built-in editor. From within MATLAB, terminal commands can be typed at the MATLAB prompt following the exclamation character (!). The exclamation character prompts MATLAB to return the control temporarily to the local operating system, which executes the command following the character. After the editing is completed, the control is returned to MATLAB. For example, on UNIX systems, typing the following commands at the MATLAB prompt (and hitting the return key at the end) invokes the vi editor on the

Emacs editor.

!vi myprogram.m % or

!emacs myprogram.m

Note that the ‘%’ symbol is used for commenting in MATLAB. Any command that is preceded by this simple will be ignored by the interpreter and not be executed.

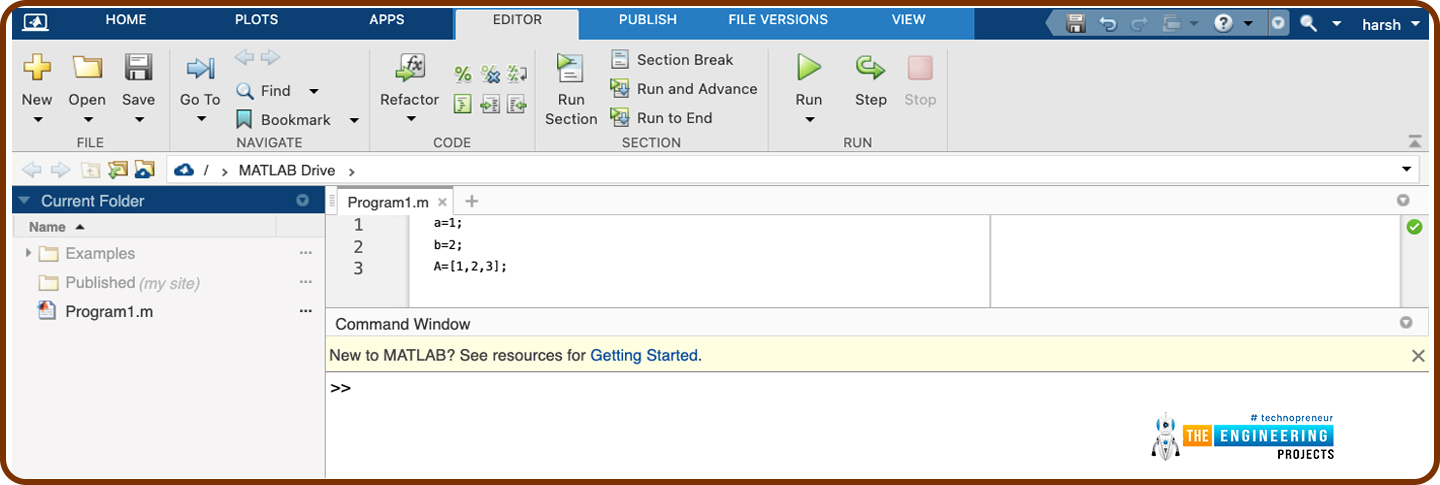
In the figure above, we have saved our very first program titled ‘Program1.m’ using the editor window in MATLAB.

Since MATLAB is for scientists and engineers primarily, it directly understands a lot of mathematical numbers natively, such as pi, e, j (imaginary number) etc.

You can quickly go to the MATLAB or the Octave terminal to test this out. Just type pi, or e and press enter to see what you get.

Introduction to Simulink

MATLAB is also a great simulation software. For more sophisticated applications, MATLAB also offers SIMULINK which is an inbuilt simulation software and provides a block diagram environment for multidomain simulation and Model-Based Design. Simulink provides a graphical editor, customizable block libraries, and solvers for modelling and simulating dynamic systems.

A very simple example of the Simulink block diagram model can be understood by the following model which simply adds or subtracts two or more numbers.

The block diagram looks as follows:

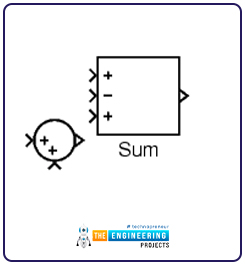
The model example for this can be opened using the following command.

openExample('simulink/SumBlockReordersInputsExample')

You can start playing with this model at once, on your MATLAB Desktop. And in fact you will find many more such examples of modelling and simulation programs that you can already start playing with online, in the set of MATLAB examples and also on the forum.

The MATLAB Community and Forum

MATLAB provides a whole community known as MATLAB-Central where MATLAB enthusiasts can ask questions and a lot of enthusiasts are willing to answer these forum questions.

There is also also, ‘file-exchange’ which is part of MATLAB-Central where people post their programs, functions and simulations for anyone to use for free.

MATLAB provides on-line help for all of its built­ in functions and programming language constructs. The commands lookfor, help, helpwin, and helpdesk provide on-line help directly from the MATLAB prompt.

Introduction to MATLAB Toolboxes

There are also several optional "toolboxes" available from the developers of MATLAB. These toolboxes are collections of functions written for special appli­cations such as symbolic computation, image processing, statistics, control system design, and neural networks. The list of toolboxes keeps growing with time. There are now more than 50 such toolboxes. The real benefit of using MATLAB is that there are teams of engineers and scientists from different fields working on each of these toolboxes and these will help you quickly get started into any field, after understanding the basics of the language. A lot of functions that are frequently performed in any particular research field, will be at the tips of your fingers in the form of ready-to-use functions. This will help you gain essential intuitions about all the different fields you may be interested in learning, getting started on, and quickly becoming a pro in. That’s the unique power MATLAB users wield.

Over the coming tutorials, we will look at the wonders that can be performed with MATLAB.

MATLAB can also interface with devices, whether they are GPIB, RS232, USB, or over a Wi-Fi, including your personal devices. It can help you manipulate images, sound and what not! You can also do 3d manipulation of animated models in MATLAB, and that’s very easy to do. We will go over this as well. We will also look one level below these 3d models and see how these themselves are also just numbers and coordinates in the end.

I absolutely enjoy MATLAB, and there’s a simple reason I’m presenting this tutorial series to you. Because I believe you should enjoy it too!

This will not only let you see ‘The Matrix’, which is the way computers perceive the real world around us, it will also change the way you yourself look at the world around you, and maybe you eventually start asking the holy question yourself… “Are we all living in a simulation?”

Exercises

Exercise: While you can get started on your own with the forum, and functions and simulations freely available, in order to procedurally be able to follow our tutorial and be able to build everything on your own from the scratch, we will strongly recommend you to follow our exercise modules.

In today’s module, we will ask you to perform very basic arithmetic tasks that will give you an intuitive feel of how to use the MATLAB prompt as an advanced calculator and make the best use of it.

For this we recommend finishing the following tasks:

1. Use the following arithmetic operations to carry out complex calculations between any two numbers. The arithmetic operations are: Addition (+), subtraction (-), multiplication (*), division (/), and power(^).
2. Also try to use basic math functions that are built-in for MATLAB such as, exp, log, sin, cos, tan, etc. Here are a few examples of commans you can run

sin(pi/2) exp(4)

log(10)/log(3)

3. Also, define a few variables. Not only number variables, but also matrix variables as shown in the example below.

a=1; b= 2; c = 3; A= [1,2,3,4]; B= [5,6,7,8];

Notice that the case-sensitivity does matter for the name of the variables.

Pro Tip: You can also perform the arithmetic operations of addition, subtraction, multiplication, division and power, element-wise between any two matrices. While addition and subtraction work element-wise by default, you can perform element-wise multiplication, division, and power by using the arithmetic operations as ‘.*’, ‘./’ and ‘.^’

In the next tutorial, we will deep dive on the data types of MATLAB, keywords, what functions mean, and also write our very first function in MATLAB. If you are familiar with loops, that may come easy, because we will also write our very first loop that will help us perform repeated tasks with a relatively small number of commands.