Arithmetic Operators in Python
- Arithmetic operators ( +, -, *, /, ^ etc. ) are used to perform simple arithmetic operations in python.
- So, let's open up your PyCharm and perform a simple task using these operators, as shown in below figure:
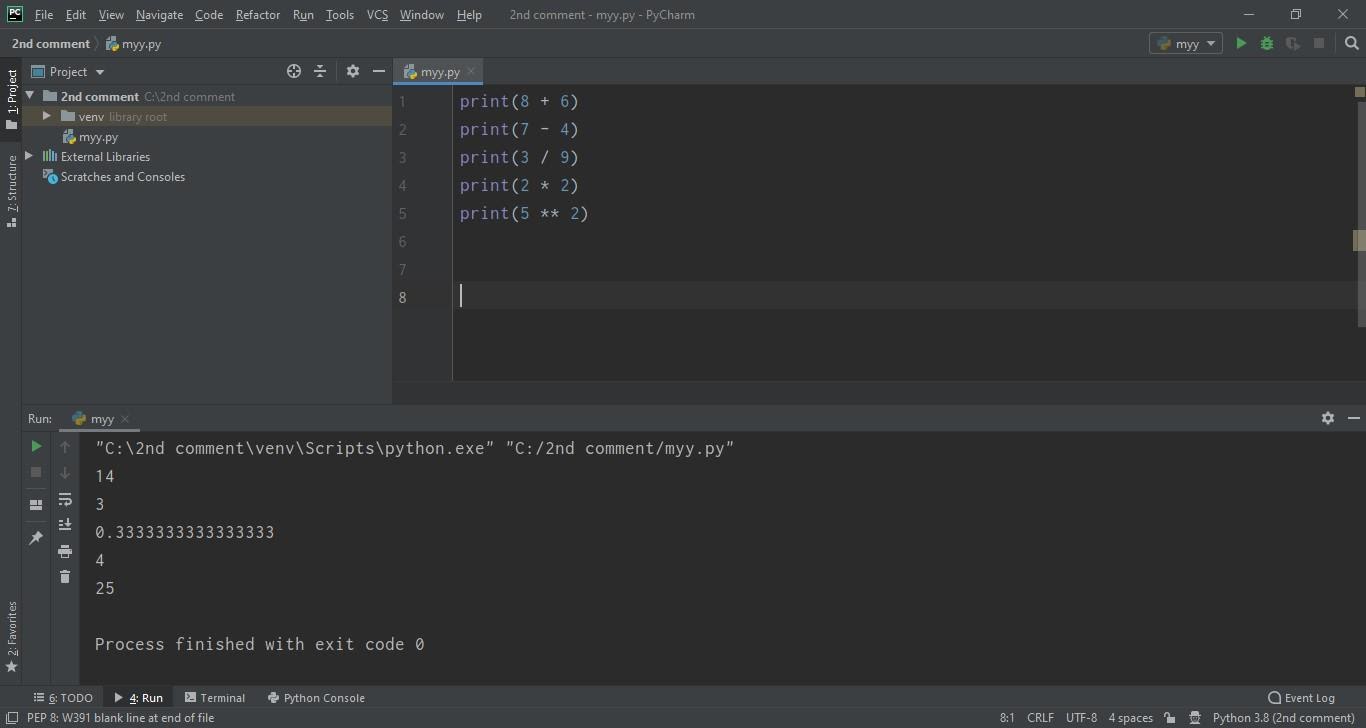
- I used a single star for multiplication and a double star for the square power.
- It is showing the results of the operations, which it is performing respectively.
Getting Input from users in Python
- If we want to work dynamically, we will learn how we get values from users.
- It quite simple in python, you will just need to use an input method here.
- It will take input from the user and store it in the assigned variable.
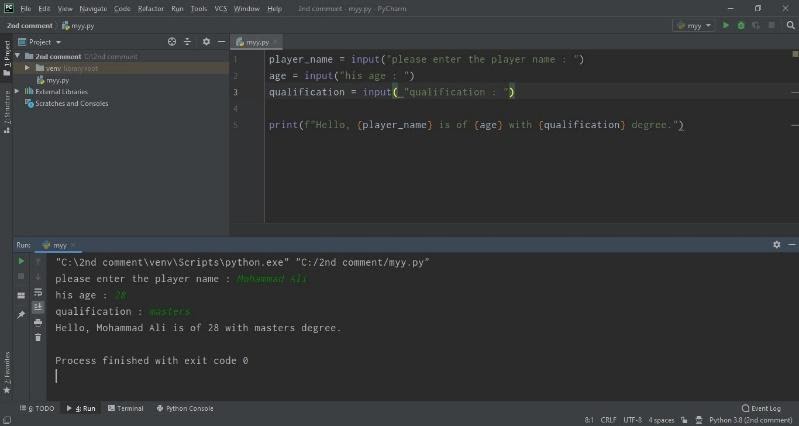
- If you want to take the full name, age, and qualification of the player, you will write it as shown in the image:
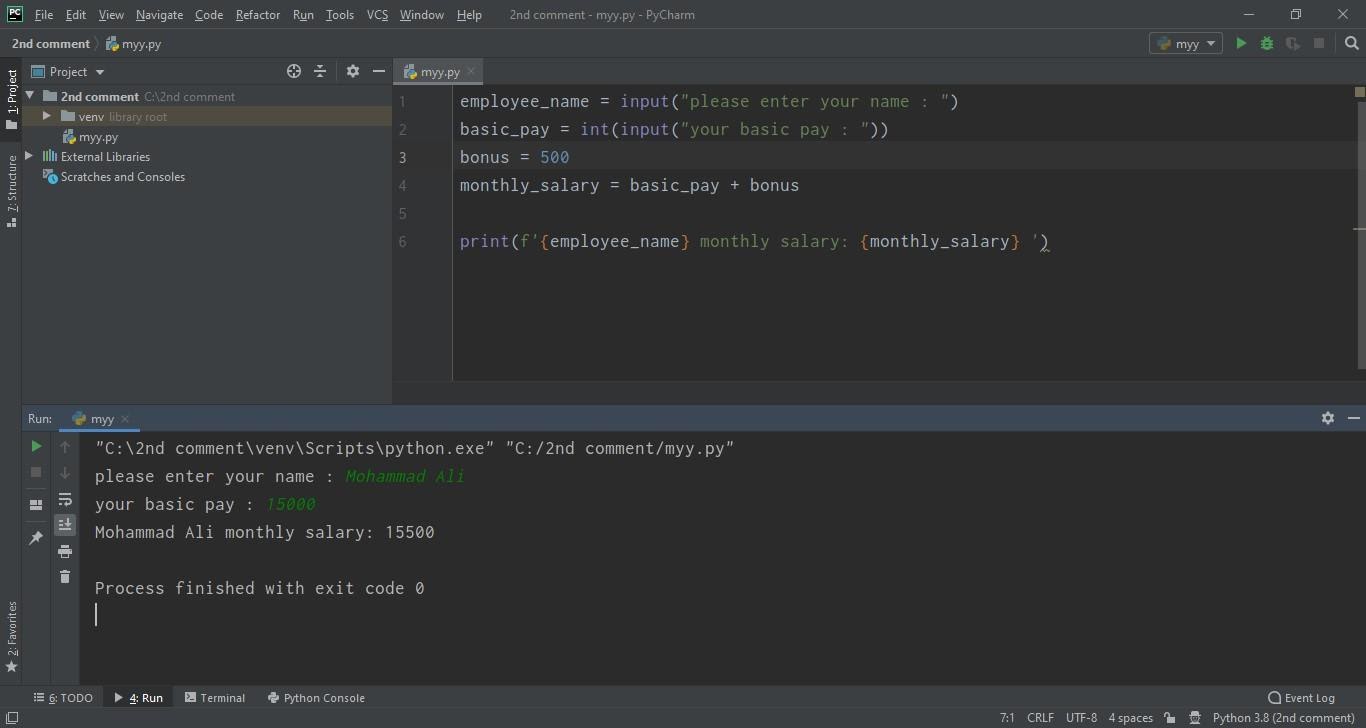
- Suppose we want to count the salary of an employee. See the steps in the image.
- Here I put int. before the fourth string, which is basic pay, but I have put the bonus in the whole numbers and it will be unable to do the concatenation because it is allowing it as a string. So, I typed the data and run it, see the results.
- You can also use the second method as you can put int. where you are performing calculations, as shown in the image.
- You can convert it by using three major data types i.e. int, float, string.
Simple Calculator in Python
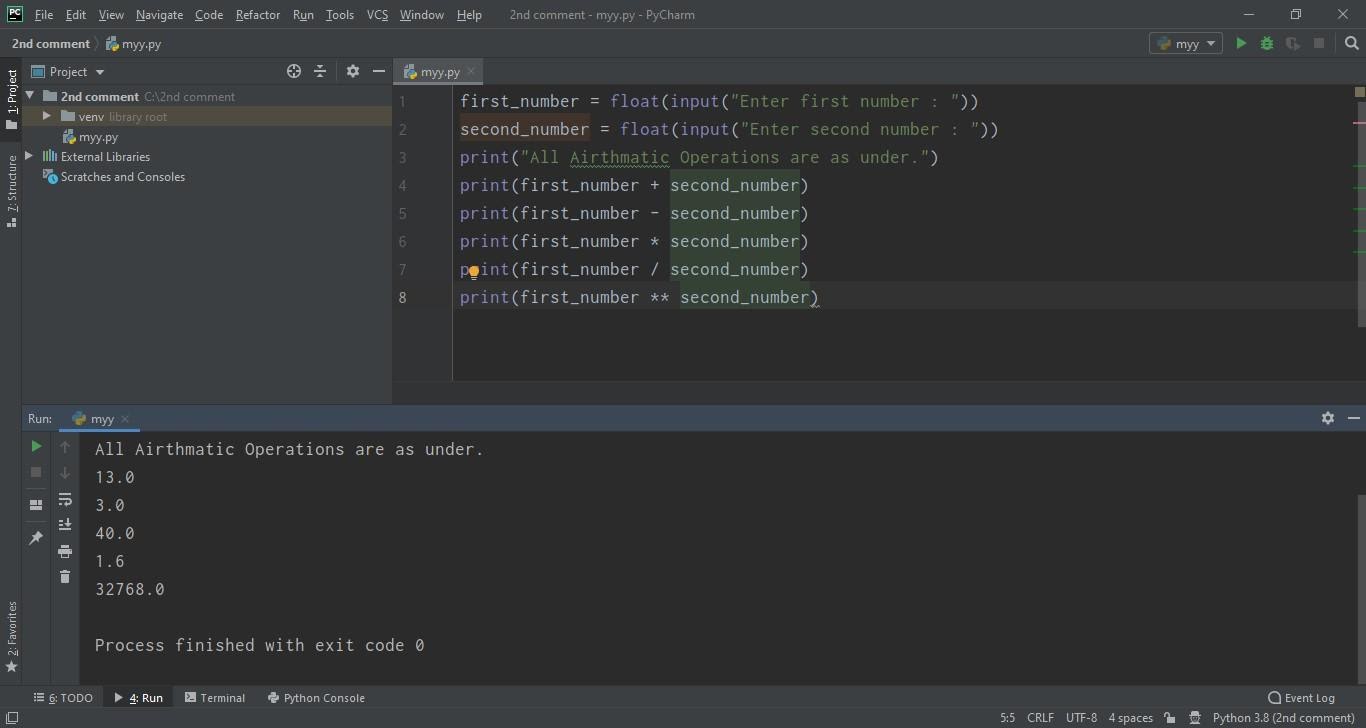
Now we will design a simple calculator in which the user will enter 1st & 2nd number and our code will perform these operations with those operators like addition, subtraction, division, and multiplications. I typed the following strings below:- first_number = float(input("Enter first number : "))
- second_number = float(input("Enter second number : "))
- print("All Arithmetic Operations are as under.")
- print(first_number + second_number)
- print(first_number - second_number)
- print(first_number * second_number)
- print(first_number / second_number)
- print(first_number ** second_number)
- I converted the type of first and second strings.
- Run the program
- You can see in the printed screen all the arithmetic operations are performed respectively.
- All the values are in floating points because we converted it into the float.
- You can also convert it in integer and check it.
- I wrote 9 and 5 and enter it, results are shown in above figure.
Operator Precedence in Python
Let's suppose, we have a variable here.- Profit = 15 + 30 * 25
- Now let's print it using: print(profit)
- Run the program.
- The answer will be 765 in the output window.
- Suppose, we want to operate the addition method first.
- So, I will place parenthesis before and after both terms.
- Then it will perform the addition method first then multiplication.
- I will write it as:
profit = (15 + 30) * 25
- Run the program and answer will be 1125.
profit = (15 + 30) * 25 - 10
- Run the program and answer will be 1115.
- If we add parenthesis to it as:
profit = (15 + 30) * (25 - 10)
- Run the program and we will get 675.
- Suppose we have a variable as, number = 3.7.
- I want easily round it using:
print(round(number))
- Run the program and it will round the figure to 4.
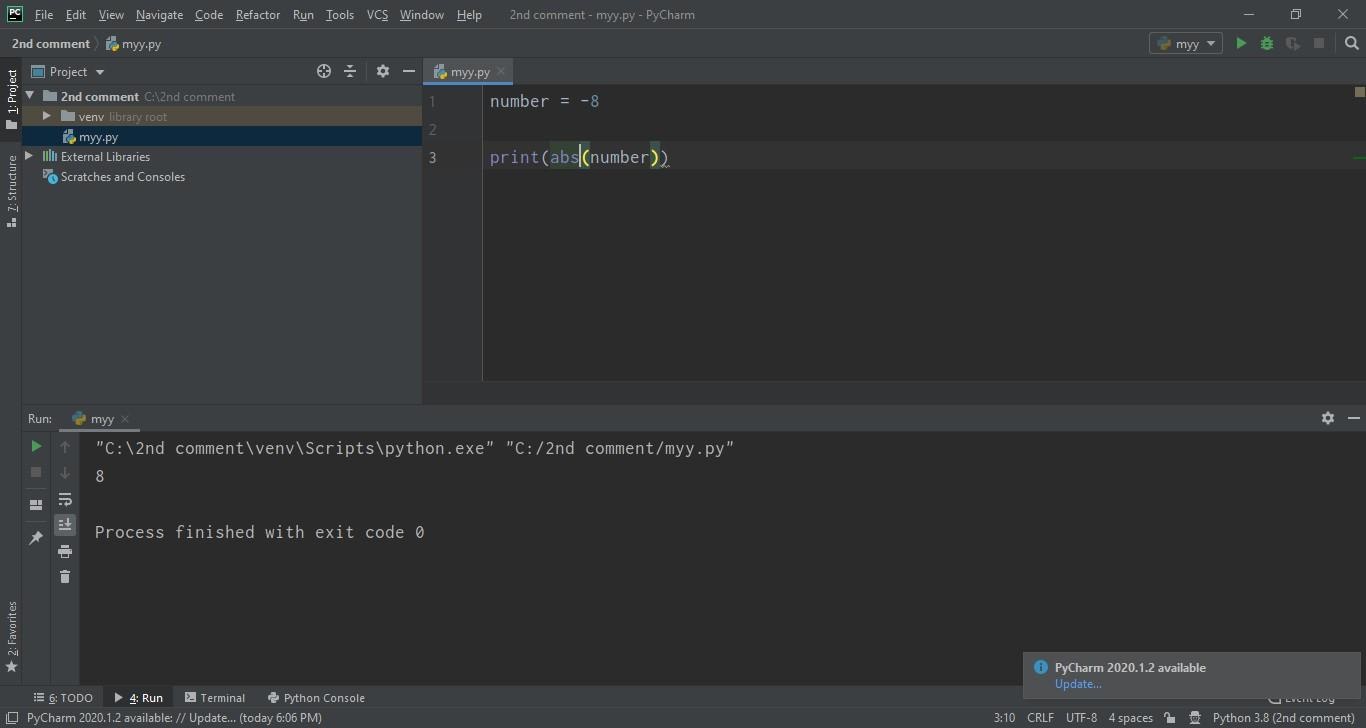
- Suppose I have negative value -8 and I want to find the absolute value of it.
- I will use abs() and it It will return 8, as shown in below figure:

- If I want to find the minimum value among the two numbers. I will write it as:
print(min(9, 4.5)
- It will return the minimum value as, 4.5.
- You can do the exact opposite of min, if you want to find out the maximum value among the two numbers.
print(max(9, 4.5)
pow()- If I want to calculate the multiples of itself i.e. square, cube etc. then I will write it as:
print(pow(5, 3)
- The first number will be base and the second one will be the power.
- Run the program & it will show the answer, 125.
Import a Math Module in Python
Now let's have a look at How to import a math module in python code:- Python Math library has a lot of builtin functions, which we can easily import by writing this statement at the top of our code.
from Math import *
- By writing this statement we are simply saying that get access to all the functions of Math Library.
- Suppose I want to take the square root of number = 72
- I write it as
print (sqrt(number))
- Run the program and it will return as 8.4 something, as shown in below figure:
| Function | Description |
|---|---|
| ceil(x) | It returns the previous integer value. |
| copysign(x, y) | It will assign sign of y to x. |
| fabs(x) | It returns the absolute value. |
| factorial(x) | It returns the factorial value. |
| floor(x) | It returns the next integer value. |
| fmod(x, y) | It divides x by y and returns the remainder. |
| frexp(x) | It returns the mantissa and exponent as pair value. |
| fsum(iterable) | It returns an accurate floating point sum of values in the iterable |
| isfinite(x) | It returns TRUE, if the number is finite i.e. neither infinite nor NaN. |
| isinf(x) | It returns TRUE, if the number is infinite. |
| isnan(x) | It returns TRUE, if the number is NAN. |
| ldexp(x, i) | It returns x * (2**i). |
| modf(x) | It returns the fractional and integer values. |
| trunc(x) | It returns the truncated integer value. |
| exp(x) | It returns e**x |
| expm1(x) | It returns e**x - 1 |
| log(x[, base]) | It returns the logarithmic value to the base e. |
| log1p(x) | It returns the natural logarithmic value of 1+x. |
| log2(x) | It returns the base-2 logarithmic value. |
| log10(x) | It returns the base-10 logarithmic value. |
| pow(x, y) | It returns x raised to the power y. |
| sqrt(x) | It returns the square root of x. |
| acos(x) | It returns the arc cosine of x. |
| asin(x) | Returns the arc sine of x. |
| atan(x) | Returns the arc tangent of x. |
| atan2(y, x) | Returns atan(y / x) |
| cos(x) | Returns the cosine of x |
| hypot(x, y) | Returns the Euclidean norm, sqrt(x*x + y*y) |
| sin(x) | Returns the sine of x |
| tan(x) | Returns the tangent of x |
| degrees(x) | Converts angle x from radians to degrees |
| radians(x) | Converts angle x from degrees to radians |
| acosh(x) | Returns the inverse hyperbolic cosine of x |
| asinh(x) | Returns the inverse hyperbolic sine of x |
| atanh(x) | Returns the inverse hyperbolic tangent of x |
| cosh(x) | Returns the hyperbolic cosine of x |
| sinh(x) | Returns the hyperbolic cosine of x |
| tanh(x) | Returns the hyperbolic tangent of x |
| erf(x) | Returns the error function at x |
| erfc(x) | Returns the complementary error function at x |
| gamma(x) | Returns the Gamma function at x |
| lgamma(x) | Returns the natural logarithm of the absolute value of the Gamma function at x |
| pi | Mathematical constant, the ratio of circumference of a circle to it's diameter (3.14159...) |
| e | mathematical constant e (2.71828...) |



 Python
Python ayeshayounas
ayeshayounas 0 Comments
0 Comments


















 2.3k
2.3k
 953
953
 921
921
 2.1K
2.1K

