Hey, learners! Welcome to the next tutorial on Python with examples. We have been working with the collection of elements in different ways, and in the previous lecture, the topic was the built-in functions that were used with the sets in different ways. In the present lecture, we will pay heed to the basic operations of the set and their working in particular ways. We are making sure that each and every example is taken simply and easily, but the explanation is so clear that every user understands the concept and, at the same time, learns a new concept without any difficulty. The discussion will start after this short introduction of topics:
How do we declare and then find the difference between the two sets?
What are the built-in functions for operations, and how do we use them in the codes?
How do we apply the operation of symmetric differences on the sets?
What is chaining in iteration, and how do we use it? Give some examples.
How do you define the union of the sets?
What is an intersection and how it is related to the sets?
What is the procedure to find whether the sets are equal or not? Give us some examples in Python.
All of these are important interview questions, and we are using the concept in this lesson to find the answer to each question in detail. The Jupyter notebook is being used for practical work. To open it, go to the search bar in Windows and search for the Jupyter notebook. After that, go to the “new” dialogue box and start Python 3 to create a new notebook.
Why Mathematical Operations are useful in Coding?
We all come from a programming background, and it is not surprising to know that different mathematical operations are used in programming to do useful tasks. In this lecture, you will learn the importance of mathematical functions with regard to sets. We have been working on the set since the last two lectures, and we are now aware of the details of working on sets. But during the programming process, the code contains different types of calculations, and large programs are extremely difficult to run without the involvement of mathematical operations. We will explain this with the help of different examples, and this is going to be fun because these concepts have been studied by us since our early education, and now is the time to know the reasons for that study.
Difference Between Two Sets
This is the simplest set operation and it involves the difference between the elements of the set in their corresponding values. In simple words, if we are dealing with two sets named A and B then the difference between them is a new set containing all the elements that are in set A but not in set B. In Python, there are two ways to get the difference of the set in two ways:
The difference using the sign
The difference using the function
Both of these are discussed in detail here. The difference with the sign is simple as we minus the values in the simple mathematical question. A minus sign is used between the names of the set, and we get the result.
On the other hand, if we talk about the function, Python has a built-in function that calculates the difference, and it is a more professional way to use the functions for such operations. These two methods are simply described in the example given next:
#Declaring two sets
A={12,8,34,5,90,3,2}
B={1,7,90,33,2,1,5}
#Using both methods of difference
differenceWithSign=A-B
differenceWithFunction=(A.difference(B))
#Printing results
print("A-B= ",differenceWithSign)
print("Difference with function= ", differenceWithFunction)

It is obvious that both methods give us the same results. So it totally depends on the programmer to choose the method, but here is a reminder that the order of the names of sets is important here because if we write B-A then the results will be entirely different.
Set Symmetric Difference
If you found the difference between the sets easy then you will find it more interesting because it is similar to the difference of the set but the only change is, in the resultant set, the uncommon elements of set A and B both are included instead of only the first set. In this way, the output of the entries from both the sets and no set is ignored. To denote the symmetric difference, the “^” sign is used. By the same token, the function for the symmetric difference also exists in Python,n and the keyword “symmetric_difference” is used for this. Have a look at the code and output for this case:
#Declaring two sets
A={12,8,34,5,90,3,2}
B={1,7,90,33,2,1,5}
#Using both methods of symmetric difference
SymmetricDifferenceWithSign=A^B
SymmetricDifferenceWithFunction=(A.symmetric_difference(B))
#Printing results
print("A^B= ",SymmetricDifferenceWithSign)
print("Difference with function= ", SymmetricDifferenceWithFunction)

Compare the results with the previous operation, and the difference will be clear.
Chain with Sets
In the previous lecture, we have been working with the itertools. The current case is to check whether the itertool works with the sets or not. You will see that the union of the two sets has the same results as the chain of the two sets, but for the sake of learning, we are working on both concepts. Hence, have a look at the code and understand it. After that, type the code on your own and check the results.
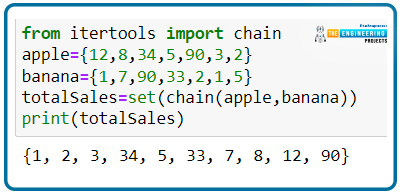
from itertools import chain
apple={12,8,34,5,90,3,2}
banana={1,7,90,33,2,1,5}
totalSales=set(chain(apple,banana))
print(totalSales)
By simply declaring and using the sets in a chain format, we are getting the result of the sales of both fruits, but in the cases where both sales were equal, the entry is ignored as we are using the set that ignores the duplicates.
At the simplest level, the results of union and chain are the same, but at a higher level, the working of both of these is different; therefore, it is important to understand both concepts and practice them with the sets.
Now, let us show you an interesting example of the same function where a set is used with the string entries. When applying the chain to that particular set, the same alphabets are ignored. The programmers can represent the results as joining or separate results, and this is explained well with the following code:
from itertools import chain
A = "Python"
B = "Programming"
C = "Tutorial"
output1 = set(chain(A, B, C))
print("before joining the set :", output1)
output2 = ''.join(res)
print("After joining the set :", output2)

We know the message is not conveyed in detail and therefore, it is proved that sets are more useful when dealing with numbers.
Union of the Sets
The name of this operation is self-explanatory if we have two sets named A and B, then the union of these sets means a new set that contains all the elements of set A and set B. We have read this in our mathematics classes, but here, this will be done with the help of coding. There are some special signs that are used to define the operations, just like we indicated the difference with the help of minus signs. When we talk about the union of the sets, we use the | sign for this, and Python also has the function for the union.
There is no need for long explanations for this operation, and we are simply changing the sign of the previous example and providing you with an example of how the difference and union give you entirely different results by changing just the operation.
#Declaring two sets
A={12,8,34,5,90,3,2}
B={1,7,90,33,2,1,5}
#Using both methods of Union
unionWithSign=A|B
unionWithFunction=(A.union(B))
#Printing results
print("A | B= ",unionWithSign)
print("Union with function= ", unionWithFunction)

As a result, the resultant set contains the values of both sets, but have you noticed that the resultant set has fewer values than the collection of both sets A and B? It is because we are using sets, and the values that are identical are just shown once.
The Intersection of the Sets
If you have understood the concept of the union of sets, then you must keep it in mind, and then by comparing the process of intersection, the concept of both these operations will be clear in your mind. It is because usually people seem confused between these two.
Let us take the case where we are discussing the recipes of two dishes that are chicken and fish and want to know the common ingredients to write in the list. For this, we will use the intersection of the set, and both of these will contain the name of the ingredients, which means these are the string sets. During the process of the intersection of sets "fish” and "chicken," the resultant set contains all the elements that are common in both sets, and all other entries are totally ignored. In this way, the person will be able to understand what things he needs from the same section of the store and where he has to go for more shopping. This will be done with the help of the following code:
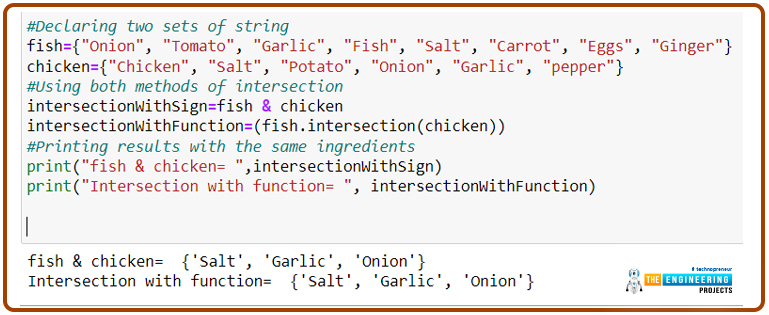
#Declaring two sets of string
fish={"Onion", "Tomato", "Garlic", "Fish", "Salt", "Carrot", "Eggs", "Ginger"}
chicken={"Chicken", "Salt", "Potato", "Onion", "Garlic", "pepper"}
#Using both methods of intersection
intersectionWithSign=fish & chicken
intersectionWithFunction=(fish.intersection(chicken))
#Printing results with the same ingredients
print("fish & chicken= ",intersectionWithSign)
print("Intersection with function= ", intersectionWithFunction)
Equality of the Sets
When dealing with different types of sets, let's say set Apple and set Banana, where the shopkeeper stores the data of the weekly sales of cartons, the seller wants to take the record of the day and check if the sales are the same or not. Then, he simply checks the results by applying the equal signs for the two times between the sets and getting the result. Keep in mind that the order of the set does not matter here as the set does not have the index values. So, no matter if the sales were not equal on the same day, if the weekly sales are matching exactly, then the sets will be equal.
#Making the set of apples and banana with the sales
apple={34,78.9,32,89.7,33,12.6,55}
banana={12.6,78.9,33,34,32,89.7,55}
#using if loop to check the results and print the output
if apple==banana:
print("Sales of apple and banana are the same")
else:
print("Sales of apple and banana are not the same")

Now, to elaborate on this more, the sets that are used in the previous examples are fed into the same code, and then by running the code, we can conclude the results.
#Making the set with the sales
apple={12,8,34,5,90,3,2}
banana={1,7,90,33,2,1,5}
#using if loop to check the results and print the output
if apple==banana:
print("Sales of apple and banana are the same")
else:
print("Sales of apple and banana are not the same")

The “if” loop is an important iteration, and this is the best way to explain how we can use it for the bi-conditional cases. These loops will soon be used in many complex codes in this tutorial.
Hence, it was a fantastic tutorial on sets, and we learned a lot with the help of different operations. We had an idea about the sets and their characteristics, but in this lecture, the operations and working of the sets are well explained, and we see the difference, symmetric difference, chain, union, intersection, and equality operations of the sets in detail. I hope you get the point that we are trying to make clear. For more interesting tutorials, stay on the same website.







































 Python
Python ayeshayounas
ayeshayounas 0 Comments
0 Comments


















 2.3k
2.3k
 953
953
 921
921
 2.1K
2.1K

