This is the next lesson in our Python course. Previously, we looked at an overview of the different data types in python such as dictionaries, Boolean and sets. This tutorial will focus on Python sets to get a deeper understanding of this data type, so let's get started. During your schooling, there is a good chance you learned about sets and set theory. Venn diagrams may even be familiar to you:
Don't worry if you don't recognize this! You should still be able to access this tutorial without any problems. Rigidly defining a set in mathematics can be both abstract and difficult to understand. A set is thought of as a well-defined group of unique objects, which are sometimes called "elements."
Python's built-in set type facilitates the grouping of items into sets, which is important in programming as well. Unique actions that can be done on a set separate it from other object types.
What will you learn?
Using Python, you learn how to create set objects and learn about the various activities they can be used for. We've covered lists and dictionaries in previous tutorials, so you should be familiar with when a set is the right tool for the job. You'll also look at "frozen sets," which are similar to sets but differ in one significant way.
What is a set?
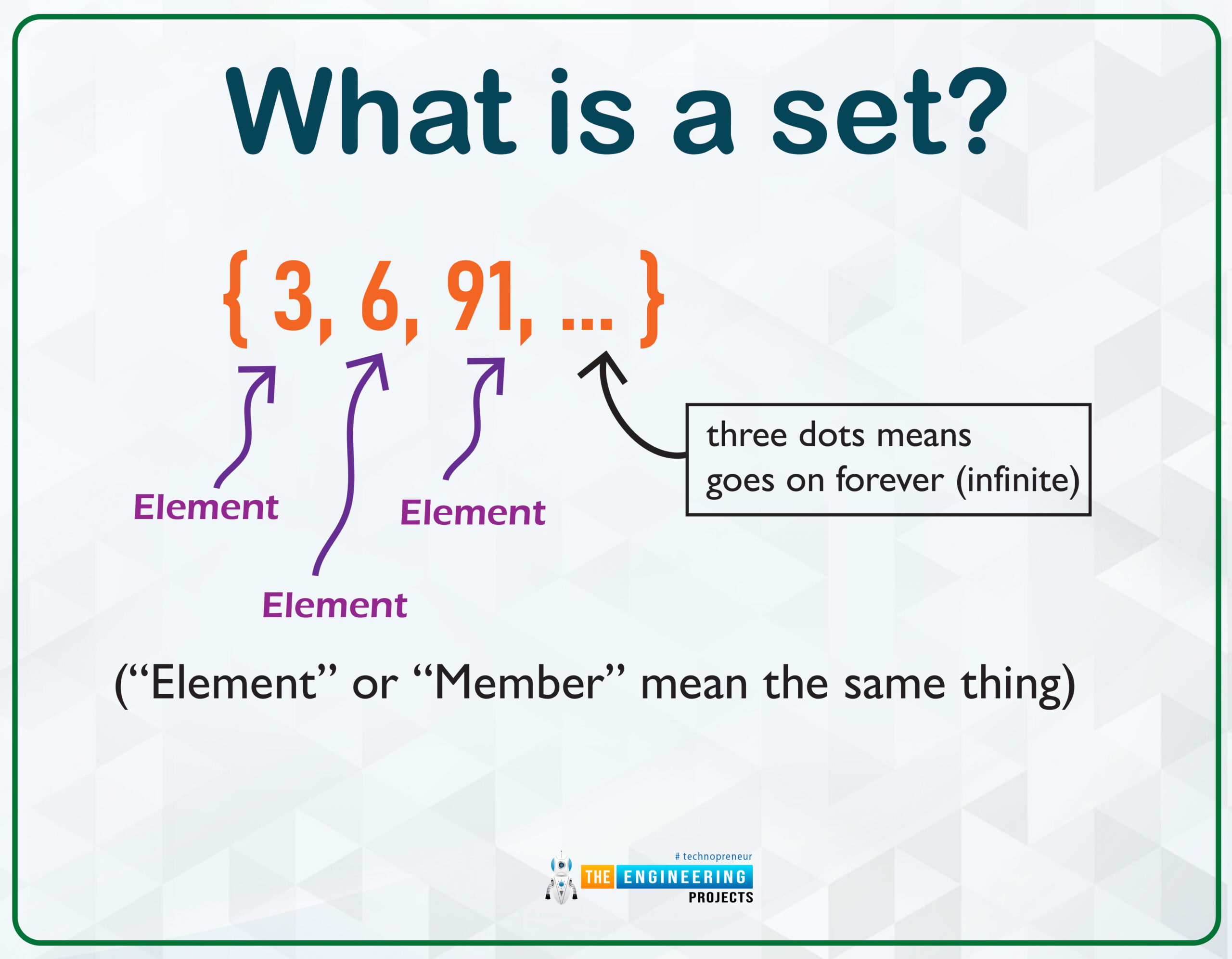
The following features describe the built-in set type in Python:
- Sets are not in any particular order.
- Each element in the set is unique. It is not permitted to use duplicate elements.
- A set's elements can be changed, but the set's elements must be immutable.
Let us explore what all that entails, and how you can interact with sets in Python.

Iter> is an iterable (imagine a list or tuple for now) that generates a list of items to be included in the set. This is the same as the list method's iter> argument .extend():

A string can also be supplied to set() because strings are iterable. As you can see, list(s) generates a list of the characters in the string s. In the same way, set(s) generates a set of the characters in s:

The resulting sets are not in any order. The definition's original order isn't always followed. Values that are duplicated such as the string 'foo' in the first two examples and the letter 'u' in the third are only represented in the set once.
Curly braces () can also be used to define a set:

Each obj> becomes a separate element of the set when defined in this way, even if it is iterable. The .append() list technique works similarly. As a result, the sets depicted above can alternatively be described as follows:

To summarize:
- set() takes an iterable as a parameter. It creates a list of things that should be included in the collection.
- Even though the items in curly brackets are iterable, they are added into the set intact.
Consider the following differences between these two definitions:

A set can be empty. The set() method is the sole way to define an empty set in Python because empty curly braces () are regarded as an empty dictionary.

In Boolean logic, an empty set is false:

What is a bool?

A Boolean variable can only have two values in general: True or False. In other words, we call a variable a Boolean variable if it can only have these two values. It's frequently used to denote an expression's Truth value. True equals 1 and False equals 0 in mathematics. In contrast to electronics, a light bulb has a high value (that is 1) when it is switched on, and vice versa.
Determine the size and composition of your group.
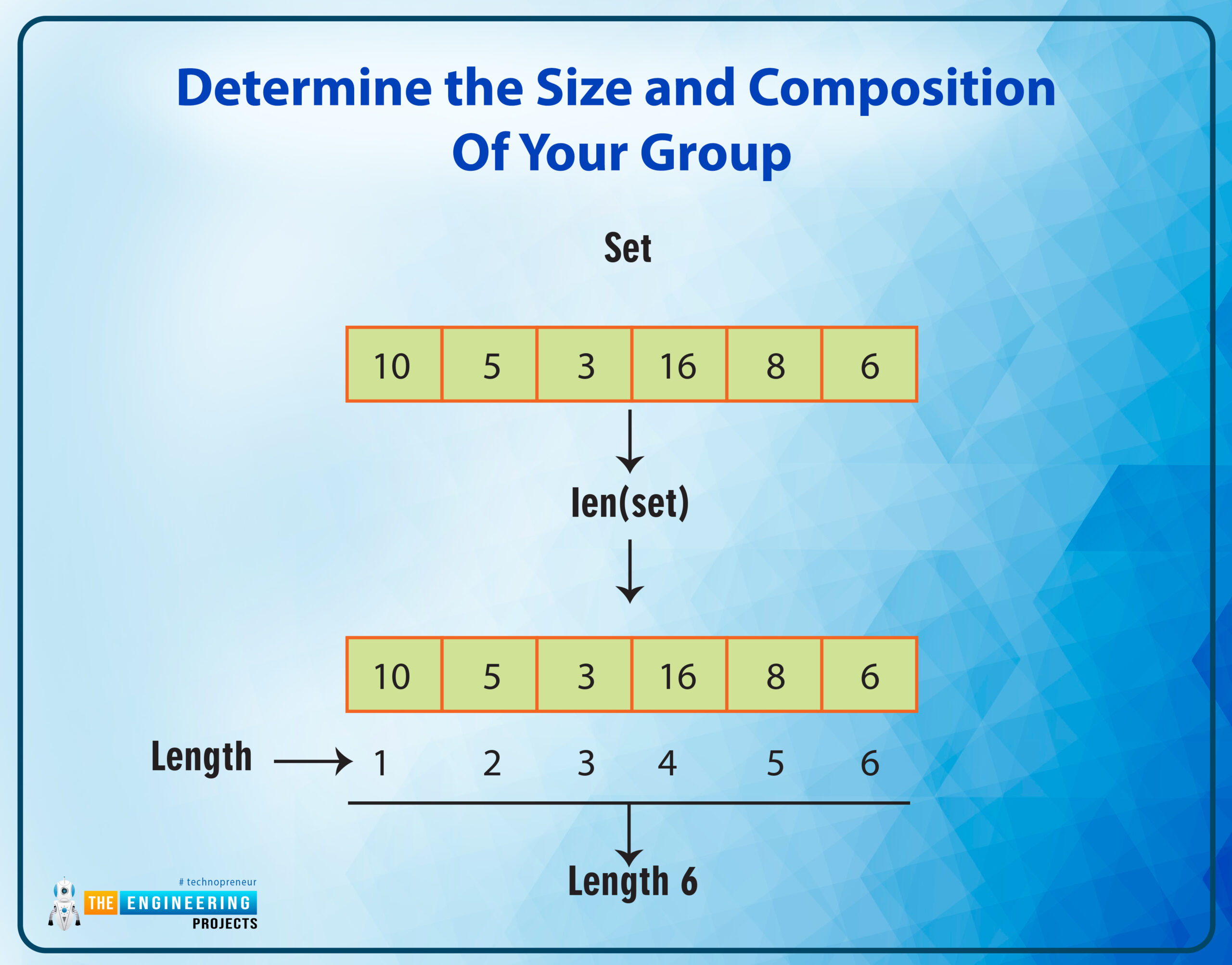
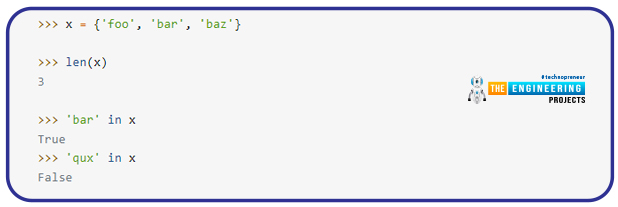
The len() function, which returns the number of items in a set, can be used to test for membership with the in and not in operators:
Working with a Set
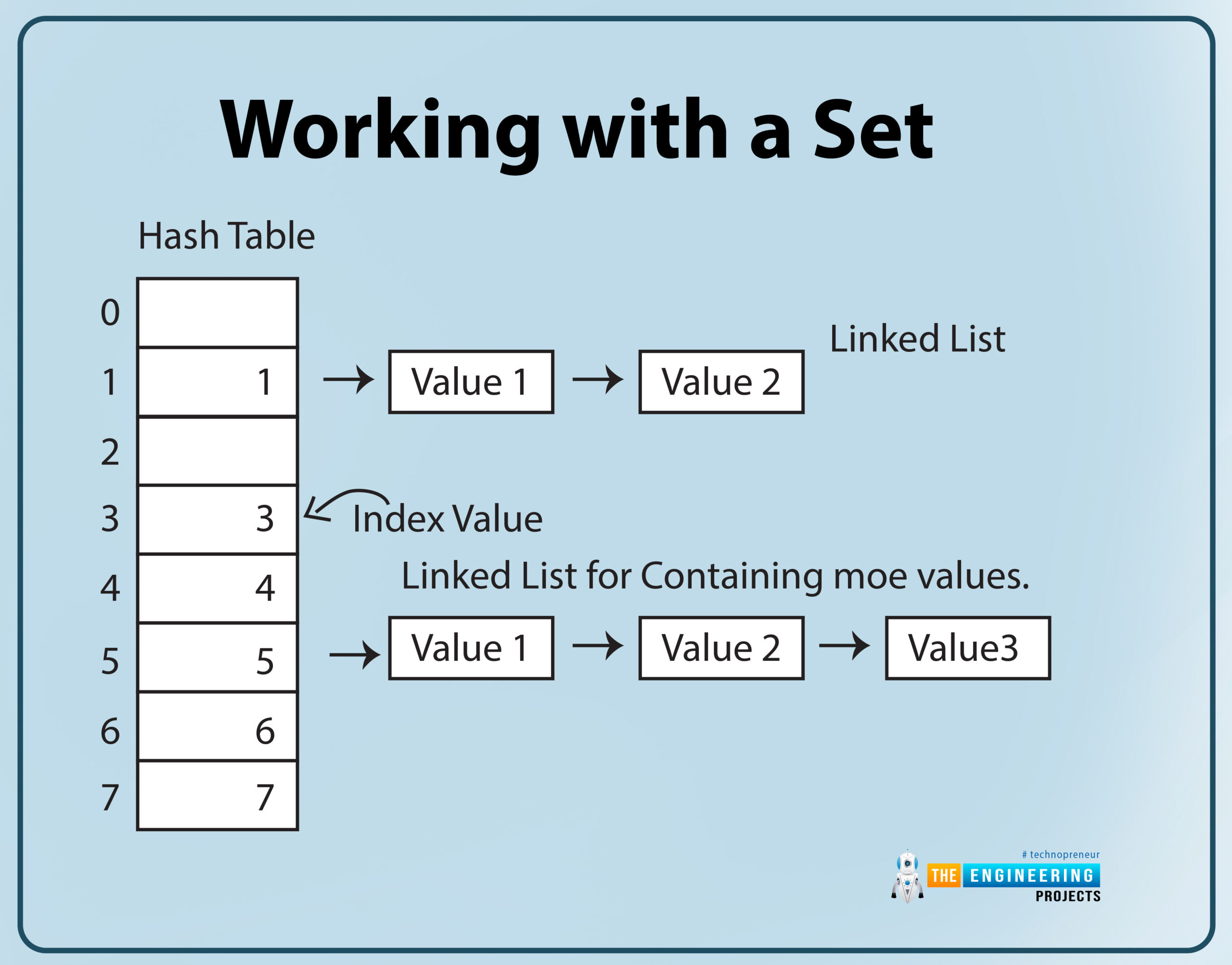
Sets are incompatible with many of the operations that operate with other composite python data types. Sets, for instance, cannot be indexed or sliced. Python, on the other hand, provides set object methods that are quite similar to the operations given for mathematical sets.
Using Operators vs. Using Methods
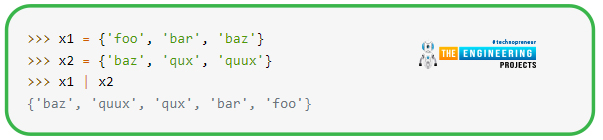
Most, but not all, set operations in Python can be accomplished using either an operator or a method. Let's look at how set union works as an illustration of how these operators and methods function. With sets, x1, and x2, the union of the two sets yields a set that contains all members from both sets.
Consider the following:

The results of combining x1 and x2 are shown below.
Note that in the union, 'baz,' will appear in both x1 and x2 only once. There are never any duplicate values in a set.
The | operator in Python can be used to execute set union:
The union() method can also be used to get a set union. The method is called using one of the sets as an input, and the other is supplied as a parameter:

The operator and method operate identically when used in the instances above. However, there is a distinction between them. Both operands must be set when using the | operator. In contrast, the union() method takes any iterable as an input, turns it into a set, and then executes the union.
Take note of the differences between the following two statements:

Both try to combine ('baz', 'qux', 'quux') with x1. The | operator fails, but the union() method succeeds.
Methods and operators that are available
A list of Python set operations is shown below. Some tasks are accomplished by an operator, while others are completed by a method, and still, others are completed by both. When a set is required, procedures normally accept any iterable as an input, whereas operators require actual sets as operands.
union
x1 | x2 [| x3 ...]
Add two or more sets together to get the unionset.
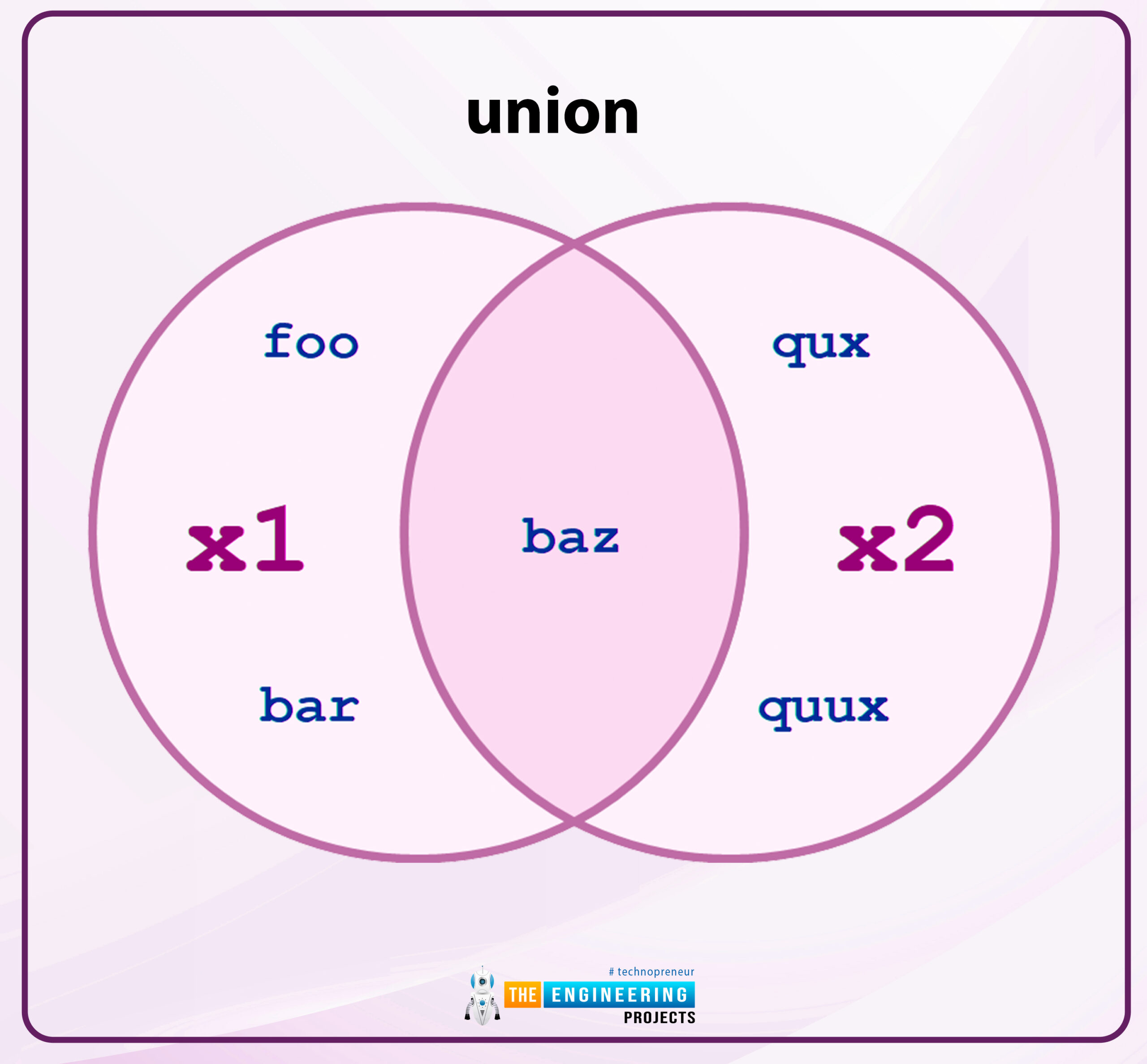
x1.union(x2) and x1 | x2: returns the sets of all items in either x1 or x2.

With either the operator or the method, you can specify more than two sets:

All elements that appear in any of the defined sets are included in the final set.
intersection
x1 & x2 [& x3 ...]
Calculate the point at where two or more sets intersect.

The set of items shared by both x1 and x2 is returned by x1.intersection(x2) and x1 & x2:

The intersection method and operator, like set union, allow you to specify multiple sets.

Only components that appear in all of the provided sets are included in the resulting set.
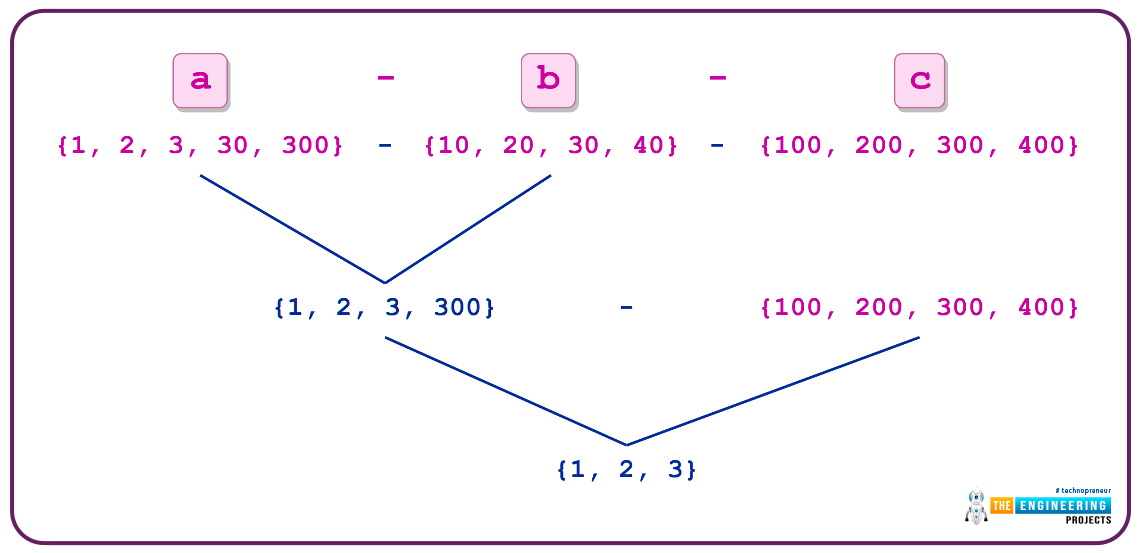
Difference
Calculate the difference between at least two sets.
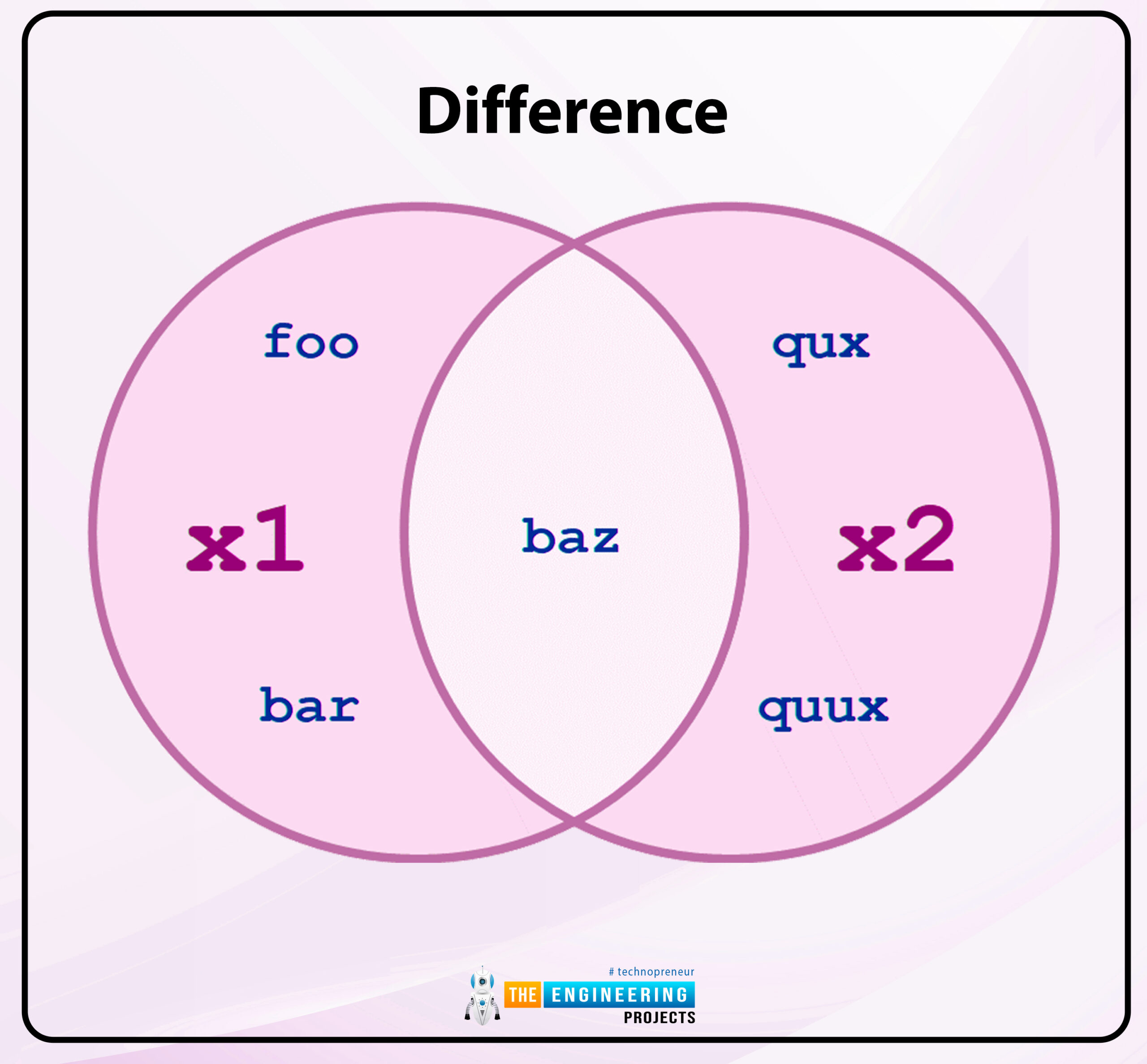
Two examples of x1.difference are x1.difference(x2) and x1 - x2 (x2). produce a list of all x1 elements that aren't found in x2:

difference(x2) and x1 - x2 return the set that is returned when any elements in x2 are removed or subtracted from x1.
You can specify multiple sets once more:

The procedure is executed from left to right when several sets are supplied. In the foregoing example, the first step is to compute a - b, which yields 1, 2, 3, 300. After that, the set is taken from c, leaving 1, 2, and 3:
Symmetric difference
Calculate the difference between two symmetric sets.

The sets containing all items in x1 or x2, but not both, are returned by symmetric difference(x2) and x1 x2:

Additionally, the operator ^ enables for more than two sets:

The operation is executed from left to right once multiple sets are supplied, just like with the difference operator.
Surprisingly, although the operator supports multiple sets, the symmetric_difference() function does not:

Making Changes to Sets
Sets can be altered, even though their components need to be immutable types. Similar to the operations above, the contents of a set can be altered using a combination of operators and processes.
Methods and Operators for Augmented Assignment

Each of the aforementioned operators has an augmented assignment form that can be used to change a set. Each person takes a different approach.
Update

x1 |= x2 [| x3 ...]
The union can be used to change the state of a set.

Intersection

x1 &= x2 [& x3 ...]
Intersection can be used to change a set.
x1 &= x2 and update(x2) x1 should be updated with only the items that present in both x1 and x2:

Difference_update
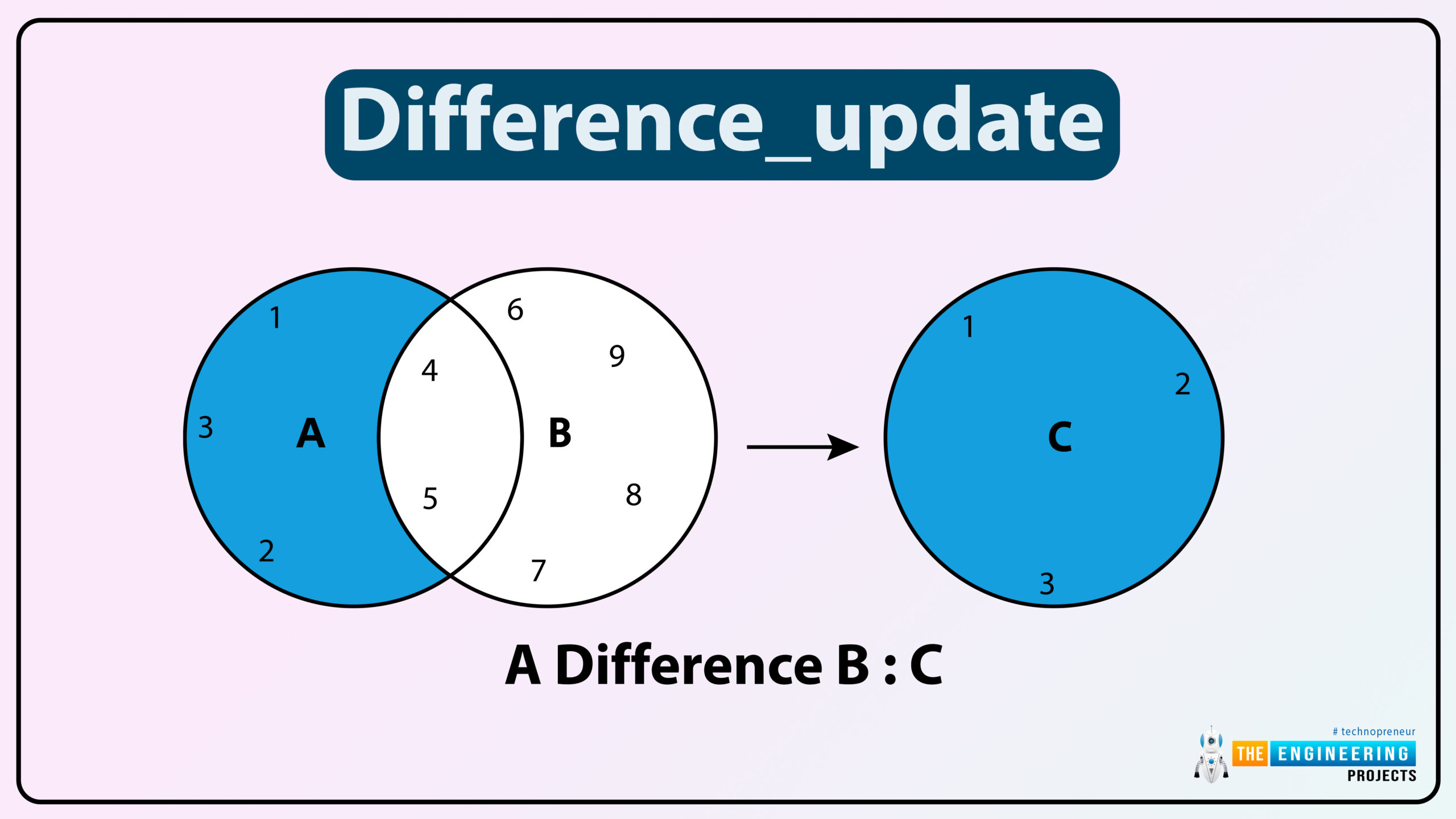
x1 -= x2 [| x3 ...]
Make a difference in a set.
x1.difference update(x2) and x1 -= x2 remove components found in x2 from x1:

Symmetric_difference_update
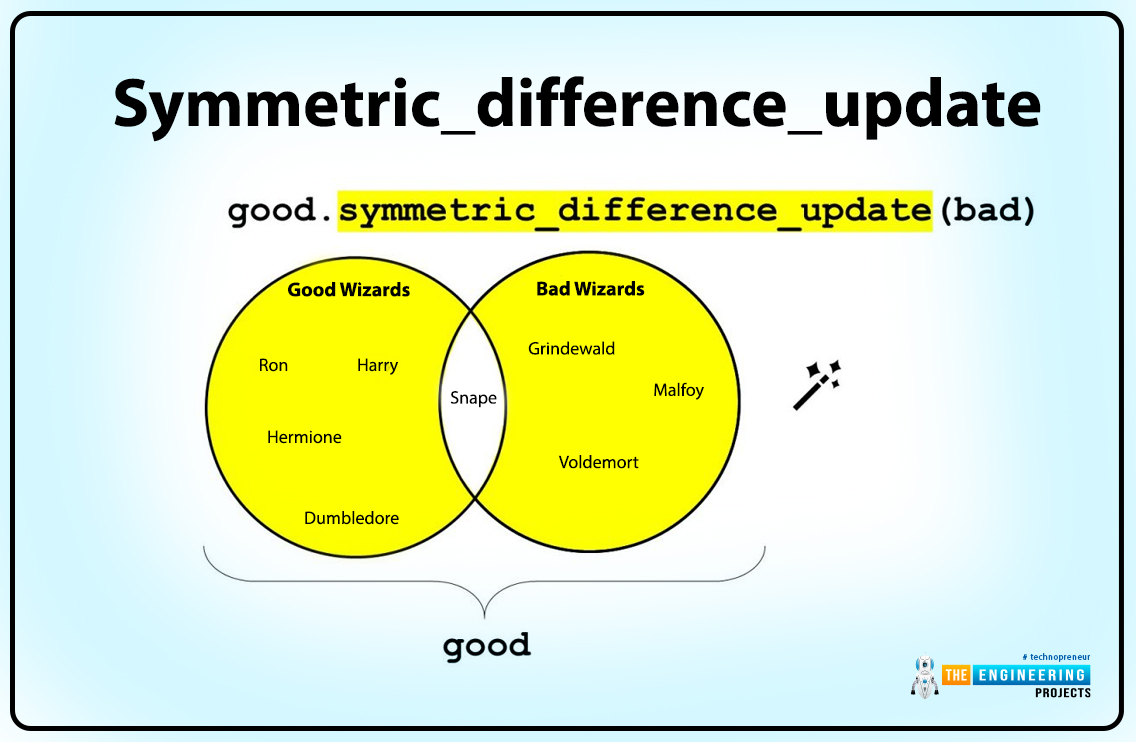
x1 ^= x2
By using symmetric difference, you can change a set.
x1=x2 and update(x2) update x1, maintaining either x1 or x2 components, but not both:

Other Set Modification Methods
Aside from the augmented operators listed above, Python has several other ways of modifying sets.
Add

Adds a new element to a collection.
x.add(elem>) appends elem> to x:

Remove
Removes one of a set's elements.
elem> is removed from x using x.remove(elem>). If elem> is not in x, Python throws an exception:

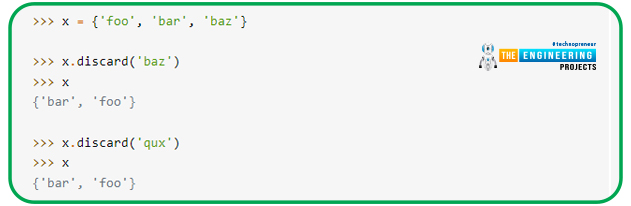
Discard
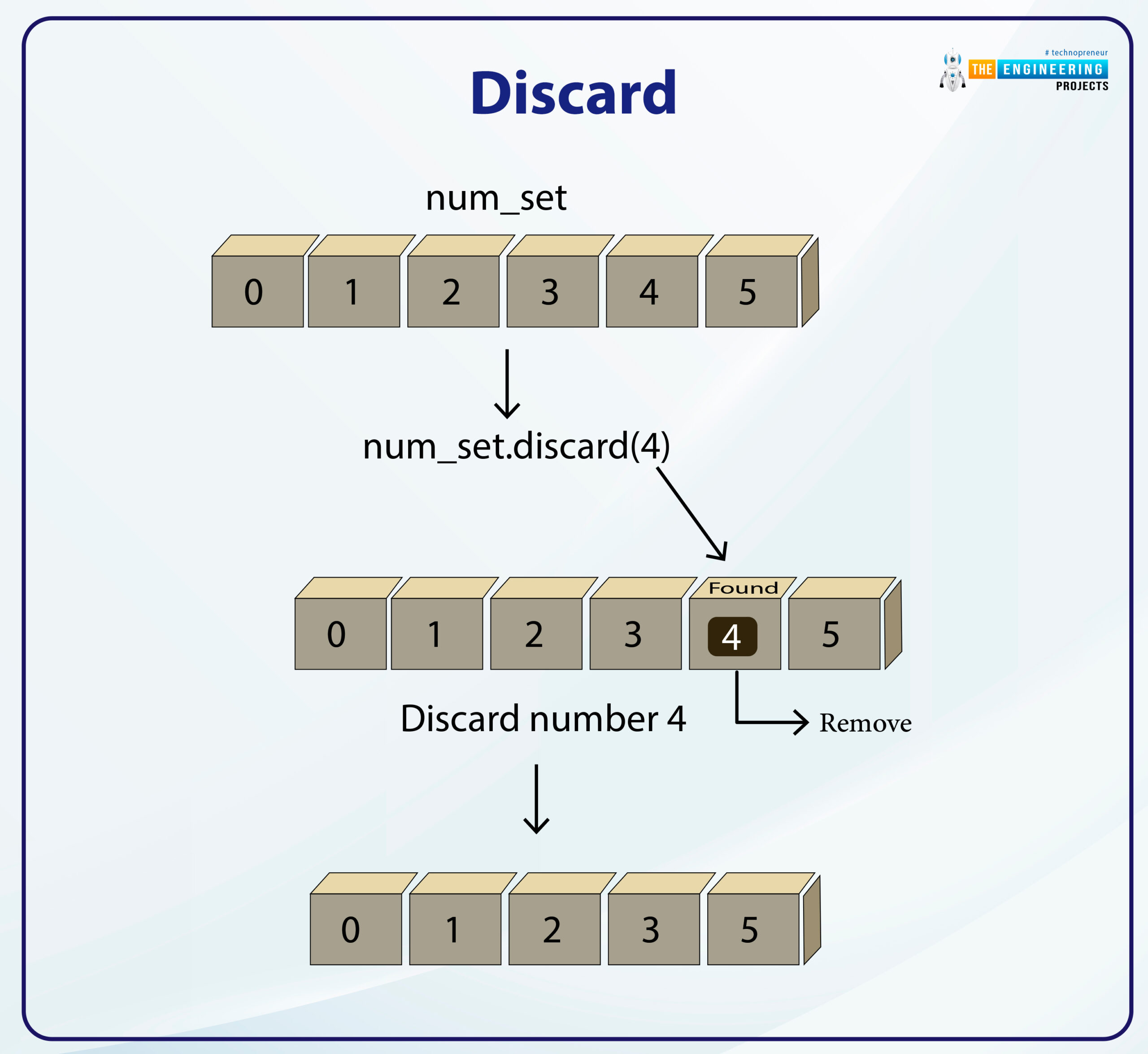
Removes one of a set's elements.
elem> is also removed by x.discard(elem>). If elem> is not in x, this procedure does nothing instead of issuing an exception:
Pop
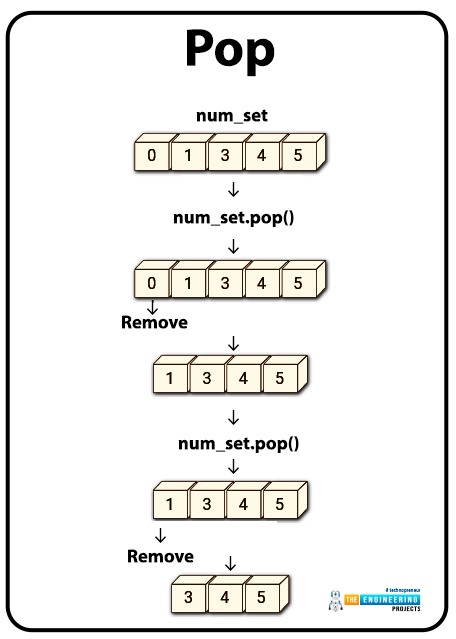
A set contains the random element to be removed from it.
x.pop() removes and returns an element from x that is picked at random. x.pop() throws an exception if x is null:

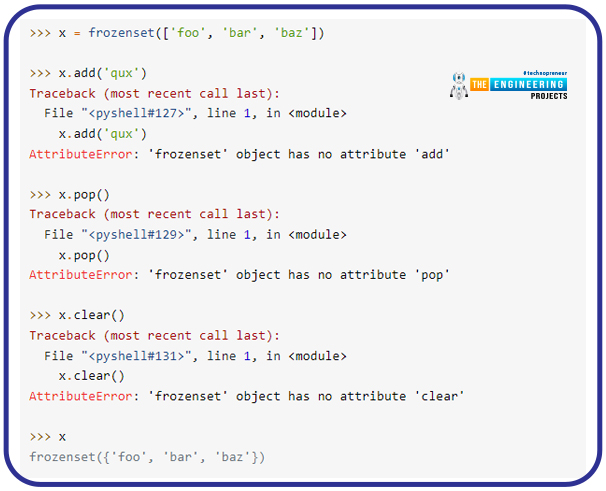
Frozen Sets
A frozenset is a Python in-built type that is similar to a set but is immutable. The following non-modifying procedures are possible on a frozenset:

Attempts to change a frozenset, on the other hand, fail:
Frozensets and Augmented Assignment: A Deep Dive
You might suppose that because a frozenset is immutable, it can't be the target of an augmented assignment operator. However, keep the following in mind:

With frozensets in place, Python does not perform augmented assignments. The expression y &= s is practically the same as y = y & s. It makes no changes to the original x. It's associating x with a new item, and the one with which it was previously connected has vanished.
The id() method can be used to check this:

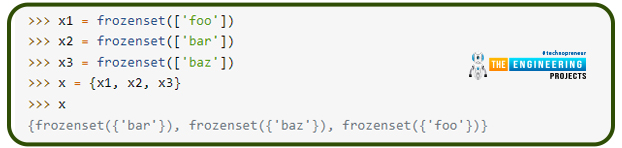
Following the augmented assignment, f has a new integer identification. It has been reassigned rather than changed in situ. When a Python object is the target of an augmented assignment operator, it is updated in place. Frozensets, on the other hand, are not. Frozensets are useful in cases where you need an immutable object yet wish to utilize a set. For example, because set elements must be immutable, a set with items that are also set cannot be defined.:

When you need to define a set of sets, frozensets, which are immutable, are the way to go:
Remember from the previous dictionary instruction that a dictionary key must be immutable. The in-built set type can't be used as a dictionary key for the following reason:

If you're looking for a way to use sets as dictionary keys, try frozensets:

How do we know if an element in a set exists?

We must use a membership operator to see if an element exists in a set. To check if an element is present in a sequence, membership operators are employed (e.g., strings, lists, tuples, sets, or dictionaries). As mentioned below, there are two membership operators.
- in: Returns True if the object on the left is contained within the object on the right.
- not in: Returns True if the left-hand item is not included in the right-hand object.
Calculating a set's length
Use the len () function to calculate the total number of items in a set. The number of items in an object is returned by this function. The function's input can be any sort of sequence, including a text, dictionary, list, or tuple, in addition to a set.
Conclusion
This tutorial teaches you how to create set objects in Python and how to interact with them using functions, operators, and methods. Python's main built-in data types should now be familiar to you. Then you'll examine the organization and structure of the code of a Python program that interacts with those items. In the next topic we will look at python list and python tuple.



 Python
Python ayeshayounas
ayeshayounas 0 Comments
0 Comments


















 2.3k
2.3k
 953
953
 921
921
 2.1K
2.1K

